Radiation of frequency is incident on two photosensitive surface and . There is no photoemission from surface . Photoemission occurs from but photoelectrons have zero kinetic energy. Explain these observation and find the value of work function for surface .
To solve the problem, we need to analyze the observations regarding the two photosensitive surfaces, P and Q, when radiation of frequency 1015 Hz is incident on them.
1. Understanding Photoelectric Effect:
The photoelectric effect states that when light of sufficient frequency strikes a photosensitive material, it can eject electrons from that material. The energy of the incident photons is given by the equation:
E=hν
where E is the energy of the photon, h is Planck's constant (6.63×10−34 J s), and ν is the frequency of the radiation.
2. Analyzing Surface P:
Since there is no photoemission from surface P, it indicates that the energy of the incident photons is less than the work function (ϕ) of surface P. Thus, we can conclude:
E<ϕP
This means that the frequency of the incident radiation is below the threshold frequency (ν0) required for photoemission from surface P.
3. Analyzing Surface Q:
For surface Q, photoemission occurs, but the photoelectrons have zero kinetic energy. This implies that the energy of the incident photons is exactly equal to the work function of surface Q. According to Einstein's photoelectric equation:
E=ϕ+KE
where KE is the kinetic energy of the emitted photoelectrons. Since KE=0 for surface Q, we have:
E=ϕQ
4. Calculating the Energy of the Incident Photons:
We can calculate the energy of the incident photons using the frequency given:
E=hν=(6.63×10−34 J s)×(1015 Hz)=6.63×10−19 J
5. Finding the Work Function for Surface Q:
Since the energy of the incident photons is equal to the work function of surface Q, we have:
ϕQ=6.63×10−19 J
6. Converting Work Function to Electron Volts:
To express the work function in electron volts (eV), we divide by the charge of an electron (1.6×10−19 C):
ϕQ=6.63×10−19 J1.6×10−19 C≈4.14 eV
Conclusion:
The work function for surface Q is approximately 4.14 eV.
The photoelectric effect states that when light of sufficient frequency strikes a photosensitive material, it can eject electrons from that material. The energy of the incident photons is given by the equation:
E=hν
where E is the energy of the photon, h is Planck's constant (6.63×10−34 J s), and ν is the frequency of the radiation.
Since there is no photoemission from surface P, it indicates that the energy of the incident photons is less than the work function (ϕ) of surface P. Thus, we can conclude:
E<ϕP
This means that the frequency of the incident radiation is below the threshold frequency (ν0) required for photoemission from surface P.
For surface Q, photoemission occurs, but the photoelectrons have zero kinetic energy. This implies that the energy of the incident photons is exactly equal to the work function of surface Q. According to Einstein's photoelectric equation:
E=ϕ+KE
where KE is the kinetic energy of the emitted photoelectrons. Since KE=0 for surface Q, we have:
E=ϕQ
We can calculate the energy of the incident photons using the frequency given:
E=hν=(6.63×10−34 J s)×(1015 Hz)=6.63×10−19 J
Since the energy of the incident photons is equal to the work function of surface Q, we have:
ϕQ=6.63×10−19 J
To express the work function in electron volts (eV), we divide by the charge of an electron (1.6×10−19 C):
ϕQ=6.63×10−19 J1.6×10−19 C≈4.14 eV
The work function for surface Q is approximately 4.14 eV.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [SET -II, OUTSIDE DELHI]
6 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [SET -III, OUTSIDE DELHI]
3 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-II DELHI BOARD (SEC-C)
4 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Fig. shows the variation of stopping potential V0 with the frequency v of the incident radiation for two photosensitive metal P and Q:
(i) Explain which metal has smaller threshold wavelength
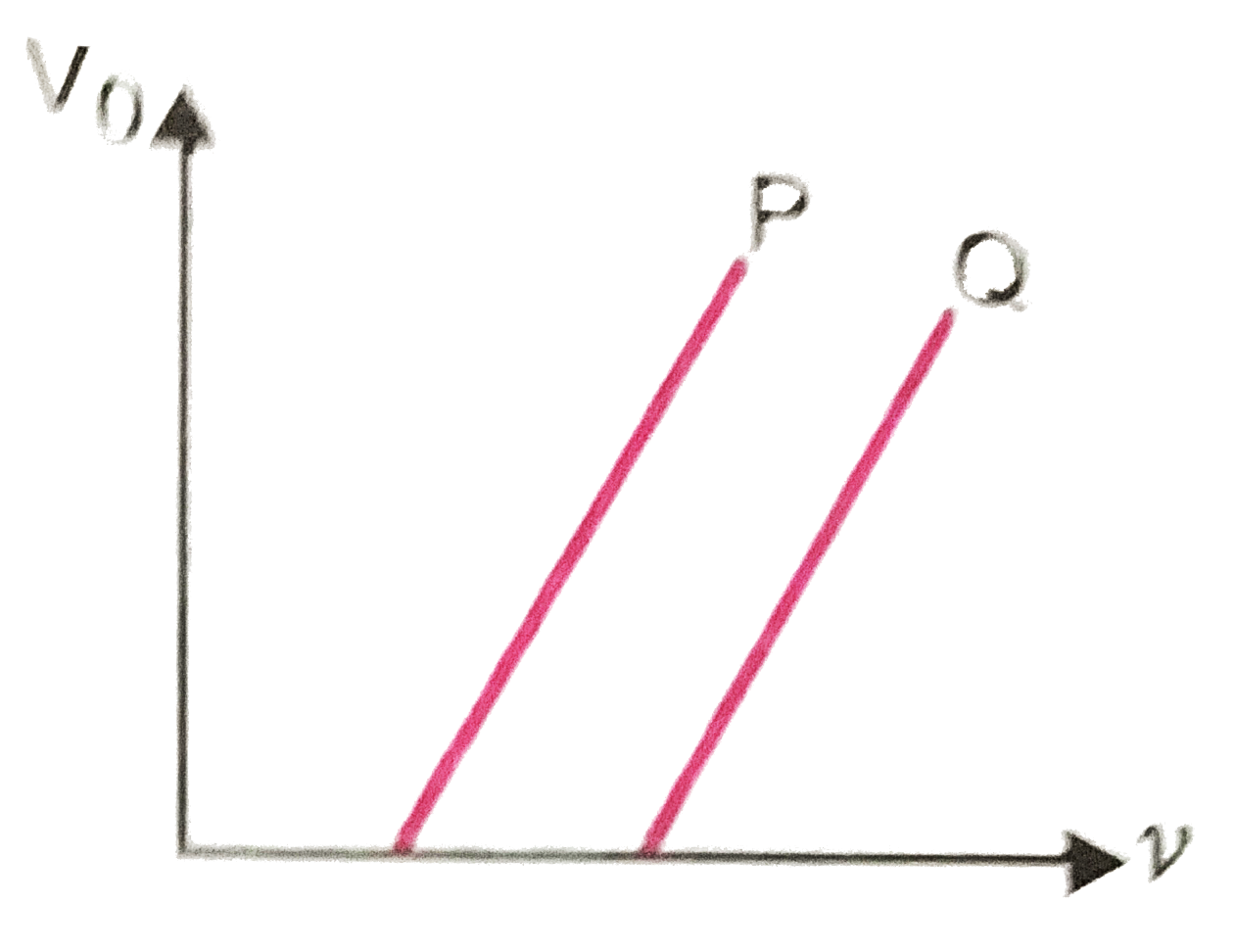
(ii) Explain, giving reason, which metal emits photoelectrons having smaller kinetic energy, for the same wavelength of incident radiation.
(iii) If the distance between the light source and metal P is doubled, how will the stopping potential change.
View SolutionIf wavelength of incident radiation changes from 500nm to 200nm then the maximum kinetic energy increases to 3 times. Find work function ?
View Solution
Knowledge Check
When the photons of energy hv fall on a photosensitive metallic surface of work function hv0, electrons are emitted are from the surface. The most energetic electron coming out of the surfece have kinetic energy equal to
AhvBhv0Chv+hv0Dhv−hv0
When light of sufficiently high frequency is incident on a metallic surface, electrons are emitted from the metallic surface. This phenomenon is called photoelectric emission. Kinetic energy of the emitted photoelectrons depends on the wavelength of incident light and is independent of the intensity of light. Number of emitted photoelectrons depends on intensity. (hv−ϕ) is the maximum kinetic energy of emitted photoelectron (where ϕ is the work function of metallic surface). Reverse effect of photo emission produces X-ray. X-ray is not deflected by electric and magnetic fields. Wavelength of a continuous X-ray depends on potential difference across the tuve. Wavelength of charasteristic X-ray depends on the atomic number.
Q. If potential difference across the tube is increased then
View SolutionRadiation of wavelength 310 nm is incidenton a metal surface of work function 1eV. Find maximum speed of photoelectrons emitted . ( Closed value )
View SolutionRadiation of wavelength 310 nm is incidenton a metal surface of work function 1eV. Find maximum speed of photoelectrons emitted . ( Closed value )
View SolutionWhen light of sufficiently high frequency is incident on a metallic surface, electrons are emitted from the metallic surface. This phenomenon is called photoelectric emission. Kinetic energy of the emitted photoelectrons depends on the wavelength of incident light and is independent of the intensity of light. Number of emitted photoelectrons depends on intensity. (hv−ϕ) is the maximum kinetic energy of emitted photoelectron (where ϕ is the work function of metallic surface). Reverse effect of photo emission produces X-ray. X-ray is not deflected by electric and magnetic fields. Wavelength of a continuous X-ray depends on potential difference across the tuve. Wavelength of charasteristic X-ray depends on the atomic number.
Q. If frequency (υ>υ0) of incident light becomes n times the initial frequency (v), then KE of the emitted photoelectrons becomes (v0 threshold frequency).
View SolutionThe kinetic energy of photoelectrons emitted by a photosensitive surface depends on the internsity of the incident radiation
View SolutionThe peak emission from a black body at a certain temprature occurs at a wavelength of 9000Å. On increase its temperature , the total radiation emmited is increased its 81 times. At the intial temperature when the peak radiation from the black body is incident on a metal surface , it does not cause any photoemission from the surface . After the increase of temperature, the peak from the black body caused photoemission. To bring these photoelectrons to rest , a potential equivalent to the excitation energy between n=2andn=3 bohr levels of hydrogen atoms is required. Find the work function of the metal.
View SolutionStatement-1: The photoelectrons produced by a monochromatic light beam incident on a metal surface have a spread in their kinetic energies.
Statement-2: The work function of the metal varies as a function of depth form the surface.
View Solution
