Radius (rn) of electron in nth orbit versus atomic number (Z) graph is
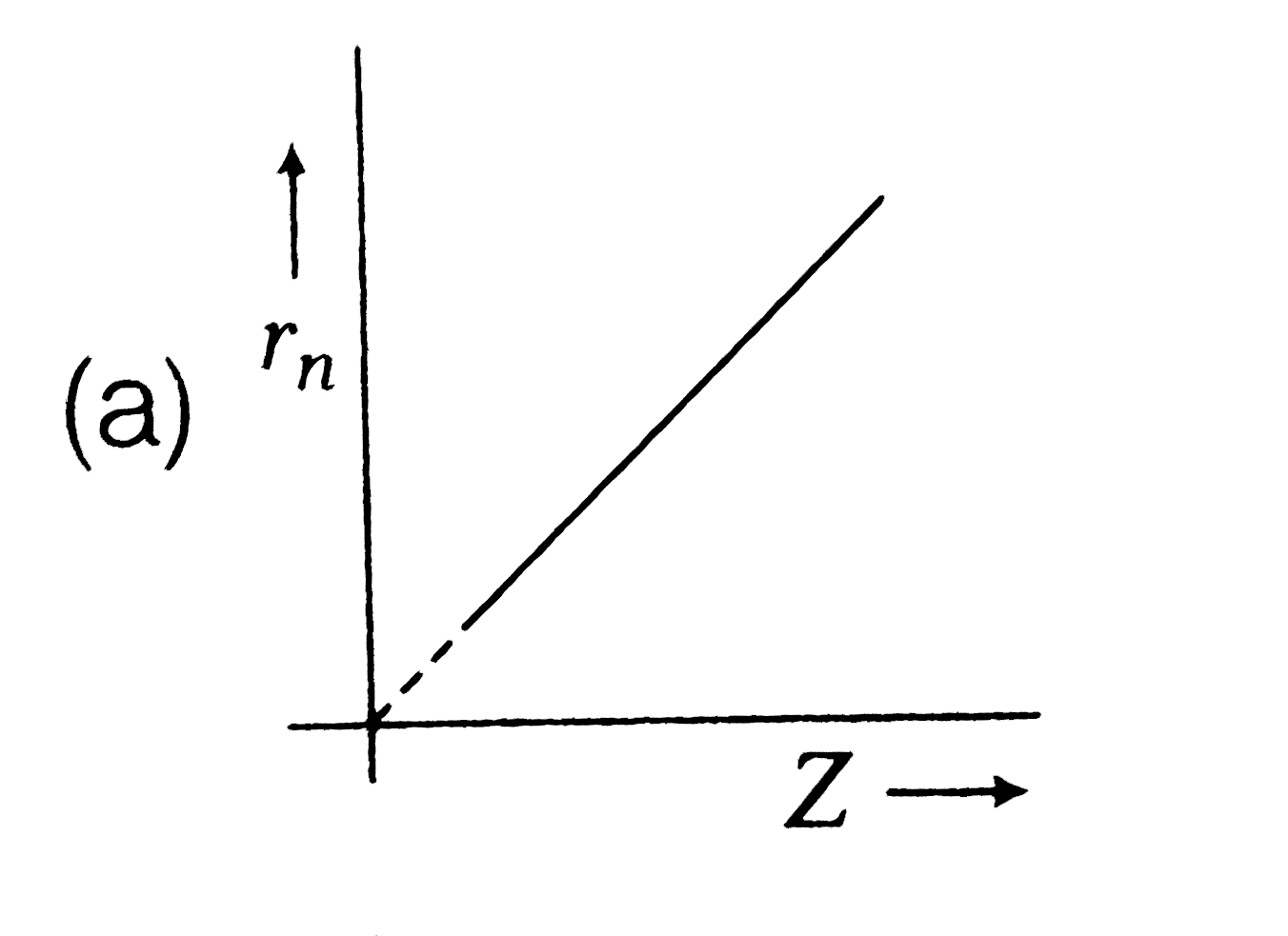
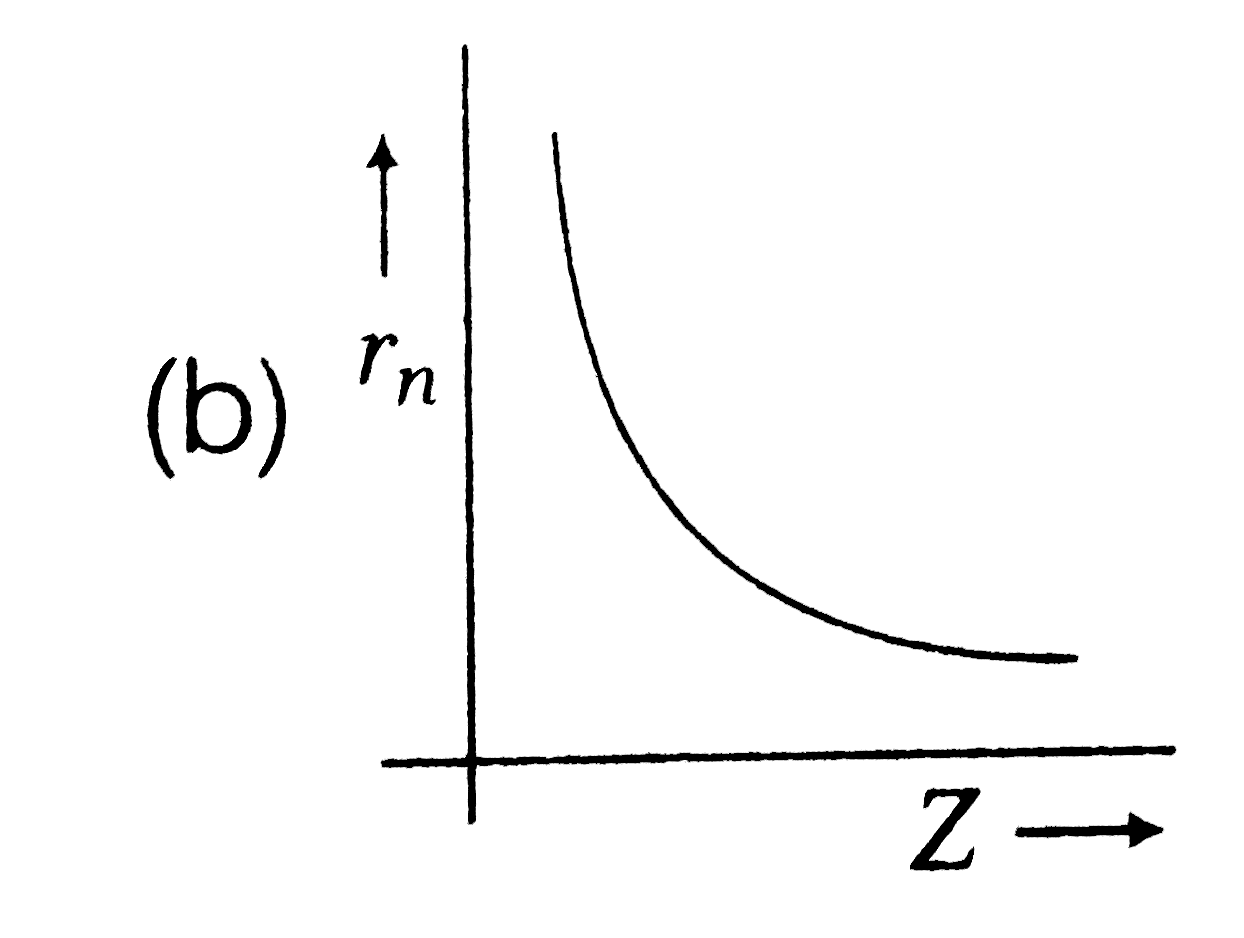
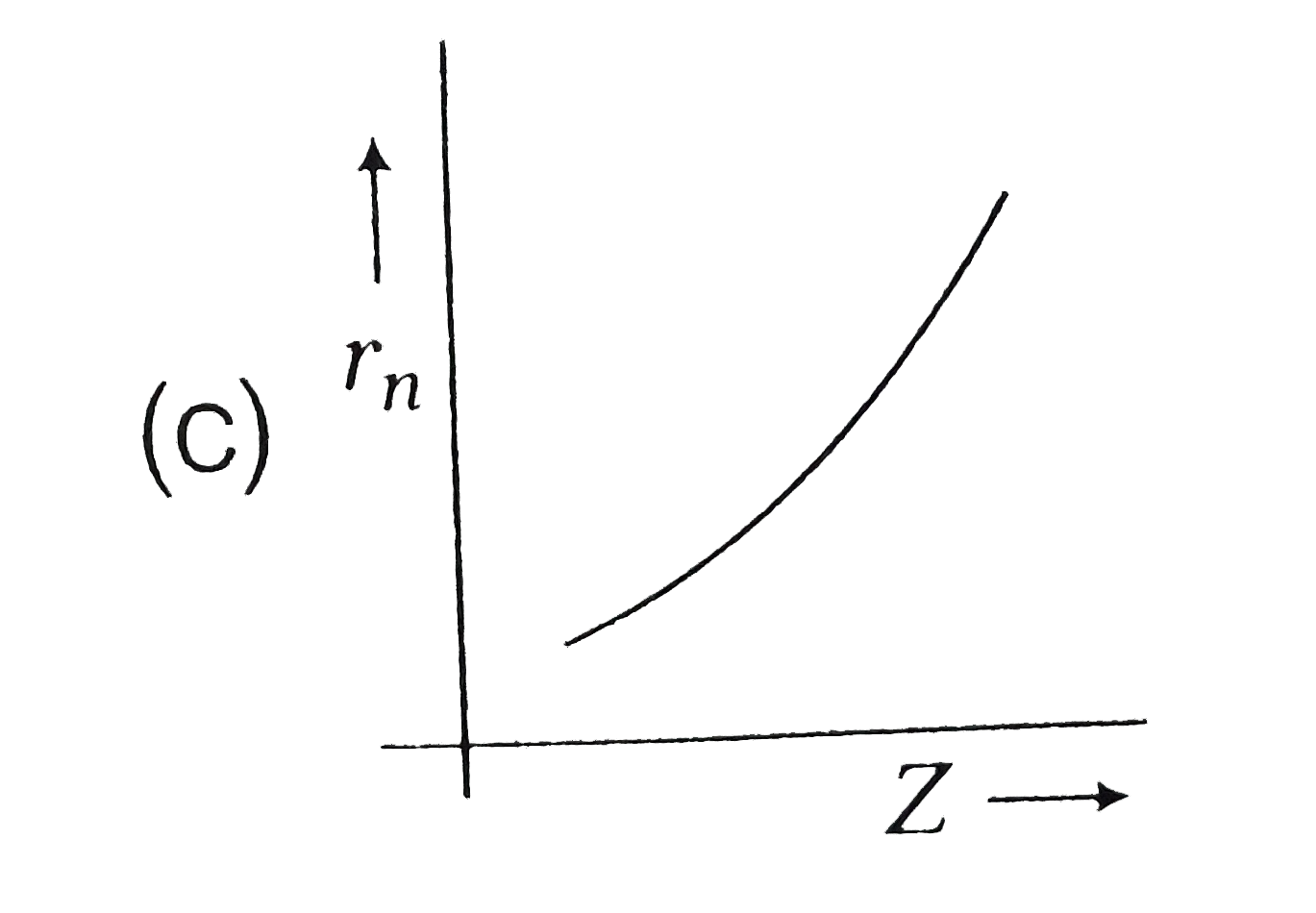
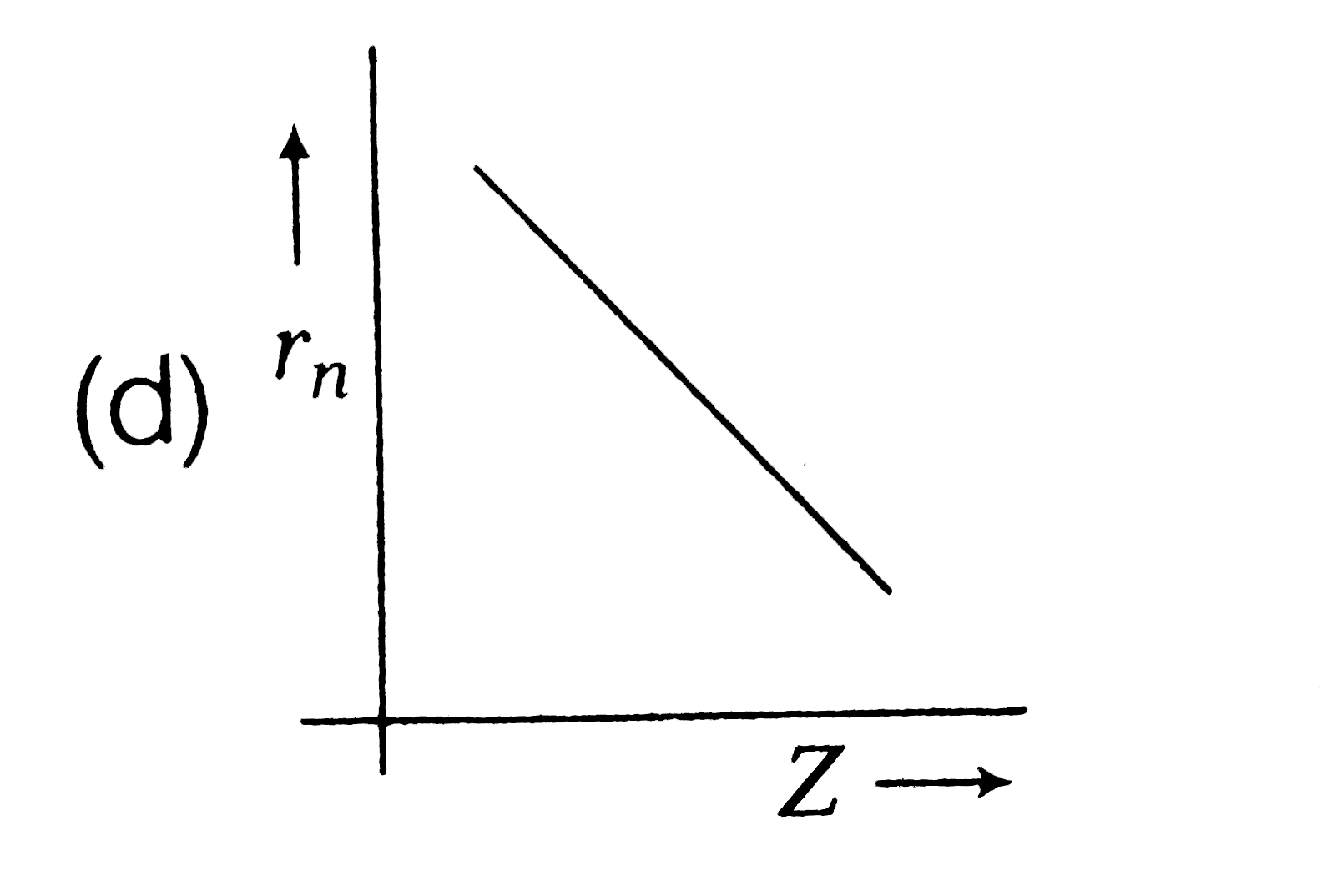
The correct Answer is:B
To analyze the relationship between the radius rn of an electron in the nth orbit and the atomic number Z, we can follow these steps:
1. Understand the Formula:
The radius rn of an electron in the nth orbit is given by the formula:
rn=r0n2Z
where r0 is a constant, n is the principal quantum number (orbit number), and Z is the atomic number.
2. Identify the Relationship:
From the formula, we can see that rn is inversely proportional to Z. This means that as Z increases, rn decreases, and vice versa.
3. Behavior at Extremes:
- When Z=0:
If we substitute Z=0 into the formula, we find that:
rn=r0n20→∞
This indicates that the radius becomes infinitely large when there are no protons (atomic number 0).
- When Z increases:
As Z increases, rn decreases, approaching zero but never actually reaching it.
4. Graph Characteristics:
- The graph of rn versus Z will start from infinity when Z=0 and will decrease as Z increases.
- The curve will approach the horizontal axis (but will never touch it), indicating that rn decreases towards zero as Z becomes very large.
5. Conclusion:
Therefore, the correct graph is one that starts from infinity when Z=0 and decreases towards zero as Z increases.
The radius rn of an electron in the nth orbit is given by the formula:
rn=r0n2Z
where r0 is a constant, n is the principal quantum number (orbit number), and Z is the atomic number.
From the formula, we can see that rn is inversely proportional to Z. This means that as Z increases, rn decreases, and vice versa.
- When Z=0:
If we substitute Z=0 into the formula, we find that:
rn=r0n20→∞
This indicates that the radius becomes infinitely large when there are no protons (atomic number 0).
- When Z increases:
As Z increases, rn decreases, approaching zero but never actually reaching it.
- The graph of rn versus Z will start from infinity when Z=0 and will decrease as Z increases.
- The curve will approach the horizontal axis (but will never touch it), indicating that rn decreases towards zero as Z becomes very large.
Therefore, the correct graph is one that starts from infinity when Z=0 and decreases towards zero as Z increases.
Topper's Solved these Questions
- ATOMSBook:DC PANDEYChapter:ATOMSExercise:Check point 12.2
Explore 16 Videos
- ATOMSBook:DC PANDEYChapter:ATOMSExercise:Check point 12.3
Explore 15 Videos
- ATOMSBook:DC PANDEYChapter:ATOMSExercise:MEDICAL ENTRANCES GALLERY
Explore 42 Videos
- ALTERNATING CURRENTBook:DC PANDEYChapter:ALTERNATING CURRENTExercise:JEE MAIN
Explore 63 Videos
- CAPACITORSBook:DC PANDEYChapter:CAPACITORSExercise:OBJECTIVE_TYPE
Explore 1 Video
Similar Questions
Energy Of Electron In Nth Orbit
View SolutionIn Bohr's model, rn,z= radius of nth orbit with atomic number Z
un,z=P.E of electron in nth orbit with atomic number Z
Kn,z=K.E of electron in nth orbit with atomic number Z
Vn,z= velocity of electron in nth orbit with atomic number Z
Tn,z= time period of revolution in nth orbit with atomic number Z
(ColumnI,ColumnII),((A)U1.2,K1.1,(p)1:8),((B)r2.1,r1.2,(q)−8:1),((C)V1.3,V3.1,(r)9:1),((D)T1.2,T2.2,(s)8:1)
View Solution
Knowledge Check
Speed (Vn) of electron in nth orbit versus principal quantum number (n) graphs is
A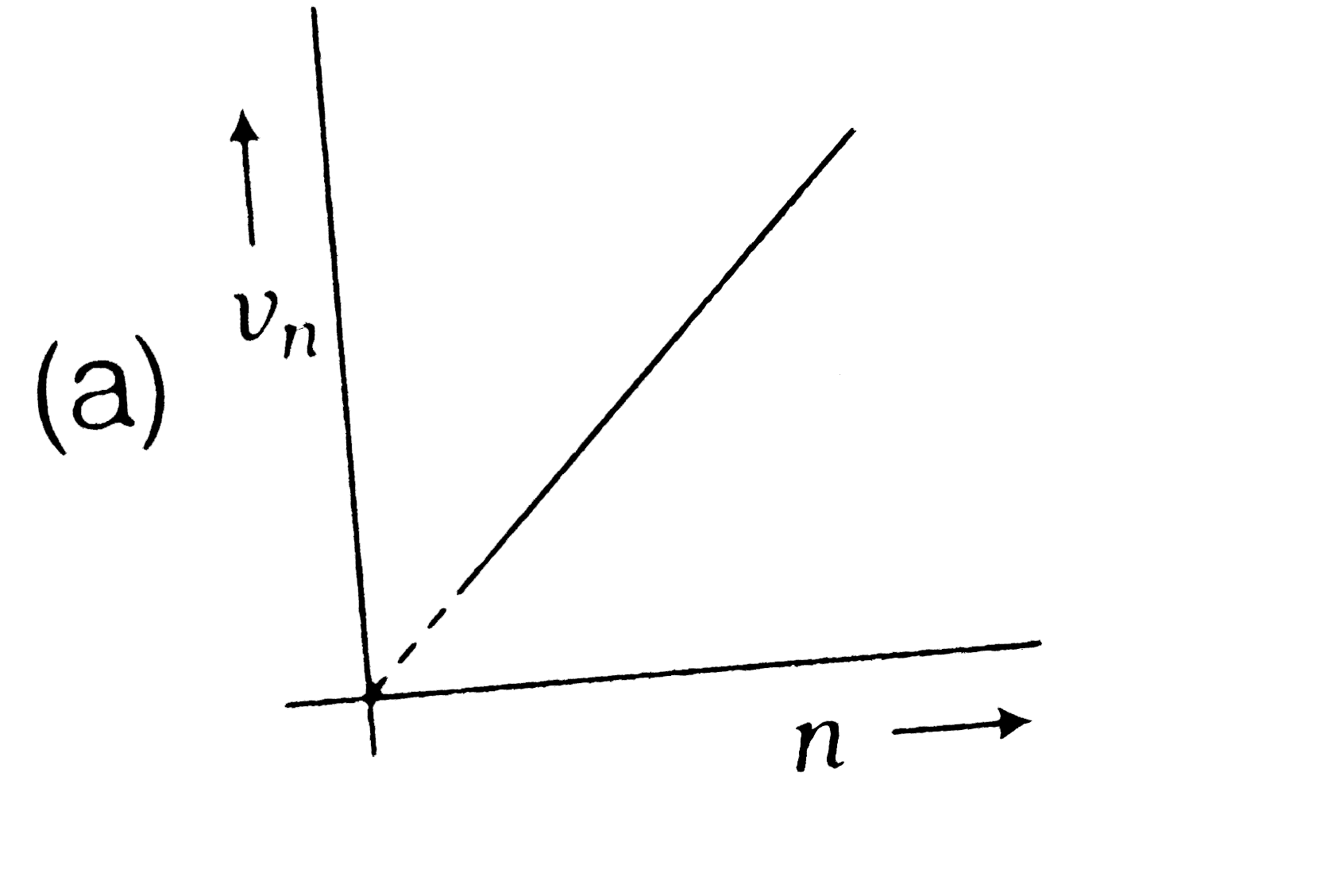 B
B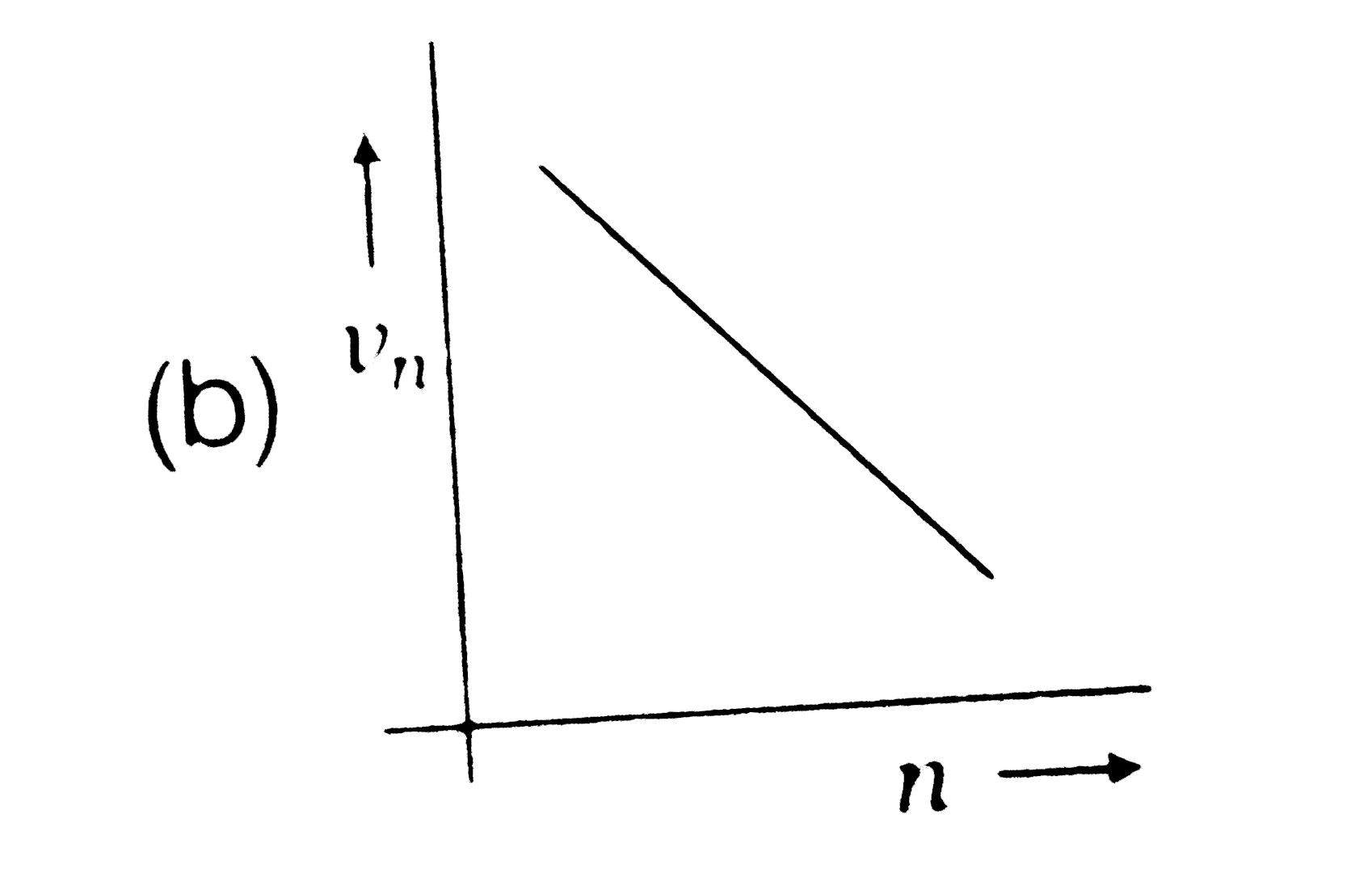 C
C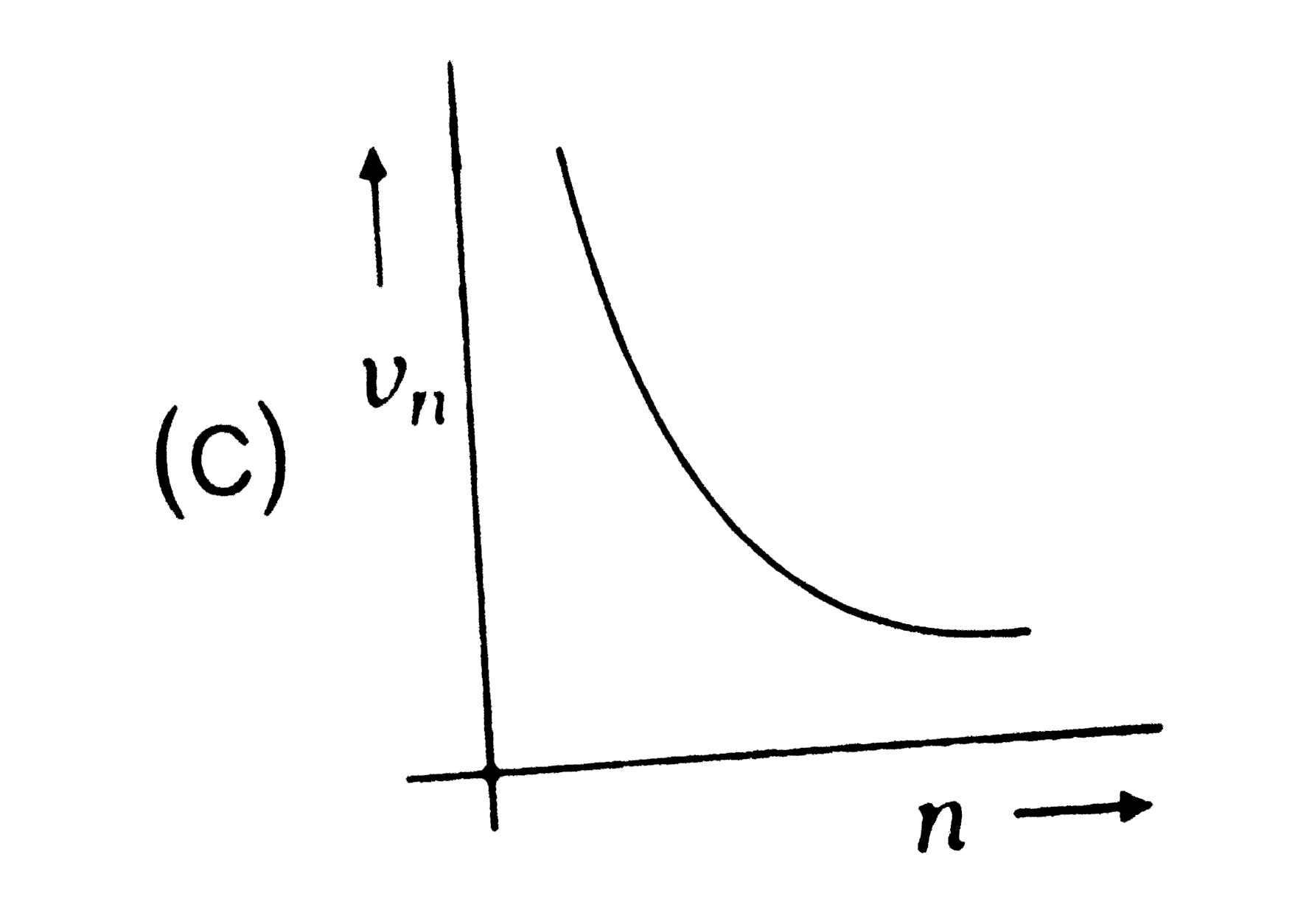 D
D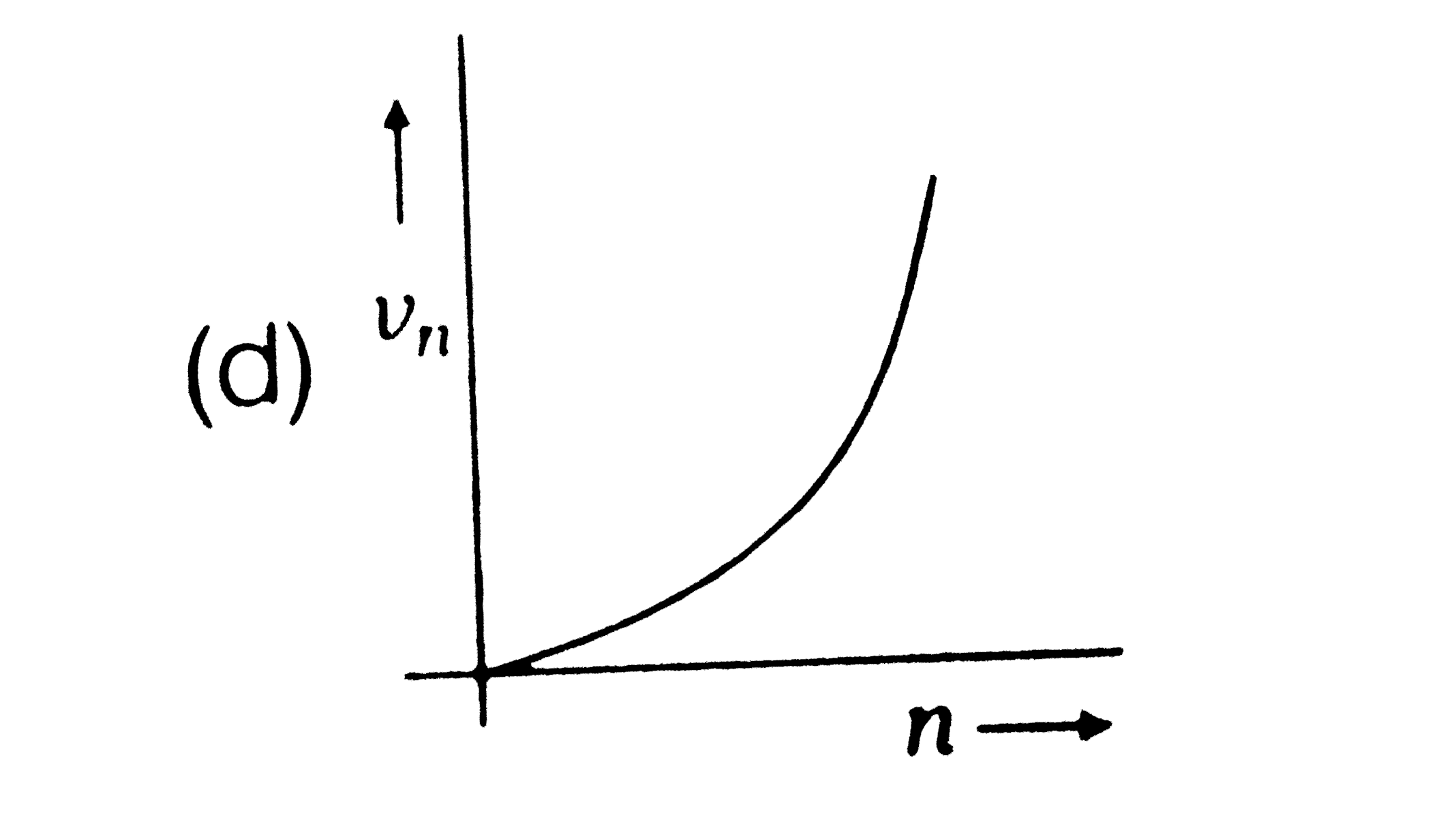
In the Bohr’s model, for unielectronic species following symbols are used,
rn,z→ Radius of nth orbit with atomic number "z".
Un,z→ Potential energy of electron in nth orbit with atomic number "z".
Kn,z→ Kinetic energy of electron innth orbit with atomic number "z".
vn,z→Velocity of electron innth orbit with atomic number "z".
Tn,z→ Time period of revolution of electron in nth orbit with atomic number "z".
Calculate z in all in cases.
(i) U1,2:K1,z=−8:1
(ii) r1,z:r2,1=1:8
(iii) v1,z:v3,1=9:1
(iv) T1,2:T2,z=9:32
Represent your answer as abcd, where a,b,c and d represent number from 0 to 9. a,b,c and d represents the value of "z" in parts (i), (ii), (iii) & (iv). Suppose your answer is 1,2,3 & 4 then the same must be filled in OMR sheet as 1234.00.A2233B1233C3233D4233According to Bohr's theory the radius of electron in an orbit described by principle quantum number n and atomic number Z is proportional to
AZ2n2BZ2n2CZ2nDn2Z
In the Bhor's models for the unielectronic species followingf symbols are used.
rn,z→ Radius of nth orbit with atomic number "Z"
Un,z→Potential energy of electron in nth orbit with atomic number "Z"
Kn,z→Kinetic energy of electron in nth orbit with atomic number "Z"
vn,z→Velocity of electron in nth orbit with atomic number "Z"
Tn,z→Time period of revlution of electron energy of electron in nth orbit with atomic number "Z"
Calulate z in all in cases.
Represent your answer as abcd, where a,b,c and d repersent number from 0 to 9. a,b,c and d
represents the value of "z" in parts (i),(ii),(iii) & (iv) . Suppose your answer is 1,2,3&4 then the same
must be filled in OMR sheet as 12314.00.
View SolutionIn the Bohr's model , for unielectronic species following symbols are used
rn,z→ Radius of nth orbit with atomic number "z"
Un,z→ Potential energy of electron in nth orbit with atomic number "z"
Kn,z→ Kinetic energy of electron in nth orbit with atomic number "z"
Vn,z→ Velocity of electon in nth orbit with atomic number "z"
Tn,z→ Time period of revolution of electon in nth orbit with atomic number "z"
Calculate z in all in cases.
(i)U1,2:K1,z=−8:9
(ii)r1,z:r2,1=1:12
(iii)v1,z:v3,1=15:1
(iv)T1,2:T2,z=9:32
Report your answer as (2r-p-q-s) where p,q,r and s represents the value of "z" in parts (i),(ii),(iii),(iv).
View SolutionVelocity Of Electron In Nth Orbit
View SolutionAccording to Bohr's theory, the radius of an electron in an orbit described by principal quantum number n and atomic number Z is proportional to
View SolutionMagnetic moment of an electron in nth orbit of hydrogen atom is
View Solution