Read the following passage and then answer questions (a) to (d) on the basis of your under- standing of the passage and the related studied concepts.
We are familiar with Ampere.s circuital law which states that for an open surface with a boundary around a current the line integral of magnetic field around the entire boundary of an open surface is equal to μ0 times the total current passing through the surface i.e.
∮→B.→dl=μ0I
Later on, Maxwell showed that for logical consistency, a changing electric field must also produce a magnetic field. In this context Maxwell introduced the concept of a displacement current given as per relation
ID=∈0dϕEdt
Thus, as per generalisation made by Maxwell, the source of a magnetic field is not just the conduction electric current due to following charges but also the time rate of change of electric field. In this way, Maxwell modified Ampere.s circuital law and in its modified the law is expressed as:
∮→B.→dl=μ0[IC+ID]=μ0[IC+∈0dϕEdt]
In all respects, the displacement current has the same physical effects as the conduction current. It is observed that in same cases, e.g., steady electric field in a wire, displacement current may be zero. In other cases, e.g., a capacitor being charged, both conduction and displacement currents may be present in different regions of space. In most of the cases, conduction current and displacement current may be present simultaneously in the same region of space because there exist no perfectly conducting or perfectly insulating medium. Moreover, there may be large regions of space where there is no conduction current but there is only a displacement current due to time varying electric field.
In how many ways a magnetic field produced in free space without the presence of permanent magnet?
(c ) Magnetic field in space may be produced in space under following two conditions :
(i) When current flows through a conductor, magnetic field is set up around it.
(ii) When electric field in a given region is varying with time, it also produces a magnetic field in the region.
Topper's Solved these Questions
- BOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - MULTIPLE CHOICE QUESTIONS25videos
ELECTROMAGNETIC WAVES
- BOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - FILL IN THE BLANKS14videos
ELECTROMAGNETIC WAVES
- BOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ADDITIONAL EXERCISES10videos
ELECTROMAGNETIC WAVES
- BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SELF ASSESSMENT TEST (SECTION-B) (VERY SHORT ANSWER QUESTIONS)4videos
ELECTRIC CHARGES AND FIELDS
- BOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D1videos
ELECTROMAGNETICE INDUCTION
Similar Questions
Which of the following radiation has the least wavelength?
02:44View SolutionIf μ0 be the magnetic permeability are ε0 the electric permittivity of free space then speed of em waves in freee space is given as : c = ______________.
View SolutionSuppose that the electric field part of an electromagnetic wave in vacuum is →E={(3.1N/C)cos[(1.8rad/m)y+(5.4×106rad/s)t]}ˆi.
(a) What is the direction of propagation?
(b) What is the wavelength λ?
(c ) What is the frequency v?
(d) What is the amplitude of the magnetic field part of the wave?
(e) Write an expression for the magnetic field part of the wave.View SolutionThree small , identical point charges lie on the circumference of a circle forming an equilateral triangle.Calculate the value of electric field at the centre of circle.
02:17View Solution(a) Derive the expression for the magnetic energy stored in an inductor when a current I develops in it. Hence, obtain the expression for the magnetic energy density.
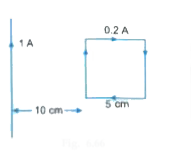
(b) A square loop of sides 5 cm carrying a current of 0.2 A in the clockwise direction is placed at a distance of 10 cm from an infinitely long wire carrying a current of 1 A as shown in Fig. 6.66. Calculate (i) the resultant magnetic force, and (ii) the torque, if any, acting on the loop.
 01:45View Solution
01:45View SolutionDraw the magnetic field lines around a straight conductor carrying current. Name and state the rule to find the direction of magnetic field.
View SolutionOn flowing current in a conducting wire the magnetic field produces around it.‛ It is a law of
View SolutionA charge particle of charge 'q' and mass 'm' enters in a given magnetic field 'B' and perpendicular to the magnetic field as shown in the figure. It enters at an angle of 60^(@) with the boundary surface of magnetic field and comes out at an angle of 30^(@) with the boundary surface of the magnetic field as shown in the figure. Find width 'd' in which magnetic field exist.
06:18View Solution"On passing current in a conducting wire, the magnetic field is produced around it." It is a law of
View SolutionGive the direction of current passing through an open surface.
View SolutionMagnetic field lines around a current carrying straight conductor are concentric circles.
View SolutionState the rule of determine the direction of magnetic field around a current - carrying wire .
02:57View SolutionWhat is solenoid ? Draw the field lines of the magnetic field produced on passing current through and around a current carrying solenoid.
01:53View SolutionRead the following passage and then answer questions (a) to (d) on the basis of your under- standing of the passage and the related studied concepts.
We are familiar with Ampere.s circuital law which states that for an open surface with a boundary around a current the line integral of magnetic field around the entire boundary of an open surface is equal to μ0 times the total current passing through the surface i.e.
∮→B.→dl=μ0I
Later on, Maxwell showed that for logical consistency, a changing electric field must also produce a magnetic field. In this context Maxwell introduced the concept of a displacement current given as per relation
ID=∈0dϕEdt
Thus, as per generalisation made by Maxwell, the source of a magnetic field is not just the conduction electric current due to following charges but also the time rate of change of electric field. In this way, Maxwell modified Ampere.s circuital law and in its modified the law is expressed as:
∮→B.→dl=μ0[IC+ID]=μ0[IC+∈0dϕEdt]
In all respects, the displacement current has the same physical effects as the conduction current. It is observed that in same cases, e.g., steady electric field in a wire, displacement current may be zero. In other cases, e.g., a capacitor being charged, both conduction and displacement currents may be present in different regions of space. In most of the cases, conduction current and displacement current may be present simultaneously in the same region of space because there exist no perfectly conducting or perfectly insulating medium. Moreover, there may be large regions of space where there is no conduction current but there is only a displacement current due to time varying electric field.
Define displacement current.View SolutionRead the following passage and then answer questions (a) to (d) on the basis of your under- standing of the passage and the related studied concepts.
We are familiar with Ampere.s circuital law which states that for an open surface with a boundary around a current the line integral of magnetic field around the entire boundary of an open surface is equal to μ0 times the total current passing through the surface i.e.
∮→B.→dl=μ0I
Later on, Maxwell showed that for logical consistency, a changing electric field must also produce a magnetic field. In this context Maxwell introduced the concept of a displacement current given as per relation
ID=∈0dϕEdt
Thus, as per generalisation made by Maxwell, the source of a magnetic field is not just the conduction electric current due to following charges but also the time rate of change of electric field. In this way, Maxwell modified Ampere.s circuital law and in its modified the law is expressed as:
∮→B.→dl=μ0[IC+ID]=μ0[IC+∈0dϕEdt]
In all respects, the displacement current has the same physical effects as the conduction current. It is observed that in same cases, e.g., steady electric field in a wire, displacement current may be zero. In other cases, e.g., a capacitor being charged, both conduction and displacement currents may be present in different regions of space. In most of the cases, conduction current and displacement current may be present simultaneously in the same region of space because there exist no perfectly conducting or perfectly insulating medium. Moreover, there may be large regions of space where there is no conduction current but there is only a displacement current due to time varying electric field.
What did Maxwell suggest to make Ampere.s circuital law logical consistent?04:14View Solution

