Relativistic corrections become necessary when the expression for the kinetic energy 12mv2, becomes comparable with mc2, where m is the mass of the particle. At what de-broglie wavelength will relativistic corrections become important for an electron?
λ=10nm
λ=10−1nm
λ=10−4nm
λ=10−6nm
To determine at what de Broglie wavelength relativistic corrections become important for an electron, we start by comparing the kinetic energy expression 12mv2 with the rest energy mc2. Relativistic effects become significant when the kinetic energy is comparable to the rest energy.
1. Understand the de Broglie Wavelength:
The de Broglie wavelength λ of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
2. Relate Momentum to Velocity:
The momentum p can be expressed as:
p=mv
Thus, we can rewrite the de Broglie wavelength as:
λ=hmv
3. Express Velocity in Terms of Wavelength:
Rearranging the equation gives us:
v=hmλ
4. Kinetic Energy Expression:
The kinetic energy K of the electron is given by:
K=12mv2
Substituting v from the previous step:
K=12m(hmλ)2=h22mλ2
5. Set Kinetic Energy Equal to Rest Energy:
For relativistic corrections to be necessary, we set the kinetic energy equal to the rest energy:
h22mλ2≈mc2
6. Solve for Wavelength:
Rearranging the equation to find λ:
λ2≈h22m2c2
Taking the square root:
λ≈h√2mc
7. Substituting Values:
- Planck's constant h=6.626×10−34Js
- Mass of the electron m=9.11×10−31kg
- Speed of light c=3×108m/s
Plugging in these values:
λ≈6.626×10−34√2×9.11×10−31×3×108
8. Calculating the Value:
- Calculate the denominator:
√2×9.11×10−31×3×108≈3.87×10−22
- Now calculate λ:
λ≈6.626×10−343.87×10−22≈1.71×10−12m=1.71pm
Conclusion:
Relativistic corrections become important for an electron when its de Broglie wavelength is approximately 1.71pm.
---
The de Broglie wavelength λ of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
The momentum p can be expressed as:
p=mv
Thus, we can rewrite the de Broglie wavelength as:
λ=hmv
Rearranging the equation gives us:
v=hmλ
The kinetic energy K of the electron is given by:
K=12mv2
Substituting v from the previous step:
K=12m(hmλ)2=h22mλ2
For relativistic corrections to be necessary, we set the kinetic energy equal to the rest energy:
h22mλ2≈mc2
Rearranging the equation to find λ:
λ2≈h22m2c2
Taking the square root:
λ≈h√2mc
- Planck's constant h=6.626×10−34Js
- Mass of the electron m=9.11×10−31kg
- Speed of light c=3×108m/s
λ≈6.626×10−34√2×9.11×10−31×3×108
- Calculate the denominator:
√2×9.11×10−31×3×108≈3.87×10−22
- Now calculate λ:
λ≈6.626×10−343.87×10−22≈1.71×10−12m=1.71pm
Relativistic corrections become important for an electron when its de Broglie wavelength is approximately 1.71pm.
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTERBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- CURRENT ELECTRICITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Very Short Answer Type Question.
20 Videos
- ELECTRIC CHARGES AND FIELDBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDEXERCISE - Long Answer Type Question
6 Videos
Similar Questions
A 2 mg sand particle is blown with a speed of 50m/sec what is the its de Broglie's wavelength ?
View SolutionTwo particles of masses m and 2m have equal kinetic energies. Their de Broglie wavelengths area in the ratio of:
View SolutionIf E1,E2andE3 represent respectively the kinetic energies of an electron, an α−partic≤ and a proton each having same de-Broglie wavelength, then
View SolutionAt temperature T , the average kinetic energy of any particles is 32 kT. The de Broglie wavelength follows the order :
View SolutionFind the ratio of kinetic energy of the particle to the energy of the photon . If the de Broglie wavelength of a particle moving with a velocity 2.25×108m/s is equal to the wavelength of photon .
View Solutionde Broglie wavelengths of two particles A and B are plotted against (1√V) , where V is the potential on the particles. Which of the following relation is correct about the mass of the particles ?
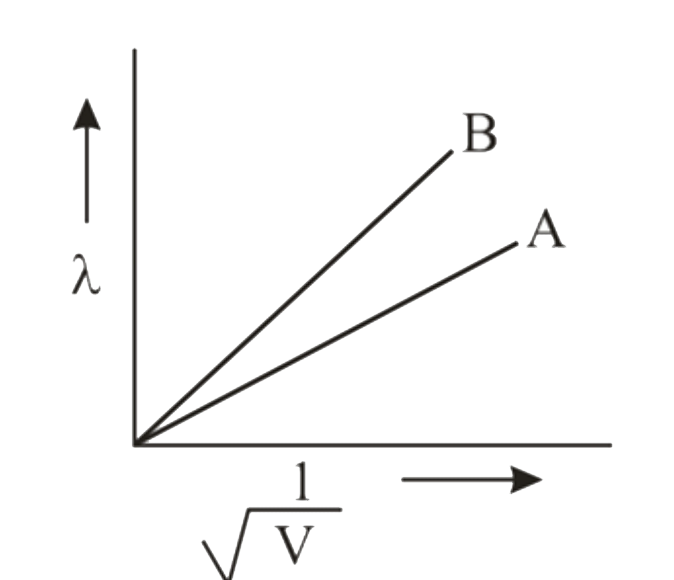
View SolutionFor two particles A and B, curves are plotted √V against de-Broglie wavelengths, where V is the potential on the particles. Which of the following relation is correct about the mass of particles?
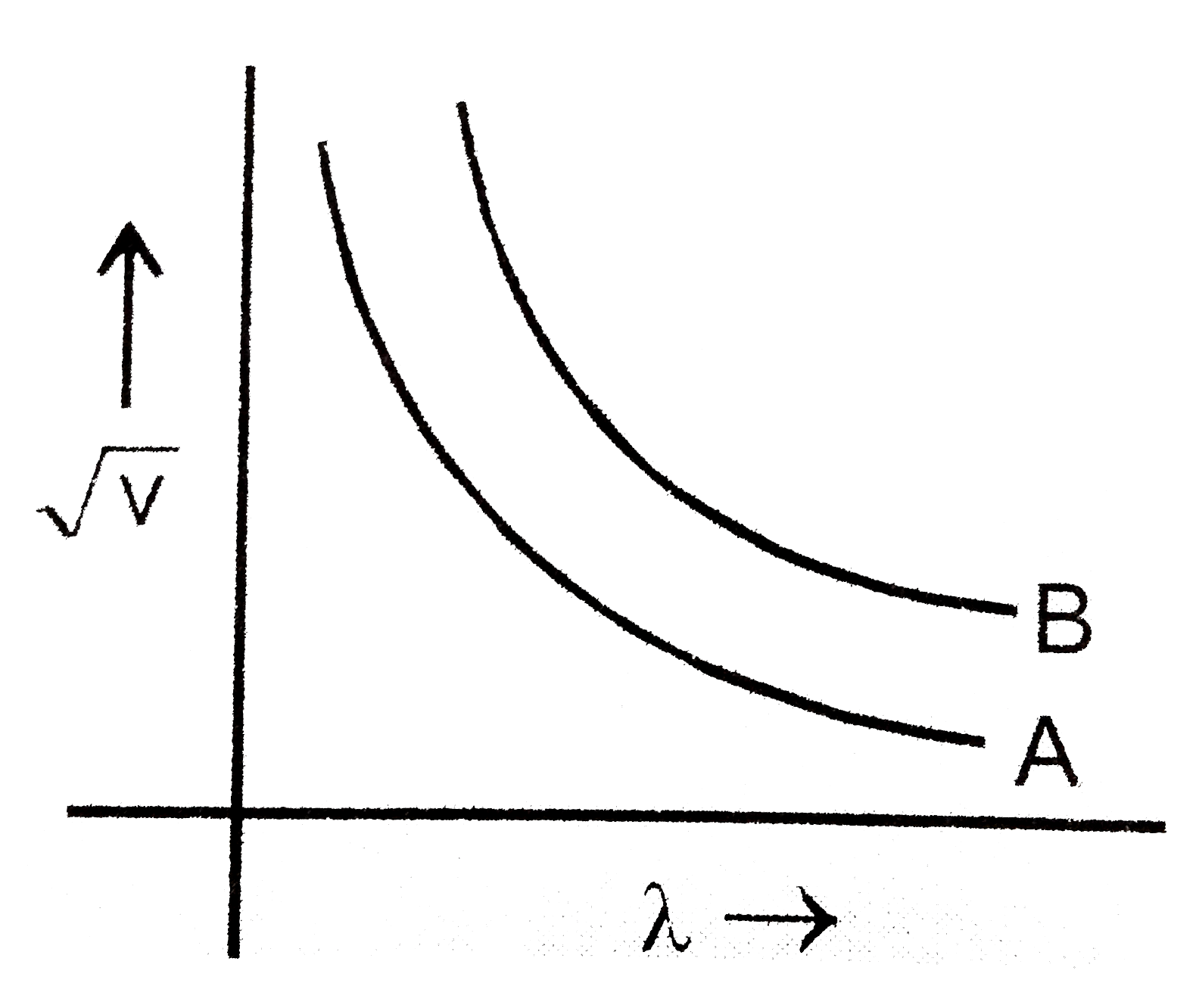
View SolutionDe-Broglie wavelengths of the particle increases by 75% then kinetic energy of particle becomes.
View SolutionAn electron with initial kinetic energy of 100eV is acclerated through a potential difference of 50V. Now the de-Brogile wavelength of electron becomes
View SolutionTwo particles A1andA2 of masses m1,m2(m1>m2) have the same de-broglie wavelength. Then
View Solution
