Relativistic corrections become necessary when the expression for the kinetic energy 12mv2, becomes comparable with mc2, where m is the mass of the particle. At what de-broglie wavelength will relativistic corrections become important for an electron?
λ=1nm
λ=10nm
λ=10−1
λ=10−4
The correct Answer is:D
To determine at what de Broglie wavelength relativistic corrections become important for an electron, we follow these steps:
Step 1: Understand the condition for relativistic corrections
Relativistic corrections become necessary when the kinetic energy K of the particle becomes comparable to its rest energy mc2. The kinetic energy of a particle is given by:
K=12mv2
where m is the mass of the particle and v is its velocity. The rest energy is given by:
E0=mc2
Step 2: Set the condition for relativistic corrections
We set the kinetic energy equal to the rest energy:
12mv2≈mc2
This simplifies to:
v2≈2c2
Taking the square root gives:
v≈√2c
Step 3: Relate velocity to de Broglie wavelength
The de Broglie wavelength λ is given by:
λ=hp
where p is the momentum of the particle. The momentum p can also be expressed as:
p=mv
Thus, we can rewrite the de Broglie wavelength as:
λ=hmv
Step 4: Substitute the velocity condition into the de Broglie wavelength
Substituting v≈√2c into the de Broglie wavelength equation gives:
λ≈hm√2c
Step 5: Insert known values for Planck's constant and the mass of the electron
Using the values:
- h=6.626×10−34J s
- m=9.1×10−31kg
- c=3×108m/s
We can calculate:
λ≈6.626×10−349.1×10−31⋅√2⋅3×108
Step 6: Calculate the numerical value
Calculating the denominator:
m√2c≈9.1×10−31⋅1.414⋅3×108≈3.85×10−22
Now substituting this back into the wavelength equation:
λ≈6.626×10−343.85×10−22≈1.72×10−12m or 1.72pm
Step 7: Conclusion
Relativistic corrections become important for an electron when the de Broglie wavelength is approximately 1.72pm.
Relativistic corrections become necessary when the kinetic energy K of the particle becomes comparable to its rest energy mc2. The kinetic energy of a particle is given by:
K=12mv2
where m is the mass of the particle and v is its velocity. The rest energy is given by:
E0=mc2
We set the kinetic energy equal to the rest energy:
12mv2≈mc2
This simplifies to:
v2≈2c2
Taking the square root gives:
v≈√2c
The de Broglie wavelength λ is given by:
λ=hp
where p is the momentum of the particle. The momentum p can also be expressed as:
p=mv
Thus, we can rewrite the de Broglie wavelength as:
λ=hmv
Substituting v≈√2c into the de Broglie wavelength equation gives:
λ≈hm√2c
Using the values:
- h=6.626×10−34J s
- m=9.1×10−31kg
- c=3×108m/s
λ≈6.626×10−349.1×10−31⋅√2⋅3×108
Calculating the denominator:
m√2c≈9.1×10−31⋅1.414⋅3×108≈3.85×10−22
Now substituting this back into the wavelength equation:
λ≈6.626×10−343.85×10−22≈1.72×10−12m or 1.72pm
Relativistic corrections become important for an electron when the de Broglie wavelength is approximately 1.72pm.
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - DAVISSON AND GERMER EXPERIMENT
3 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - HIGHER ORDER THINKING SKILLS
8 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - PARTICLE NATURE OF LIGHT : THE PHOTON
19 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Assertion And Reason
15 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A 2 mg sand particle is blown with a speed of 50m/sec what is the its de Broglie's wavelength ?
View SolutionTwo particles of masses m and 2m have equal kinetic energies. Their de Broglie wavelengths area in the ratio of:
View SolutionIf E1,E2andE3 represent respectively the kinetic energies of an electron, an α−partic≤ and a proton each having same de-Broglie wavelength, then
View SolutionAt temperature T , the average kinetic energy of any particles is 32 kT. The de Broglie wavelength follows the order :
View SolutionFind the ratio of kinetic energy of the particle to the energy of the photon . If the de Broglie wavelength of a particle moving with a velocity 2.25×108m/s is equal to the wavelength of photon .
View Solutionde Broglie wavelengths of two particles A and B are plotted against (1√V) , where V is the potential on the particles. Which of the following relation is correct about the mass of the particles ?
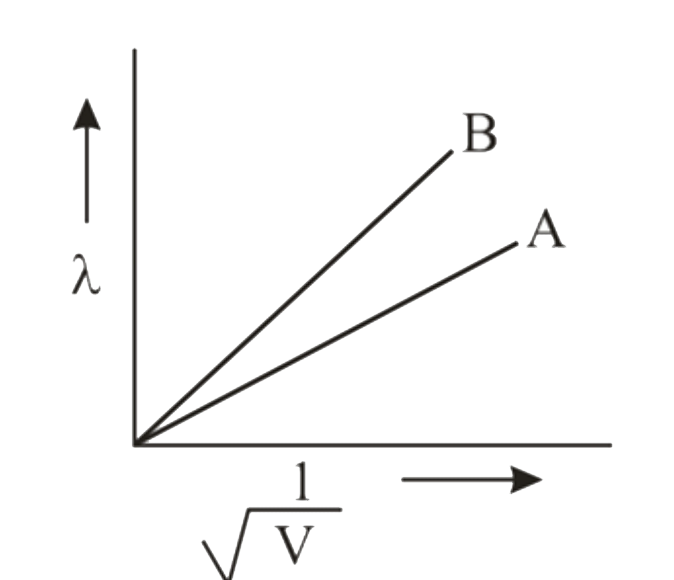
View SolutionFor two particles A and B, curves are plotted √V against de-Broglie wavelengths, where V is the potential on the particles. Which of the following relation is correct about the mass of particles?
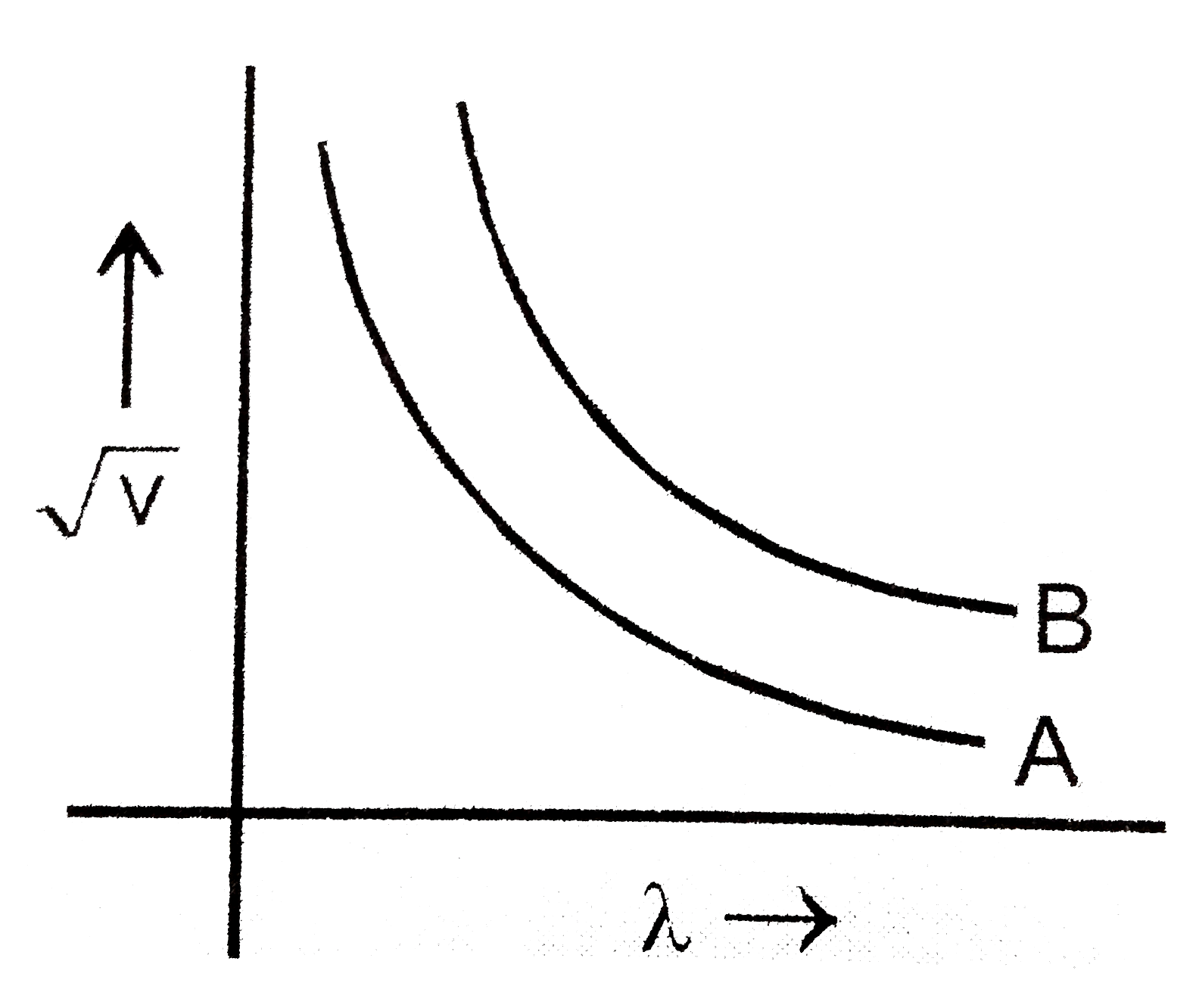
View SolutionDe-Broglie wavelengths of the particle increases by 75% then kinetic energy of particle becomes.
View SolutionAn electron with initial kinetic energy of 100eV is acclerated through a potential difference of 50V. Now the de-Brogile wavelength of electron becomes
View SolutionTwo particles A1andA2 of masses m1,m2(m1>m2) have the same de-broglie wavelength. Then
View Solution
