Sand is piled up on a horizontal ground in the form of a regular cone of a fixed base radius R. The coefficient of static friction between sand layers is μ . The maximum volume of sand that can be pilled up, without the sand slipping on the surface is
μR33π
μR33
πR33μ
μπR33
The correct Answer is:D
To solve the problem of finding the maximum volume of sand that can be piled up in the form of a regular cone without slipping, we can follow these steps:
Step 1: Understand the Geometry of the Cone
We have a cone with:
- Base radius R
- Height h
- Slant height l
The relationship between the height h, radius R, and the slant height l is given by the right triangle formed by these dimensions. The angle θ is defined as the angle between the height and the slant height.
Step 2: Relate Height and Radius Using the Angle
Using the definition of tangent in the context of the cone:
tan(θ)=hR
This means that:
h=Rtan(θ)
Step 3: Apply the Condition for Static Friction
For the sand not to slip, the condition is:
tan(θ)<μ
Substituting the expression for h:
hR<μ
This implies:
h<μR
Step 4: Determine the Maximum Height
The maximum height hmax of the sand cone can be expressed as:
hmax=μR
Step 5: Calculate the Volume of the Cone
The volume V of a cone is given by the formula:
V=13πR2h
Substituting hmax into the volume formula:
Vmax=13πR2hmax=13πR2(μR)
This simplifies to:
Vmax=13πμR3
Final Answer
Thus, the maximum volume of sand that can be piled up without slipping is:
Vmax=πμR33
---
We have a cone with:
- Base radius R
- Height h
- Slant height l
Using the definition of tangent in the context of the cone:
tan(θ)=hR
This means that:
h=Rtan(θ)
For the sand not to slip, the condition is:
tan(θ)<μ
Substituting the expression for h:
hR<μ
This implies:
h<μR
The maximum height hmax of the sand cone can be expressed as:
hmax=μR
The volume V of a cone is given by the formula:
V=13πR2h
Substituting hmax into the volume formula:
Vmax=13πR2hmax=13πR2(μR)
This simplifies to:
Vmax=13πμR3
Thus, the maximum volume of sand that can be piled up without slipping is:
Vmax=πμR33
Similar Questions
A car is taking turn on a circular path of radius R. If the coefficient of friction between the tyres and road is μ, the maximum velocity for no slipping is
View SolutionA car has to move on a level turn of radius 45 m. If the coefficient of static friction between the tyre and the road is μs=2.0, find the maximum speed the car can take without skidding.
View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to

View SolutionA block is kept on a horizontal table. The table is undergoing simple farmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friction between the block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface g=10ms−1
View SolutionA horizontal force F acts on the sphere at its centre as shown. Coefficient of friction between ground and sphere is μ. What is maximum value of F for which there is no slipping?
View SolutionA horizontal force F acts on the sphere at its centre as shown. Coefficient of friction between ground and sphere is μ. What is maximum value of F for which there is no slipping?
View SolutionA solid sphere of mass 3kg is kept on a horizontal surface. The coefficient of static friction between the surfaces in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface? (in N)
View SolutionTwo hemispheres of radii R and r(<R) are fixed on a horizontal table touching each other (see figure). A uniform rod rests on to spheres as shown. The coefficient of friction between the rod and two spherers is μ. Then the maximum value of the ratio rR for which the rod will not slide is :

View SolutionThere block A B ,and C of equal mass m are placed one over the other on a frictionless surface (table) as shown in figure The coefficient of friction between any blocks A ,B and C is μ The maximum value of mass of block D so that the blocks A,B and C move without slipping over each other is
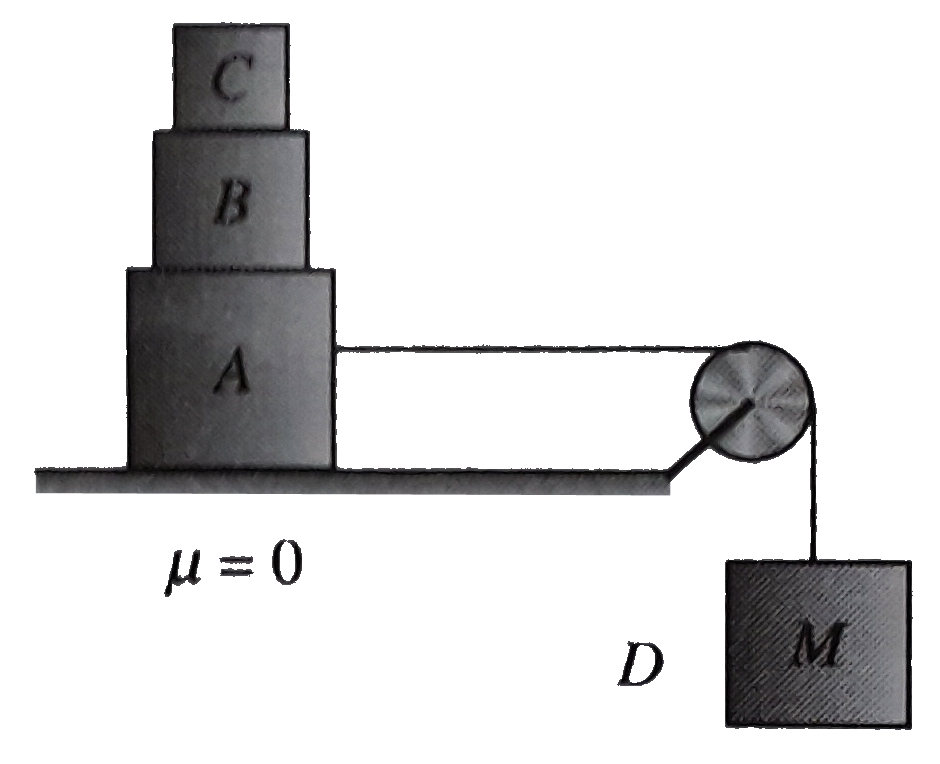
View SolutionA solid sphere of mass 0.50 kg is kept on a horizontal surface. The coefficient of static friction between the surfaces in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface?
View Solution
