Shape of a string transmitting wave along x-axis some instant is shown. Velocity of point P v - (4π)cm /s (θ) = tan−1(0.004pi) 
Amplitube of wave is 2 mm
Velocity of wave is 10 m/s
Maximum acceleration of particle is 80π2cm/sec2
Wave is travelling in negative x-direction
The correct Answer is:A, B, C, D
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Comprehion Type Questions
19 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Matrix Matching
16 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - ONLY ONE OPTION IS CORRECT
62 Videos
- VECTORSBOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
y−x curve at an instant for a wave travelling along x−axis on a string is shown. Slope at the point A on the curve, as shown, is tan53∘.
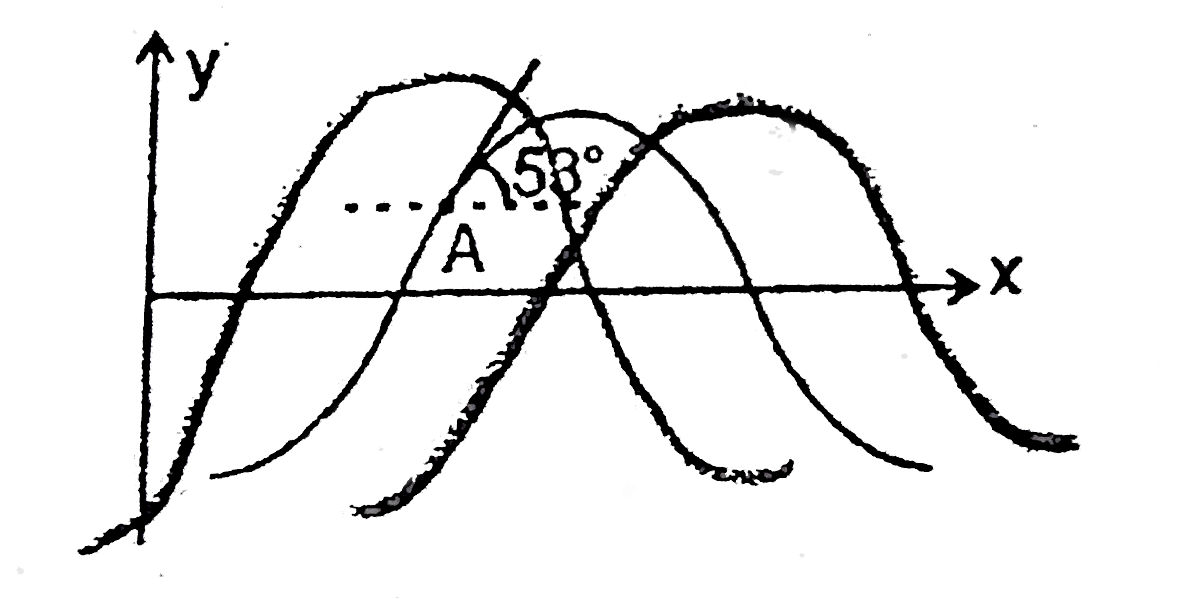
View Solutiony−x curve at an instant for a wave travelling along x−axis on a string is shown. Slope at the point A on the curve, as shown, is tan53∘.
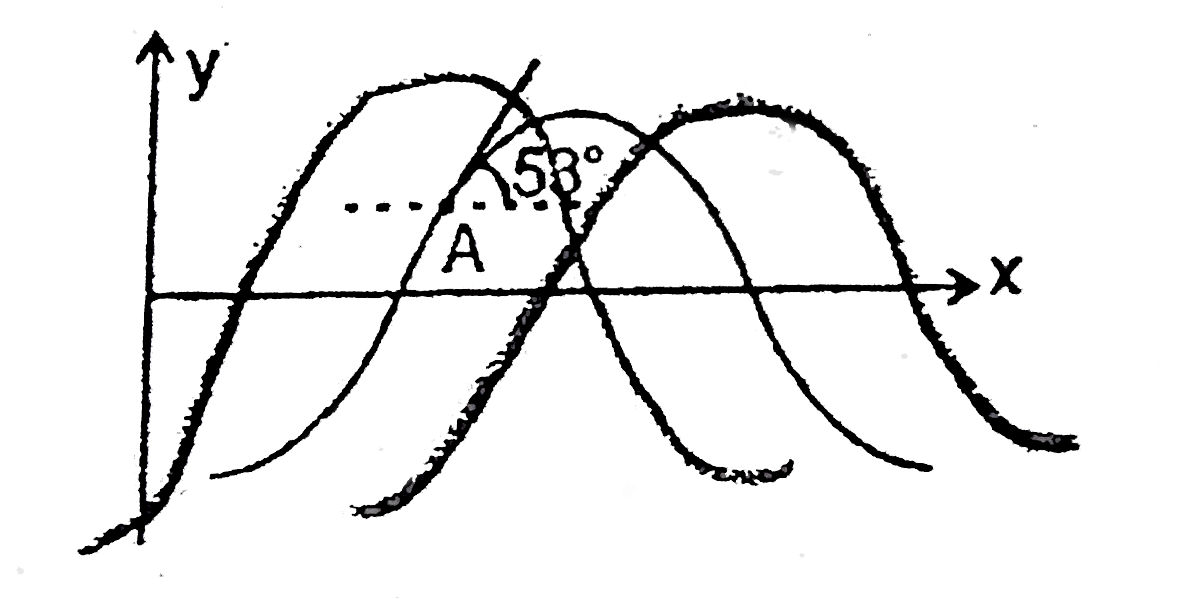
View Solution
Knowledge Check
y−x curve at an instant for a wave travelling along x−axis on a string is shown. Slope at the point A on the curve, as shown, is tan53∘.
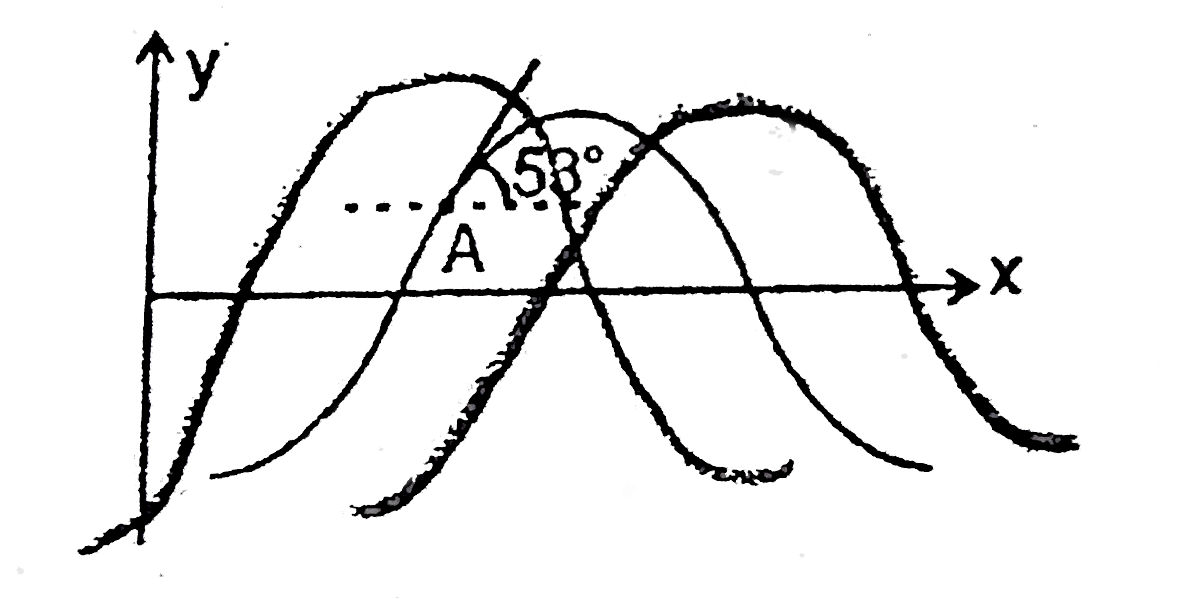 ATransverse velocity of the particle at point A is positive if the wave is travelling along positive x−axis.BTransverse velocity of the particle at point A is positive if the wave is travelling along negative x−axis of the particle at point ACMagnitude of transverse velocity of the particle at point A is greater than wave speed.DMagnitude of transverse velocity of the particle at point A is lesser than wave speed.
ATransverse velocity of the particle at point A is positive if the wave is travelling along positive x−axis.BTransverse velocity of the particle at point A is positive if the wave is travelling along negative x−axis of the particle at point ACMagnitude of transverse velocity of the particle at point A is greater than wave speed.DMagnitude of transverse velocity of the particle at point A is lesser than wave speed.A disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is
 A→VP=(v+vrsinθR)ˆi+vrcosθRˆjB→VP=(v+vrsinθR)ˆi−vrcosθRˆjC→VP=vrsinθRˆi+vrcosθRˆjD→VP=vrsiθRˆi−vrcosθRˆj
A→VP=(v+vrsinθR)ˆi+vrcosθRˆjB→VP=(v+vrsinθR)ˆi−vrcosθRˆjC→VP=vrsinθRˆi+vrcosθRˆjD→VP=vrsiθRˆi−vrcosθRˆjA transverse wave on a string travelling along + ve x-axis has been shown in the figure below:
The mathmetical form of the shown wave is
y=(3.0cm)sin[2π×0.1t−2π100x]
where t is in seconds and x is in centimetres. Find the total distance travelled by the particle at (1) in 10 min 15 s. measured from the instant shown in the figure and direction of its motion at the end of this time.
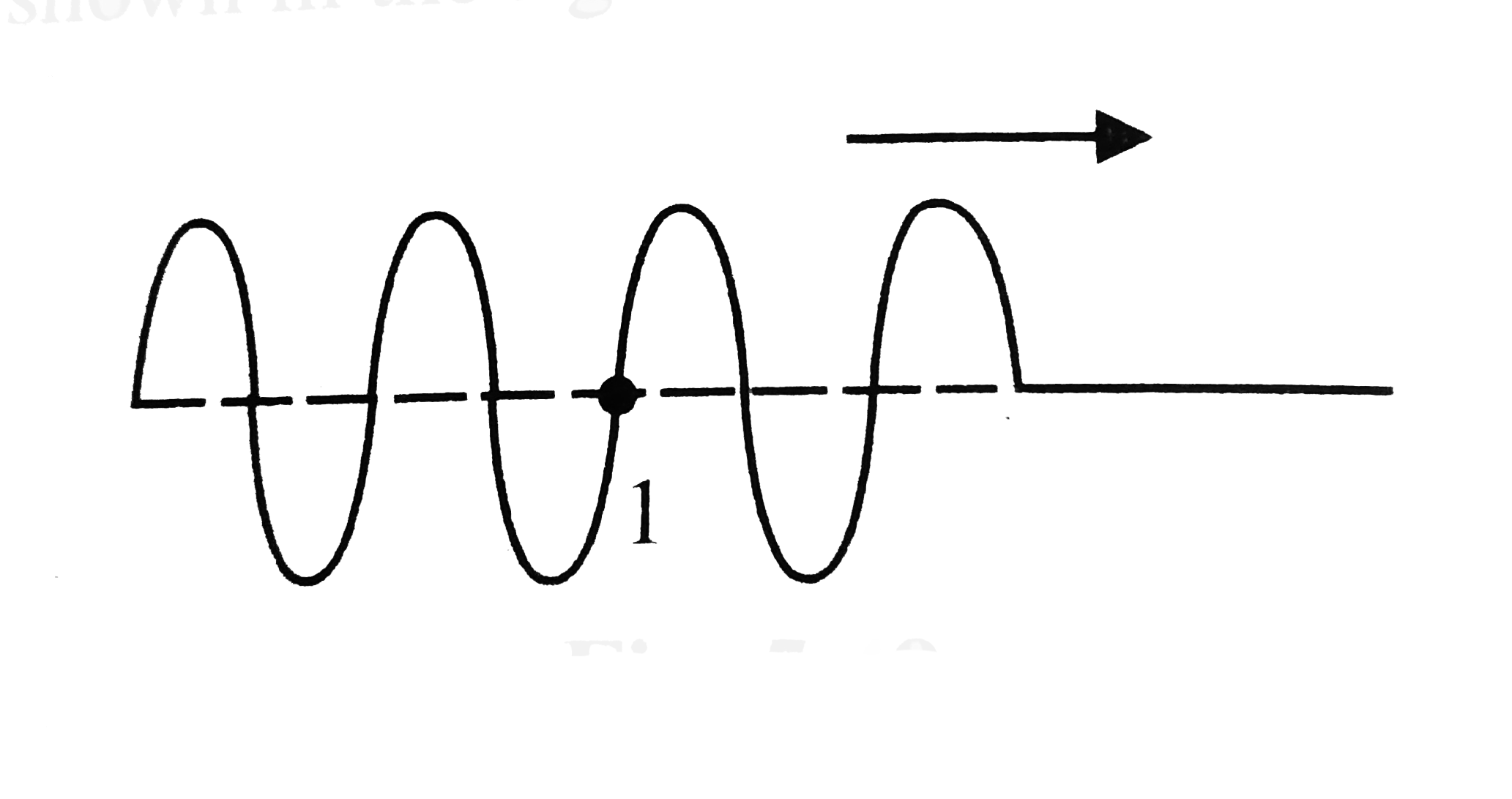 A6 cm, in upward directionB6 cm, in downward directiionC738 cm, in upward directionD732 cm, in upward direction
A6 cm, in upward directionB6 cm, in downward directiionC738 cm, in upward directionD732 cm, in upward direction
A disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is

View SolutionA transverse sinusoidal wave moves along a string in the positive x-direction at a speed of 10cm/s. The wavelength of the wave is 0.5 m and its amplitude is 10cm. At a particular time t,the snapshot of the wave is shown in figure. The velocity of point P when its displacement is 5 cm is

(a) √3π50ˆjm/s
(b)−√3π50ˆjm/s
(c)√3π50ˆim/s
(d) −√3π50ˆim/s
View SolutionA transverse wave on a string travelling along + ve x-axis has been shown in the figure below:
The mathmetical form of the shown wave is
y=(3.0cm)sin[2π×0.1t−2π100x]
where t is in seconds and x is in centimetres. Find the total distance travelled by the particle at (1) in 10 min 15 s. measured from the instant shown in the figure and direction of its motion at the end of this time.

View SolutionSnapshot of a string carrying a progressive wave is shown in figure at time t = 0. The wave moves along positive x - axis:
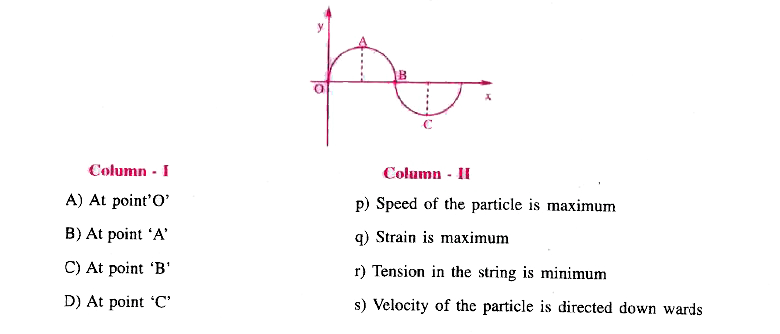
View SolutionThe displacement of a vibrating string versus position along the string is shown in the figure. The periodic wave have a speed of 10.0cm/s. A and B are two points on the string.
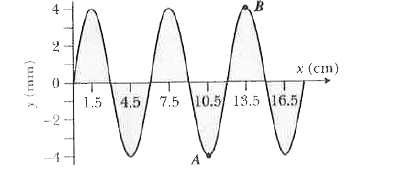
What is the wavelength of the wave?
View Solution
