show a smooth spherical ball of mass m striking two identical equilateral triangular wedges of mass M. At the instant of impact velocity of the ball is υ0. Taking coefficient of restitution e, determine the velcities of the sphere and the wedges just after collision.

Step by step video & image solution for show a smooth spherical ball of mass m striking two identical equilateral triangular wedges of mass M. At the instant of impact velocity of the ball is upsilon_(0). Taking coefficient of restitution e, determine the velcities of the sphere and the wedges just after collision. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - Level 1110videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - L-221videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type13videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN12videos
RIGID BODY MOTION
Similar Questions
A sphere of mass m moving with a uniform velocity v hits another identical sphere at rest. If the coefficient of restitution is e, the ratio of the velocities of the two sphere after the collision is e−1e+1.
View SolutionA glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View Solution
Knowledge Check
- Question 1 - Select One
A sphere of mass m moving with a constant velocity u hits another stationary sphere of the same mass and of coefficient of restitution (e). The ratio of velocities of the two spheres, after collision, will be
Ae(e+1)B(1−e1+e)C1eD(e+1e) - Question 2 - Select One
A ball of mass m moving with a constant velocity strikes against a ball of same mass at rest. If e= coefficient of restitution, then what will the the ratio of the velocities of the two balls after collision?
A1−e1+eBe−1e+1C1+e1−eD2+ee−1 - Question 3 - Select One
The first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
A1−e1+eB1+e1−eC1+e2D1−e2
A body of mass m moving with a velocity strikes a stationary body having same mass . What will be the ratio of velocity of two bodies after the collision if the coefficient of restitution is e .
View SolutionA particle of mass m moving with speed u hits a wedge of mass M as shown in figure. If coefficient of restitution is e and friciton can be neglected, then find the speed of the wedge with respect to ground just after the collision.
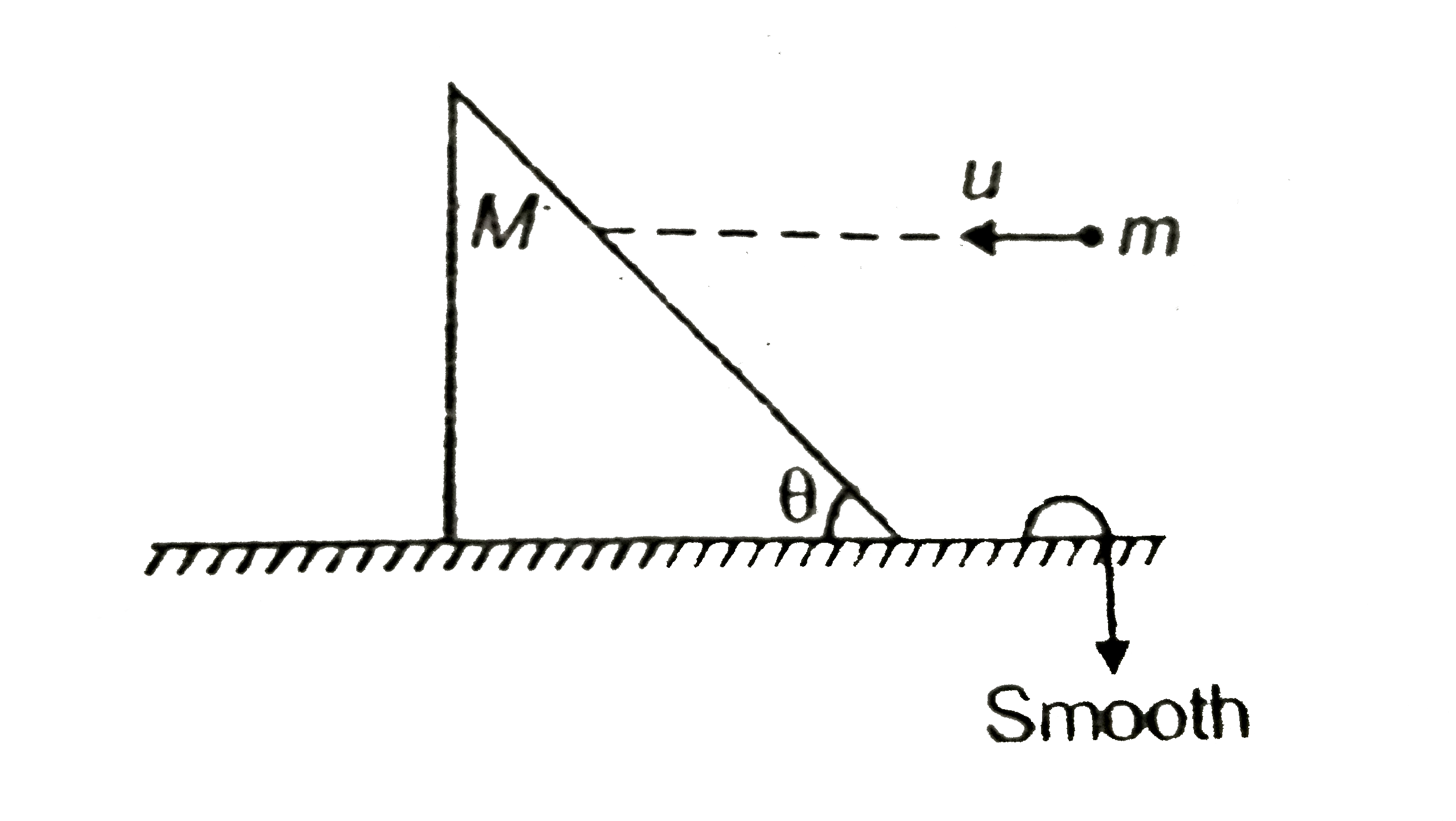 View Solution
View SolutionBall 1 collides with another identical ball at rest. For what value of coefficient of restitution e, the velocity of second ball becomes two times that of 1 after collision? _____.
View SolutionA sphere of mass m moving with a velocity u hits another stationary sphere of same mass. If e is the coefficient of restitution, what is the ratio of the velocities of two spheres after the collision?
View SolutionA glass ball collides with a smooth horizontal surface (xz plane) with a velocity V=ai−bj. If the coefficient of restitution of collision be e, the velocity of the ball just after the collision will be
View Solution

