Show four steps of carnot engine in P-V graph write the equation of each step and obtain the work done by the system. Also obtain the efficiency of a carnot engine.Solution in Gujrati
There are four reversible process occur in carnot engine.
(1) isothermal expansion
(2) Adiabatic expansion
(3) Isothermal compression
(4) Adiabatic compression
A cylic process is obtain by these four processes is shown in below P → V diagram.
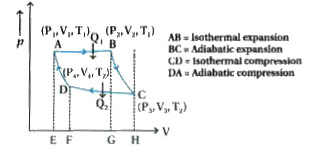
(a) Step 1: Isothermal expansion of gas taking its state from (P1,V1,T1) to (P2,V2,T1). For this, the conducting bottom of the cylinder is brought into contact with the heat and the gas is slowly allowed to expand isothermally.
(b) The heat absorbed by the gas Q1 from the reservoir, hence work done by gas (or on surrounding)
W1=Q1=μRT1ln(V2V1)...(1)
Where μ is amount of gas in mole
R=Gas constant or W1=Q1=Area of ABGEA
(b) Step 2: (Adiabatic expansion) : Now, the cylinder is placed on a thermally insulated stand and gas is adiabatically expanded from state (P2,V2,T1) to (P3,V3,T2) (Here temperature decreases due to expansion). The work done by the gas in adiabatic expansion (or on surrounding)
W2=μR(T1−T2)γ−1...(2)
OR
∴W2= Area of BCHGB
(c) Step 3: (Isothermal compression): Now the cylinder is brought in contact with heat sink and isothermally compressed slowly and brought from (P3,V3,T2) to (P4,V4,T2). During this process heat released Q2 by the gas to the reservoir (sink) at temperature T2. The work done on the gas (or by surrounding)
W3=−Q2=−μRT2ln(V4V3)
∴W3=Q2=μRT2ln(V3V4)...(3)
(Here work done on the system and system rejected heat so W and Q2 are negative)
OR W3=Q2 =Area of CDFHC
(d) Step 4: (Adiabatic compression): Now the cylinder is placed on a thermally insulated stand and the gas is compressed adiabatically and is taken from state to [P4,V4,T2] to [P1,V1,T1]
The work done on the gas (work done by surrounding) in adiabatic compression.
W4=−μR[T2−T1]γ−1
∴W4=μR[T1−T2]γ−1....(4)
OR W4 = Area of ADFEA
Total work done by the gas in one complete cycle from equation (1),(2),(3) and (4) ,
W=W1+W2→(−W3)+(−W4)
But W2=W4
[∵W2 is the work done by gas and W4 is the work done on the gas]
∴W=W1−W3...(5)
[∵W1>0,W3<0]
=Area of ABCDA
Now efficiency of engine,
η=WQ1
=W1−W3Q1=Q1−Q2Q1
=1−Q2Q1
∴η=1−μRT2ln(V3V4)μRT1ln(V2V1)
∴η=1−T2ln(V3V4)T1ln(V2V1) ...(6)
(From equ. (1) and (3))
For adiabatic process TVγ−1 = constant
∴ For step → 2
T1Vγ−12=T2Vγ−13
∴(V2V3)γ−1=T2T1
∴V2V3=(T2T1)1γ−1 ...(7)
and for step → 4
V1V4=(T2T1)1γ−1 ....(8)
From equation (7) and (8) ,
V2V3=V1V4
∴V2V1=V3V4....(9)
From equation (6) and (9) ,
η=1−T2T1 is the efficiency of carnot engine
Topper's Solved these Questions
- THERMODYANMICS BOOK - KUMAR PRAKASHANCHAPTER - THERMODYANMICS EXERCISE - Section-A (Try Your self )
90 Videos
- THERMODYANMICS BOOK - KUMAR PRAKASHANCHAPTER - THERMODYANMICS EXERCISE - Section-B Numericals (Numerical From Textual Exercise)
10 Videos
- THERMAL PROPERTIES OF MATTERBOOK - KUMAR PRAKASHANCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks
1 Videos
- UNITS AND MEASUREMENTBOOK - KUMAR PRAKASHANCHAPTER - UNITS AND MEASUREMENTEXERCISE - Section -F (Questions from Module )
20 Videos
Similar Questions
Which form of heat believed in before the modern time ?
View SolutionA geyser heats water flowing at the rate of 3.0 litres per minute from 27∘ C to 77∘C. If the geyser operates on a gas burner, what is the rate of consumption of the fuel if its heat of combustion is 4.0×104 J/g ?
View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
View SolutionIf the error in measurement of radius of a shpere is 2% then the error in determination of volume of the sphere will be …………
View SolutionA Carnot engine works between 600K and 300K. The efficiency of the engine is
View SolutionThe efficiency of a Carnot heat engine
View SolutionEfficiency of Carnot engine is 100% if
View SolutionA Carnot heat engine has an efficiency of 10% . If the same engine is worked backward to obtain a refrigerator, then find its coefficient of performance.
View SolutionThe efficiency of carnot engine depends on
View SolutionObtain the formula for the coefficient of performance of carnot engine.
View SolutionBy which one of the following working temperature the efficiency of a carnot engine obtained maximum ?
View SolutionThe efficiency of a carnot engine η=110. This carnot engine used as refrigerator. If work done on system is 10 J, then heat absorbed from sink will be …….
View SolutionWrite the expression for the efficiency of a Carnot engine.
View SolutionEfficiency of a carnot engine is_____of the nature of working substance.
View SolutionA Carnot engine works between 600K and 300K. The efficiency of the engine is
View Solution
