Show that the angular momentum about any point of a single particle moving with constant velocity remains constant throughout the motion. Is there any external torque on the particle ?
To show that the angular momentum of a single particle moving with constant velocity remains constant throughout the motion, we can follow these steps:
Step 1: Define Angular Momentum
Angular momentum (L) of a particle about a point is defined as:
L=r×p
where r is the position vector from the point to the particle, and p is the linear momentum of the particle.
Step 2: Express Linear Momentum
The linear momentum p of the particle can be expressed as:
p=mv
where m is the mass of the particle and v is its velocity.
Step 3: Analyze the Motion
Since the particle is moving with constant velocity, both m and v are constants. Therefore, the linear momentum p remains constant throughout the motion.
Step 4: Consider the Position Vector
Let r be the position vector of the particle relative to a chosen point (the origin). As the particle moves, the position vector r changes, but the direction of motion (velocity vector) remains constant.
Step 5: Calculate Angular Momentum
The magnitude of the angular momentum can be calculated as:
|L|=|r||p|sinθ
where θ is the angle between r and p.
Step 6: Identify the Perpendicular Distance
The term rsinθ represents the perpendicular distance from the line of motion (along which the particle is moving) to the point about which we are calculating the angular momentum. This distance remains constant as the particle moves along its path.
Step 7: Conclude Angular Momentum is Constant
Since both |p| (momentum) and rsinθ (perpendicular distance) are constant, the angular momentum L remains constant throughout the motion:
L=mv⋅(rsinθ)=constant
Step 8: Check for External Torque
To determine if there is any external torque acting on the particle, we can use the relationship:
τ=dLdt
If the angular momentum is constant (dLdt=0), then the torque τ must also be zero. Thus, there is no external torque acting on the particle.
Conclusion
We have shown that the angular momentum of a single particle moving with constant velocity about any point remains constant throughout the motion, and there is no external torque acting on the particle.
---
Angular momentum (L) of a particle about a point is defined as:
L=r×p
where r is the position vector from the point to the particle, and p is the linear momentum of the particle.
The linear momentum p of the particle can be expressed as:
p=mv
where m is the mass of the particle and v is its velocity.
Since the particle is moving with constant velocity, both m and v are constants. Therefore, the linear momentum p remains constant throughout the motion.
Let r be the position vector of the particle relative to a chosen point (the origin). As the particle moves, the position vector r changes, but the direction of motion (velocity vector) remains constant.
The magnitude of the angular momentum can be calculated as:
|L|=|r||p|sinθ
where θ is the angle between r and p.
The term rsinθ represents the perpendicular distance from the line of motion (along which the particle is moving) to the point about which we are calculating the angular momentum. This distance remains constant as the particle moves along its path.
Since both |p| (momentum) and rsinθ (perpendicular distance) are constant, the angular momentum L remains constant throughout the motion:
L=mv⋅(rsinθ)=constant
To determine if there is any external torque acting on the particle, we can use the relationship:
τ=dLdt
If the angular momentum is constant (dLdt=0), then the torque τ must also be zero. Thus, there is no external torque acting on the particle.
We have shown that the angular momentum of a single particle moving with constant velocity about any point remains constant throughout the motion, and there is no external torque acting on the particle.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE353videos
System of particles & rotational Motion
- BOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice90videos
ROTATIONAL MOTION
- BOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise449videos
Thermal Properties of Matter
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle moves with constant angular velocity in a circle. During the motion its
AEnergy is conservedBMomentum is conservedCEnergy and momentum both are conservedDNone of the above is conserved - Question 2 - Select One
The angular momentum of a moving body remains constant if
Anet external force is appliedBnet external torque is appliedCnet pressure is appliedDnet external torque is not applied . - Question 3 - Select One
Angular momentum of the particle rotating with a central force is constant due to
Aconstant forceBConstant linear momentumCConstant torqueDZero torque.
Which of the following graphs represents the motion of a particle moving with constant velocity?
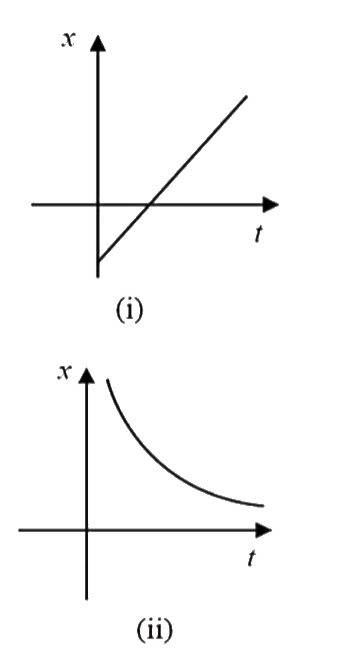
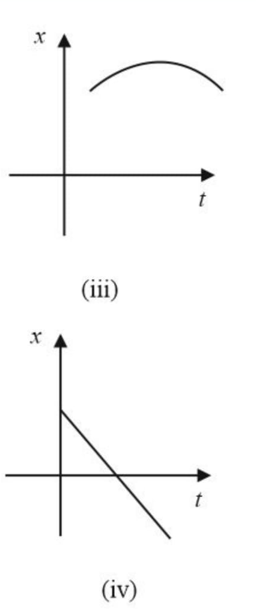 View Solution
View SolutionShow that the angular momentum of a particle is equal to twice the product of mass and areal velocity.
View SolutionShow that the angular momentum of a particle is equal to twice the product of mass and areal velocity.
View SolutionAngular momentum of the particle rotating with a central force is constant due to
View SolutionAngular momentum of the particle rotating with a central force is constant due to.
View Solution

