Show that the coefficient of area expansions $(Δ A / A) / Δ T$ of a rectangular sheet of the solid is twice its linear expansivity $α$ .

Video Solution

Text Solution

Verified by Experts

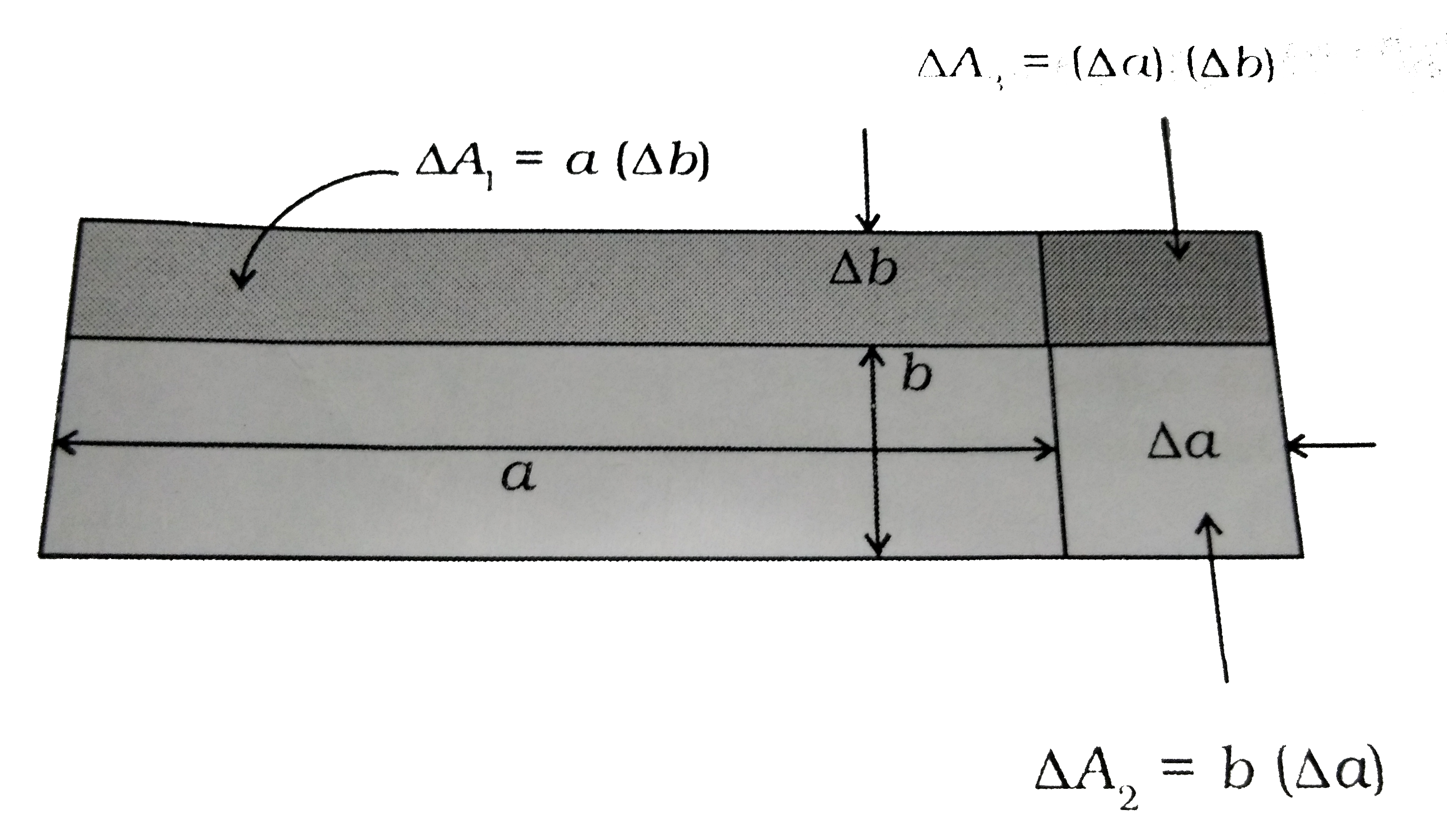Consider a rectangular sheet of the solid material of length a and breadth b.When the temperature increases by $Δ T$ , a increases by $Δ a = (α_{l}) a Δ T$ and b increases by $Δ b = (α_{l}) b Δ T$ ,the increase in area
$Δ A = Δ A_{1} + Δ A_{2} + Δ A_{3}$
$Δ A = a Δ b + b Δ a + (Δ a) (Δ b)$
$Δ A = a (α_{l}) b Δ T + b (α_{l}) a Δ T + {(α_{l})}_{l}^{2} a b {(Δ T)}^{2}$
$Δ A = α_{l} a b Δ T (2 + α_{l} Δ T) = α_{l} A Δ T (2 + α_{l} Δ T)$

Since $α_{l} = 10^{- 5} K^{- 1}$ , the product $α_{l} Δ T$ for fractional temperature is small in comparision with 2 and may be neglected.
Hence,
$(\frac{Δ A}{A}) \frac{1}{Δ T} = 2 α_{l}$

|

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The unit of coefficient of linear expansion is
A $.^{\circ} C$
B $m^{\circ} C^{- 1}$
C $.^{\circ} C^{- 1}$
D $m^{\circ} C$
The unit of the coefficient of linear expansion is
Am
B $/^{\circ - -} C$
C $m /^{\circ - -} C$
D $^{\circ - -} C$
The coefficient of linear expansion of a solid depends upon
Athe unit of pressure
Bthe nature of the material only
Cthe nature of the material and temperature
Dunit of mass

NCERT-THERMAL PROPERTIES OF MATTER-EXERCISE

Home
Ask Doubt
Profile