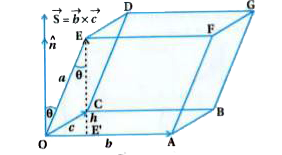
Show that →a.(→b×→c) is equal in magnitude to the volume of the parallelopiped formed on the three vectors, →a,→band→c
 Solution in Gujrati
Solution in Gujrati
Suppose −−→OA=→b,−−→OC=→cand−−→OE=→a →band→c are adjacent sides of parallelogram OABC
Area of □OABC,→S=→b×→c
∴Sˆn=→b×→c
where ˆn unit vector perpendicular to plane form by →band→candθ is angle between →aand→S.
∴→a.(→b×→c)=→a.→S[∵→b×→c=→S]
=aScosθ
=(acosθ)S
=hS ......(1)
where in ΔEOE.,∃.=h=acosθ
Suppose volume of parallelepiped OABCDEF is V.
∴V = Area of □OABC× perpendicular (h) of parallelogram OABC from E
∴V=sh .....(2)
From result (1) and (2)
→a.(→b×→c)=V
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-B ADDITIONAL EXERCISE12videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-B NUMERICAL FROM .DARPAN. BASED ON TEXTBOOK17videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-B NUMERICALS29videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - KUMAR PRAKASHANCHAPTER - QUESTIONS ASKED IN JEE - 2020 EXERCISE - Question16videos
QUESTIONS ASKED IN JEE - 2020
- BOOK - KUMAR PRAKASHANCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks1videos
THERMAL PROPERTIES OF MATTER
Similar Questions
The longest wavelength in Balmer series of hydrogen spectrum will be
02:17View SolutionThe particles of mass m1,m2andm3 are placed on the vertices of an equilateral triangle of sides .a.. Find the centre of mass of this system with respect to the position of particle of mass m1.
 03:11View Solution
03:11View SolutionFind the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are 100g, 150g, and 200g respectively. Each side of the equilateral triangle is 0.5m long.
03:23View SolutionA non-isotropic solid metal cube has coefficient of linear expansion as 5×10−5/∘C along the x-axis and 5×10−6/∘C along y-axis and z-axis. If the coefficient of volumetric expansion of the solid is n×10−6/∘C then the value of n is....
05:17View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
05:24View SolutionShow that if →A.(→B×→c)=0, then →A,→B and →c are coplanar .
03:02View SolutionShow that →a.(→b×→c) is equal in magnitude to the volume of the parallelpiped formed by the vectors →a,→band→c
02:53View SolutionIf the volume of the parallelopiped formed by the vectors →a,→b,→c as three coterminous edges is 27 units, then the volume of the parallelopiped having →α=→a+2→b−→c,→β=→a−→b
and →γ=→a−→b−→c as three coterminous edges, isView Solutionदर्शाइए कि →A.(→B×→C) का परिमाण तीन सदिशों →A,→B एवं →C से बने समांतर षट्फलक के आयतन के बराबर है।
02:58View SolutionIf →a,→b,→c are mutually perpendicular vectors having magnitudes 1,2,3 respectivley, then [→a+→b+→c →b−→a →c]=
00:32View SolutionIf →a,→b,→c are unit vectors such that →a+→b+→c=→o, then the value of →a⋅→b+→b⋅→c+→c⋅→a is -
03:24View SolutionIf →a,→b,→c are three mutually perpendicular vectors and |→a|=∣∣→b∣∣=|→c|=m, then the value of ∣∣→a+→b+→c∣∣ is -
05:58View SolutionThe volume of the tetrahedron formed by the coterminous edges →a,→b,→c is 3. Then the volume of the parallelopiped formed by the coterminous edges →a+→b,→b+→c,→c+→a is
03:55View SolutionvecA+vecB+vec C=0 If so, show that, vecA×vecB=vecB×vec C=vec C×vecA
04:00View SolutionIf three coterminous edges of a parallelopiped are represented by →a−→b,→b−→cand→c−→a, then its volume is :
06:10View Solution
