Question

Shows the shape of a progressive wave at time $t=0$. after a time $t=\left(1\right)/\left(80\right)$, the particle at the origin has its maximum negative displacement.if the wave speed is $80$ units maximum negative displacement. If the wave speed is $80$ units, then find the equation of the progressive wave. .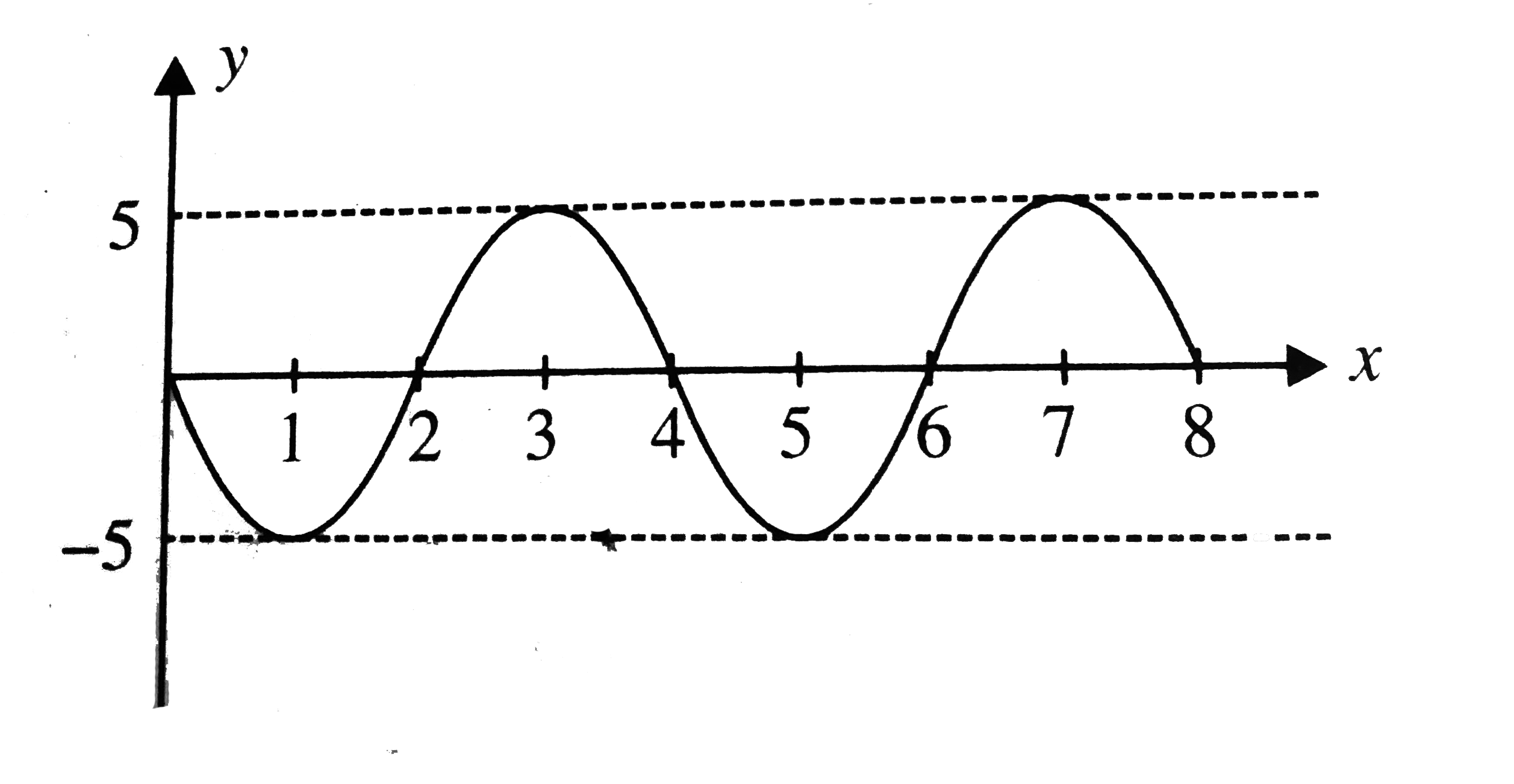

Explanation

The wavelength `lambda=4`
we know, `T=(lambda)/(v)=(4)/(80)=(1)/(20)`
Since after `t=(1)/(80)=(T)/(4)`,the particle at the origin is at its maximum negative, the entire wave pattern would have shifted by a distance of 1 unit `(lambda//4)` to the left.
The wave moves in the negative `x-`axis direction, from this we get `y=A sin[2pi((t)/(t)+(x)/(lambda))+phi]`
we have initially `y=0` for `t=0` and `x=0`
`phi=0,pi,2pi` etc.
Also, `y=-A,` when `t = T//4` and `x=0`
`:. -A=Asin[2pi((1)/(4))+phi]`
`rArr(pi)/(2)+phi=(3pi)/(2),(7pi)/(2)`etc.
or `phi=pi,3pi`,etc.
From Eqs. (i) and (ii), `phi=pi`
Hence `y=5 sin[2pi((t)/(1//20)+(x)/((4)))+pi]`