Six resistors each of 10Ω are connected as shown. The equivalent resistance between points X and Y is

20Ω
5Ω
253Ω
10Ω
The correct Answer is:B

The equivalent circuit of the given network is as shown in the figure.
When a battery is connected between the points X and Y, no current will flow in the arm AB. Then the equivalent circuit will be as shown in figure (a) and (b).

The equivalent resistance between points X and Y is
1Req=120+120+110orReq=5Ω

Topper's Solved these Questions
- CURRENT ELECTRICITY Book:MTG GUIDEChapter:CURRENT ELECTRICITY Exercise:CHECK YOUR NEET VITALS
Explore 16 Videos
- CURRENT ELECTRICITY Book:MTG GUIDEChapter:CURRENT ELECTRICITY Exercise:MCQs AIPMT / NEET
Explore 32 Videos
- CURRENT ELECTRICITY Book:MTG GUIDEChapter:CURRENT ELECTRICITY Exercise:MCQs AIPMT / NEET
Explore 32 Videos
- ATOMS AND NUCLEIBook:MTG GUIDEChapter:ATOMS AND NUCLEIExercise:AIPMT/NEET(MCQs)
Explore 40 Videos
- DUAL NATURE OF MATTER AND RADIATION Book:MTG GUIDEChapter:DUAL NATURE OF MATTER AND RADIATION Exercise:AIPMT/ NEET MCQs
Explore 30 Videos
Similar Questions
Knowledge Check
Six resistors each of 10 ohm are connected shown. The equivalent resistance between points X and Y is
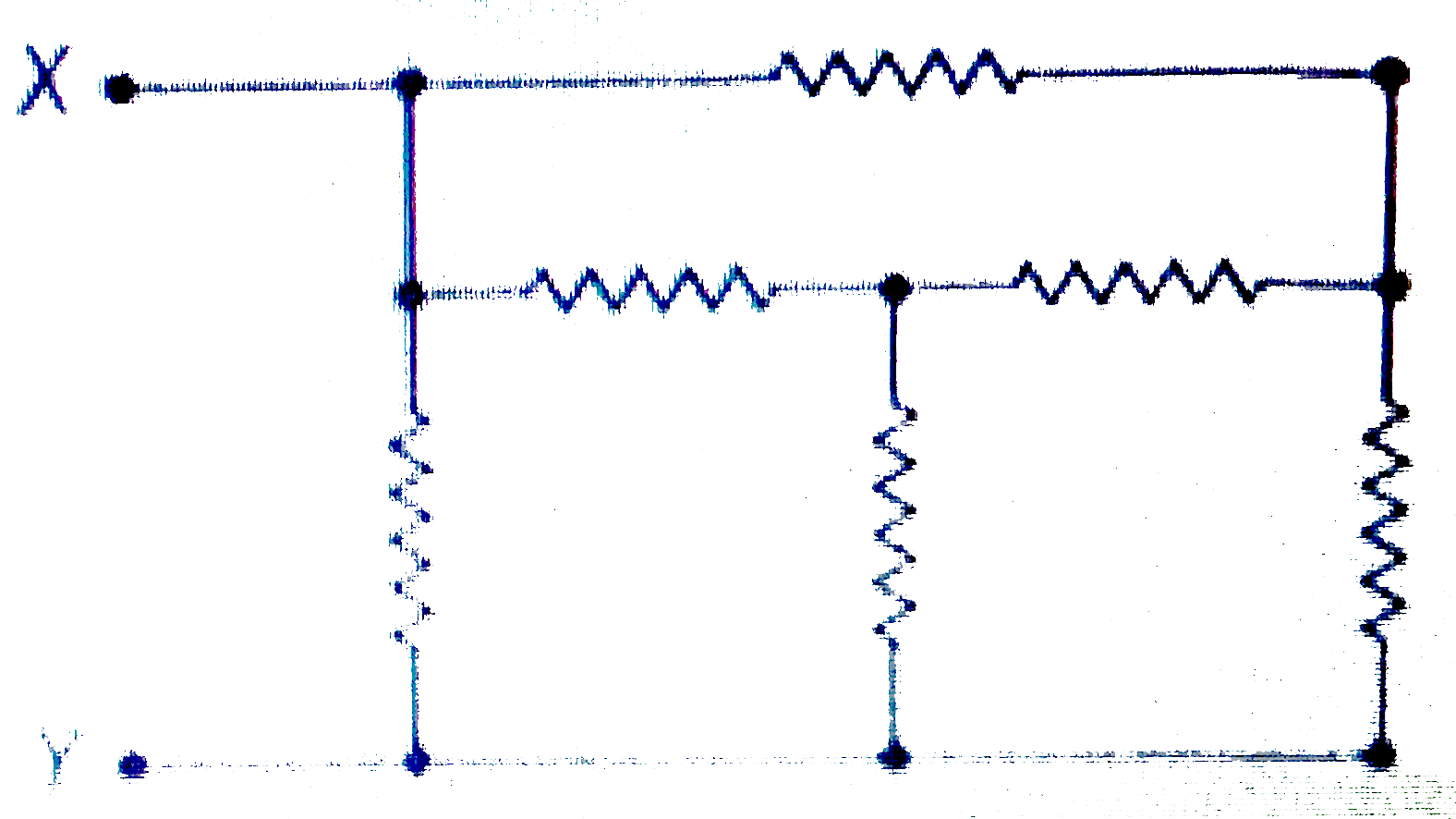 A20ΩB5ΩC25/3ΩD10Ω
A20ΩB5ΩC25/3ΩD10ΩFive resistance, each of 5Ω are connected as shown in figure. Find the equivalent resistance between points (1) A and B , (2) A and C .
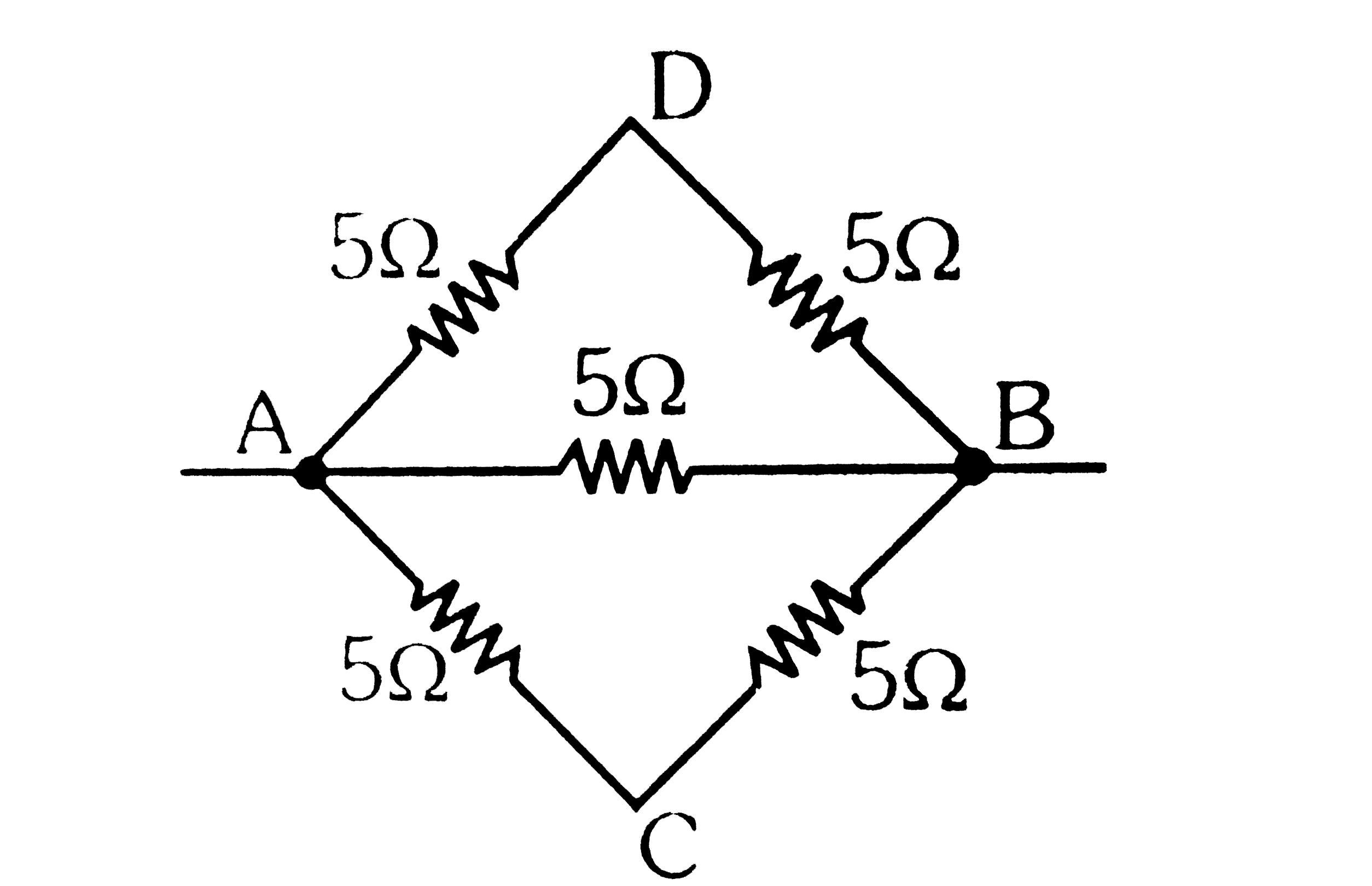 A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5Ω
A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5Ω
Five resistance are connected as shown in the figure. The equivalent resistance between points A and C is
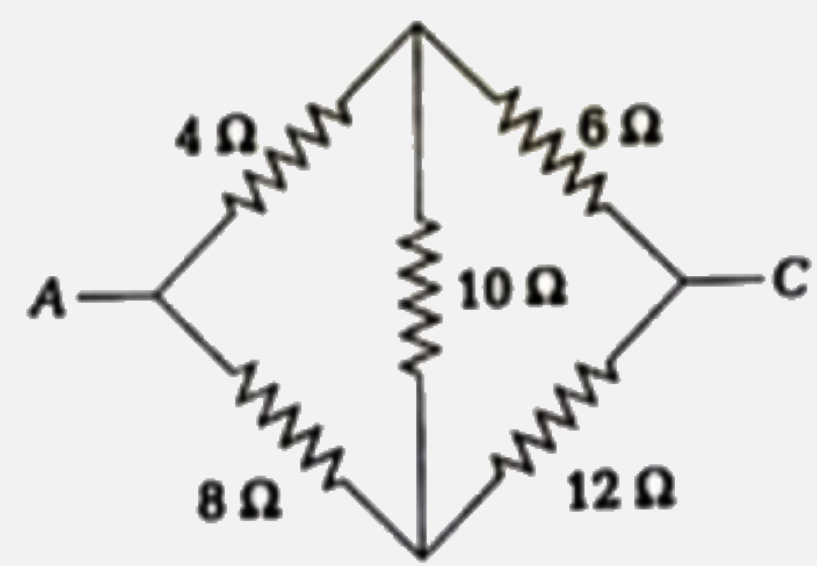
View Solution12 resistors each of 10Ω are connected as shown in the figure. The effective resistance between A and B is
View SolutionFive resistance, each of 5Ω are connected as shown in figure. Find the equivalent resistance between points (1) A and B , (2) A and C .

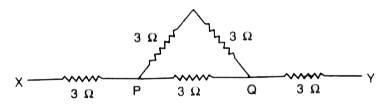
View SolutionFive resistors, each of 3 Ω, are connected as shown in Fig . Calculate the resistance
between the points X and Y.
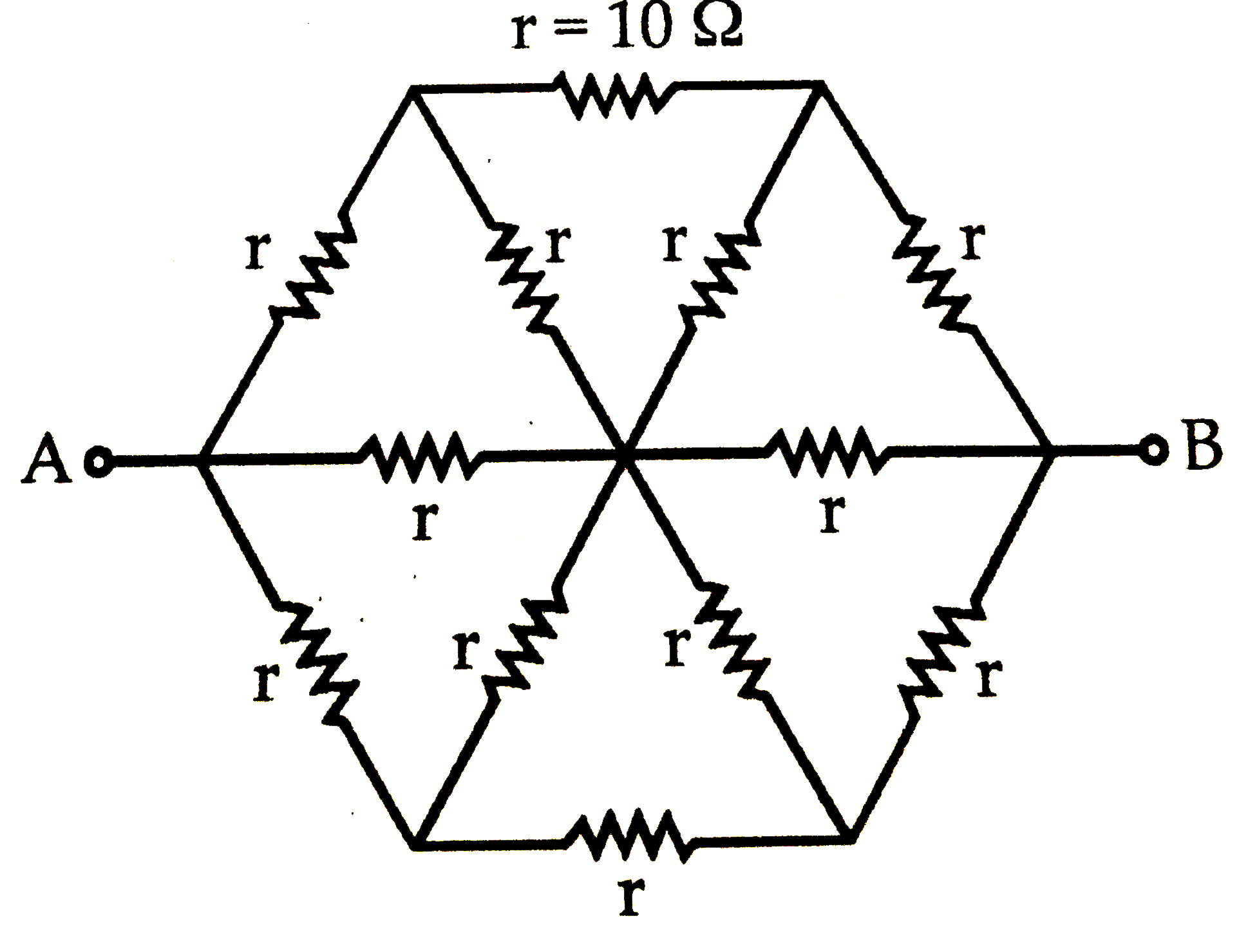
View SolutionSix resistances are connected as shown here.The effective resistance between points A and B is
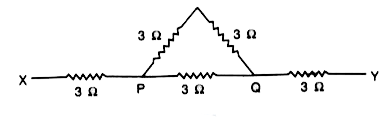
View SolutionFive resistors, each of 3 Ω, are connected as shown in Fig . Calculate the resistance
between the points P and Q,
View Solution
