Question

State and prove Pascal's law.

Explanation

Law : The pressure in a fluid at rest is the same at all points

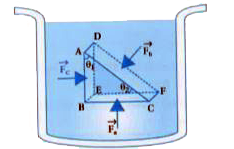
Proof of Pascal.s law. ABC-DEF is an element of the interior of a fluid at rest , This element is in the form of a right angled prism . The element is small so that the effect of gravity can be ignored, but it has been enlarged for the sake of clarity .

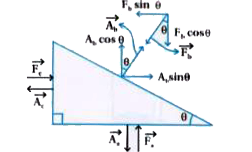
Figure shows an element in the interior of a fluid at rest . This element ABC- DEF is in the form of a right - angled prism.
Area of surface ADFC is `A_(b)`. The force on this surface is `F_(b)` and hence pressure is `P_(b)`.
Area of surface BEFC is `A_(a)` . The perpendicular force on this surface is `F_(a)` and hence pressure is `P_(a)`.
Area of surface ABCD is `A_(c)` .The perpendicular force on this surface is `F_(c)` and hence pressure is `P_(c)`
`F_(a)=F_(b)costheta` (For equilibrium position)
`A_(a)=A_(b)costheta` (by geometry )and
`F_(c)=F_(b)sintheta` (for equilibrium position)
`A_(c)=A_(b)sintheta` (by geometry)
The pressures on rectangular surfaces are as below as shown in figure.
`P_(b)=(F_(b))/(A_(b))` ....(1)
`P_(a)=(F_(a))/(A_(a))=(F_(b)costheta)/(A_(b)costheta)=(F_(b))/(A_(b))` ....(2)
`P_(c)=(F_(c))/(A_(c))=(F_(b)sintheta)/(A_(b)sintheta)=(F_(b))/(A_(b))` ....(3)
It is clear from equation 1,2 and 3
`P_(a)=P_(b)=P_(c)` .... (4)
Equation (4) shows that pressure exerted is same in all directions is a fluid at rest .