State Kirchhoff's rules . Apply Kirchhoff's rules to the loops ACBPA and ACBQA to write the expressions for the currents I1,I2 and I3 in the network .
Step-by-step Solution:
1. State Kirchhoff's Rules:
- Kirchhoff's Current Law (KCL): The sum of currents entering a junction is equal to the sum of currents leaving the junction. Mathematically, it can be expressed as:
Iin=Iout
- Kirchhoff's Voltage Law (KVL): The sum of the electrical potential differences (voltage) around any closed circuit loop is zero. This can be expressed as:
∑V=0
2. Identify the Circuit Elements:
- Let's consider a circuit with resistors and batteries. Assume we have:
- A battery of 6V
- A battery of 10V
- Resistors of 0.5Ω, 1Ω, and 12Ω
- Define the currents as:
- I1: Current through the 0.5Ω resistor
- I2: Current through the 1Ω resistor
- I3: Current through the 12Ω resistor
3. Apply KVL to Loop ACBPA:
- In loop ACBPA, moving in the direction of the current:
- The voltage rise from the 6V battery is positive.
- The voltage drop across the 0.5Ω resistor is 0.5I1 (negative).
- The voltage drop across the 12Ω resistor is 12I3 (negative).
- The KVL equation for loop ACBPA can be written as:
6−0.5I1−12I3=0
- Rearranging gives:
0.5I1+12I3=6(Equation 1)
4. Apply KVL to Loop ACBQA:
- In loop ACBQA, moving in the direction of the current:
- The voltage rise from the 10V battery is positive.
- The voltage drop across the 1Ω resistor is 1I2 (negative).
- The voltage drop across the 12Ω resistor is 12I3 (negative).
- The KVL equation for loop ACBQA can be written as:
10−1I2−12I3=0
- Rearranging gives:
I2+12I3=10(Equation 2)
5. Apply KCL at the Junction:
- At the junction where the currents meet, applying KCL:
- The incoming currents I1 and I2 are positive, and the outgoing current I3 is negative:
I1+I2−I3=0
- Rearranging gives:
I1+I2=I3(Equation 3)
6. Solve the System of Equations:
- Now we have three equations:
- Equation 1: 0.5I1+12I3=6
- Equation 2: I2+12I3=10
- Equation 3: I1+I2=I3
- Substitute Equation 3 into Equations 1 and 2 to find I1 and I2.
7. Substituting and Solving:
- Substitute I3=I1+I2 into Equation 1:
0.5I1+12(I1+I2)=6
- Simplifying gives:
0.5I1+12I1+12I2=6⟹12.5I1+12I2=6(Equation 4)
- Substitute I3=I1+I2 into Equation 2:
I2+12(I1+I2)=10
- Simplifying gives:
I2+12I1+12I2=10⟹12I1+13I2=10(Equation 5)
8. Solve Equations 4 and 5:
- Now solve the two equations:
- Equation 4: 12.5I1+12I2=6
- Equation 5: 12I1+13I2=10
- Use substitution or elimination to find the values of I1 and I2.
9. Final Values:
- After solving the equations, you will get the values for I1, I2, and subsequently I3.
- Kirchhoff's Current Law (KCL): The sum of currents entering a junction is equal to the sum of currents leaving the junction. Mathematically, it can be expressed as:
Iin=Iout
- Kirchhoff's Voltage Law (KVL): The sum of the electrical potential differences (voltage) around any closed circuit loop is zero. This can be expressed as:
∑V=0
- Let's consider a circuit with resistors and batteries. Assume we have:
- A battery of 6V
- A battery of 10V
- Resistors of 0.5Ω, 1Ω, and 12Ω
- Define the currents as:
- I1: Current through the 0.5Ω resistor
- I2: Current through the 1Ω resistor
- I3: Current through the 12Ω resistor
- In loop ACBPA, moving in the direction of the current:
- The voltage rise from the 6V battery is positive.
- The voltage drop across the 0.5Ω resistor is 0.5I1 (negative).
- The voltage drop across the 12Ω resistor is 12I3 (negative).
- The KVL equation for loop ACBPA can be written as:
6−0.5I1−12I3=0
- Rearranging gives:
0.5I1+12I3=6(Equation 1)
- In loop ACBQA, moving in the direction of the current:
- The voltage rise from the 10V battery is positive.
- The voltage drop across the 1Ω resistor is 1I2 (negative).
- The voltage drop across the 12Ω resistor is 12I3 (negative).
- The KVL equation for loop ACBQA can be written as:
10−1I2−12I3=0
- Rearranging gives:
I2+12I3=10(Equation 2)
- At the junction where the currents meet, applying KCL:
- The incoming currents I1 and I2 are positive, and the outgoing current I3 is negative:
I1+I2−I3=0
- Rearranging gives:
I1+I2=I3(Equation 3)
- Now we have three equations:
- Equation 1: 0.5I1+12I3=6
- Equation 2: I2+12I3=10
- Equation 3: I1+I2=I3
- Substitute Equation 3 into Equations 1 and 2 to find I1 and I2.
- Substitute I3=I1+I2 into Equation 1:
0.5I1+12(I1+I2)=6
- Simplifying gives:
0.5I1+12I1+12I2=6⟹12.5I1+12I2=6(Equation 4)
- Substitute I3=I1+I2 into Equation 2:
I2+12(I1+I2)=10
- Simplifying gives:
I2+12I1+12I2=10⟹12I1+13I2=10(Equation 5)
- Now solve the two equations:
- Equation 4: 12.5I1+12I2=6
- Equation 5: 12I1+13I2=10
- Use substitution or elimination to find the values of I1 and I2.
- After solving the equations, you will get the values for I1, I2, and subsequently I3.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET -III
6 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) [SET -I]
33 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET -I
34 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Knowledge Check
Find the current I1, I2, & I3, in the circuit.
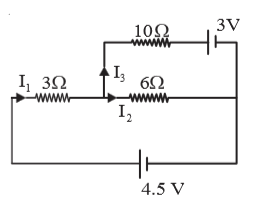 A12,12,1B1,1,2C12,12,3D12,12,0
A12,12,1B1,1,2C12,12,3D12,12,0

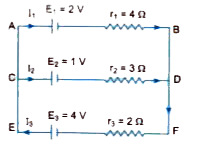
Determine the currents I1,I2andI3 from the network shown in figure.
View SolutionState Kirchhoff's rules. Use these rules to write the expressions for the currents I1,I2 and I3 in the circuit diagram shown in Fig.
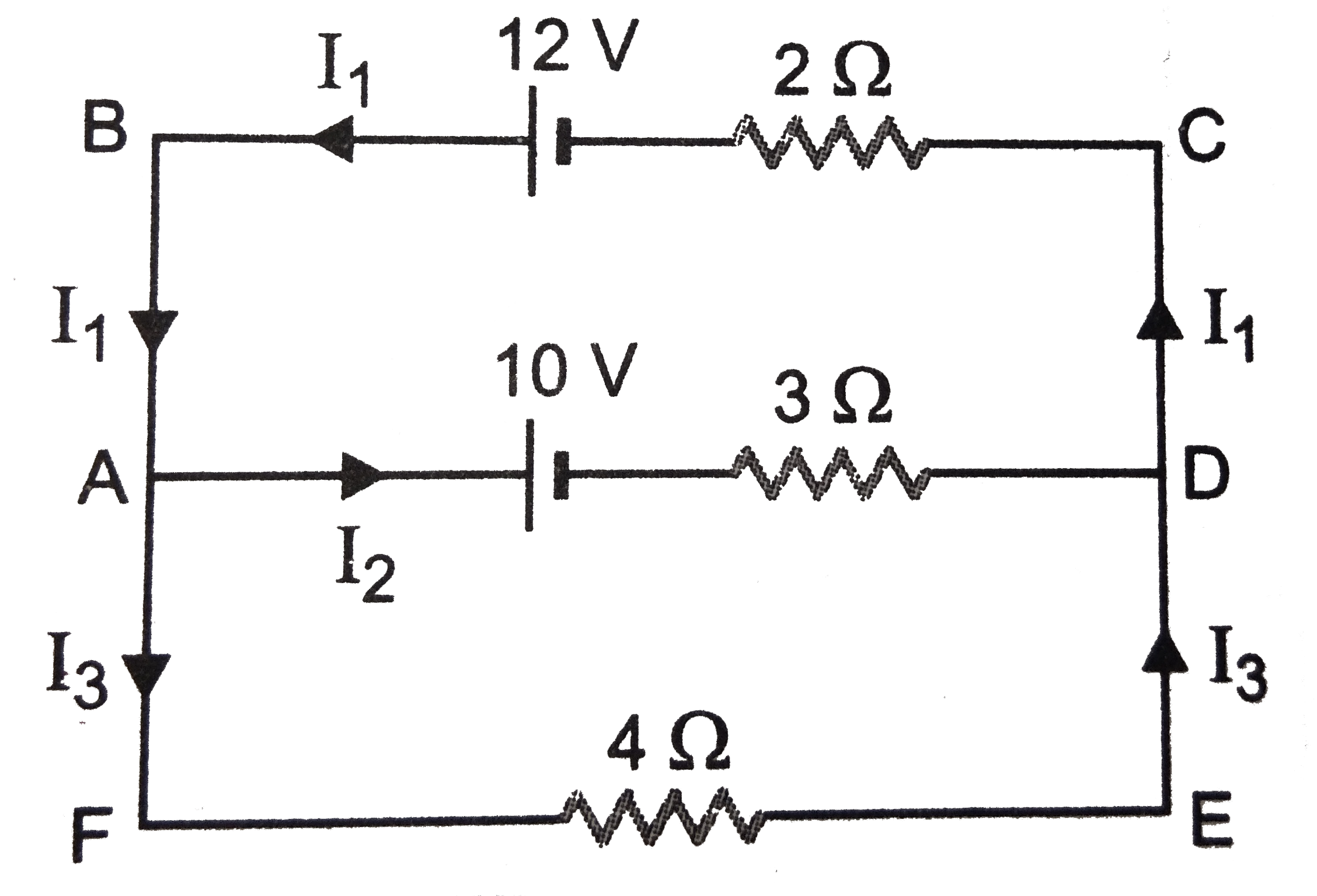
View SolutionUsing kirchhoff's laws, find the currents I1I2 and I3 of the network
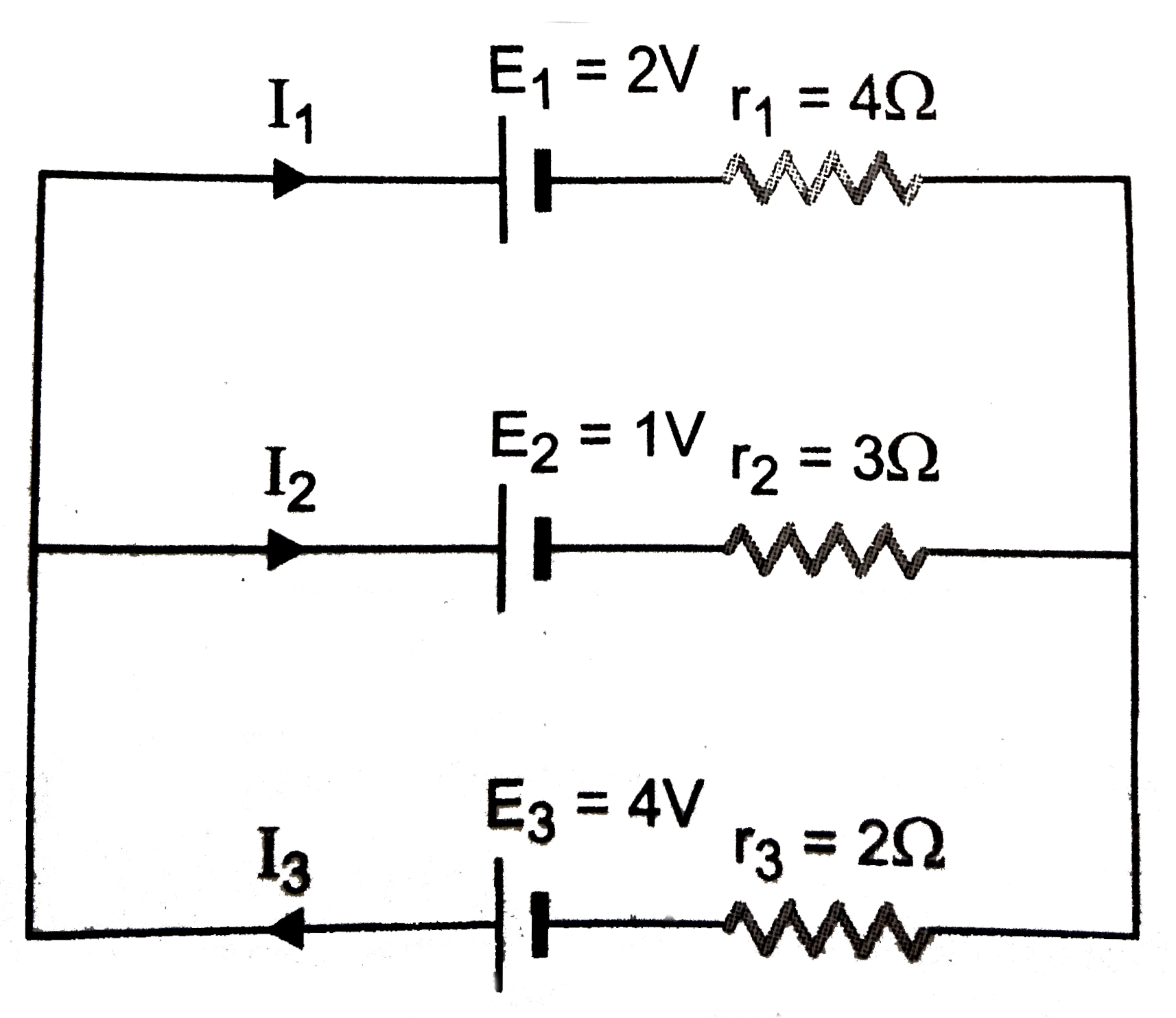
View SolutionUsing kirchhoff's rules wire the experssion for the current I1,I2andI3 in the circuit diagram
View SolutionWhat is Kirchhoff's loop rule.
View SolutionWhat is Kirchhoff's loop rule.
View SolutionThe current I in the network is :

View Solution


