State the approximate value of the critical angle for (a) glass-air surface
(b) water-air surface.
The correct Answer is:(a) 42∘
(b) 49∘.
To find the approximate values of the critical angle for the glass-air surface and the water-air surface, we can follow these steps:
1. Understand the Concept of Critical Angle:
The critical angle is the angle of incidence above which total internal reflection occurs. It can be calculated using the formula:
sin(IC)=1μ
where IC is the critical angle and μ is the refractive index of the medium with respect to air.
2. Determine the Refractive Index for Glass:
The refractive index of glass with respect to air is approximately μglass=43.
3. Calculate the Critical Angle for Glass:
Using the formula for the critical angle:
sin(IC)=1μglass=143=34
Now, calculate IC:
IC=sin−1(34)
Using a calculator, we find:
IC≈48.59∘
Thus, the approximate value of the critical angle for the glass-air surface is 49 degrees.
4. Determine the Refractive Index for Water:
The refractive index of water with respect to air is approximately μwater=32.
5. Calculate the Critical Angle for Water:
Using the formula for the critical angle:
sin(IC)=1μwater=132=23
Now, calculate IC:
IC=sin−1(23)
Using a calculator, we find:
IC≈41.81∘
Thus, the approximate value of the critical angle for the water-air surface is 42 degrees.
Final Answer:
- (a) The approximate value of the critical angle for the glass-air surface is 49 degrees.
- (b) The approximate value of the critical angle for the water-air surface is 42 degrees.
The critical angle is the angle of incidence above which total internal reflection occurs. It can be calculated using the formula:
sin(IC)=1μ
where IC is the critical angle and μ is the refractive index of the medium with respect to air.
The refractive index of glass with respect to air is approximately μglass=43.
Using the formula for the critical angle:
sin(IC)=1μglass=143=34
Now, calculate IC:
IC=sin−1(34)
Using a calculator, we find:
IC≈48.59∘
Thus, the approximate value of the critical angle for the glass-air surface is 49 degrees.
The refractive index of water with respect to air is approximately μwater=32.
Using the formula for the critical angle:
sin(IC)=1μwater=132=23
Now, calculate IC:
IC=sin−1(23)
Using a calculator, we find:
IC≈41.81∘
Thus, the approximate value of the critical angle for the water-air surface is 42 degrees.
- (a) The approximate value of the critical angle for the glass-air surface is 49 degrees.
- (b) The approximate value of the critical angle for the water-air surface is 42 degrees.
Topper's Solved these Questions
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(D) MULTIPLE CHOICE TYPE
3 Videos
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(C) NUMERICALS
3 Videos
- REFRACTION OF LIGHTBOOK - ICSECHAPTER - REFRACTION OF LIGHTEXERCISE - DIAGRAM BASED MCQ:
5 Videos
- REFRACTION THROUGH A LENS BOOK - ICSECHAPTER - REFRACTION THROUGH A LENS EXERCISE - EXERCISE-5(D) (MULTIPLE CHOICE TYPE)
2 Videos
Similar Questions
A glass plate has a thicknes t and refractive index μ. The angle of incidence of a ray from air into the plate is equal to the critical angle for glass air intrerface. The lateral shift (perpendicular distance between incident ray and emergent ray) of ray is given by
View SolutionState the approximate speed of ultrasound in air.
View Solution
Knowledge Check
The critical angle for glass-air interface is :
A24∘B48∘C42∘D45∘Critical angle of glass is θ1 and that of water is θ2. The critical angle for water and glass surface would be (μg=3/2,μw=4/3)
Aless than θ2Bbetween θ1 and θ2Cgreater than θ2Dless than θ1Critical angle of glass is θ1 and that of water is θ2. The critical angle for water and glass surface would be (μg=3/2,μw=4/3)
Abetween θ1 and θ2Bgreater than θ2Cless than θ1Dless than θ2
Figure alongside shows two rays A and B travelling from water to air. If the critical angle for water-air surface is 48∘, complete the ray
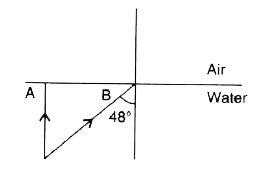
diagram showing the refracted for each. State conditions when the ray will suffer total internal reflection.
View SolutionFigure shows a point source P inside a water container. Three rays A,B and C starting from the source P are shown up to the water surface.
(a) show in the diagram the path of these rays after striking the water surface. The critical angle for water-air surface is 48∘. (b) Name the phenomenon which the rays A, B and C exhibit.
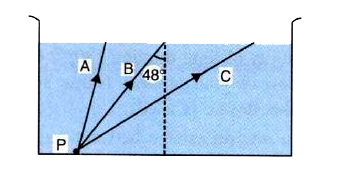 .
.
View Solution(a) Figure below shows a parallel beam of monochromatic light incident on a convex sperical surface, radius of curvature R=30 cm, which separates glass (refractive). Find the distance of image formed.
(b) A ray of light which is incident in air on the surface of a glass block is deviated through 15∘. The angle of incidence in air is 60∘. what is the angle of refraction in glass ? Also, claculate the critical angle for a glass-air interface.
View SolutionThe diagram below shows a point source P inside a water container. Four rays A, B, C, D starting from the source P are shown up to the water surface.

Show in the diagram the path of these rays after striking the water surface. The critical angle for water air surface is 48∘.
View SolutionWater drops stick to a glass surface due to
View Solution
