State the law of radioactive decay. If N0 is the number of radioactive nuclei in the sample at some initial time t0, find out the relation to determine the number N present at a subsequent time.
Step-by-Step Solution
1. Understanding Radioactive Decay:
The law of radioactive decay states that the rate of decay of a radioactive substance is directly proportional to the number of undecayed nuclei present at that time. This can be mathematically expressed as:
dNdt=−λN
where:
- N is the number of radioactive nuclei at time t,
- λ is the decay constant (a positive value that characterizes the rate of decay).
2. Setting Up the Differential Equation:
Rearranging the equation gives us:
dNN=−λdt
3. Integrating Both Sides:
We integrate both sides. The left side integrates with respect to N and the right side with respect to t:
∫dNN=−λ∫dt
This results in:
lnN=−λt+C
where C is the integration constant.
4. Finding the Integration Constant:
To find the constant C, we use the initial condition. At time t=t0, the number of radioactive nuclei is N0:
lnN0=−λt0+C
Thus, we can express C as:
C=lnN0+λt0
5. Substituting Back:
Substituting C back into the equation gives:
lnN=−λt+lnN0+λt0
6. Exponentiating Both Sides:
To solve for N, we exponentiate both sides:
N=e−λt+lnN0+λt0
This simplifies to:
N=N0e−λ(t−t0)
7. Final Relation:
Therefore, the number of radioactive nuclei N present at a subsequent time t can be expressed as:
N=N0e−λt′
where t′=t−t0 is the elapsed time since t0.
The law of radioactive decay states that the rate of decay of a radioactive substance is directly proportional to the number of undecayed nuclei present at that time. This can be mathematically expressed as:
dNdt=−λN
where:
- N is the number of radioactive nuclei at time t,
- λ is the decay constant (a positive value that characterizes the rate of decay).
Rearranging the equation gives us:
dNN=−λdt
We integrate both sides. The left side integrates with respect to N and the right side with respect to t:
∫dNN=−λ∫dt
This results in:
lnN=−λt+C
where C is the integration constant.
To find the constant C, we use the initial condition. At time t=t0, the number of radioactive nuclei is N0:
lnN0=−λt0+C
Thus, we can express C as:
C=lnN0+λt0
Substituting C back into the equation gives:
lnN=−λt+lnN0+λt0
To solve for N, we exponentiate both sides:
N=e−λt+lnN0+λt0
This simplifies to:
N=N0e−λ(t−t0)
Therefore, the number of radioactive nuclei N present at a subsequent time t can be expressed as:
N=N0e−λt′
where t′=t−t0 is the elapsed time since t0.
Topper's Solved these Questions
- ATOMS AND NUCLEIBOOK - PRADEEPCHAPTER - ATOMS AND NUCLEIEXERCISE - Questions Long 11
1 Videos
- ATOMS AND NUCLEIBOOK - PRADEEPCHAPTER - ATOMS AND NUCLEIEXERCISE - Questions Long 12
1 Videos
- ATOMS AND NUCLEIBOOK - PRADEEPCHAPTER - ATOMS AND NUCLEIEXERCISE - Questions Long 9
1 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
Similar Questions
Show that the decay rate R of a sample of radionuclide is related to the number of radioactive nuclei N at the same instant by the expression R=λN.
View SolutionThe rate at which a particular decay process occurs in a radio sample, is proportional to the number of radio active nuclei present . If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN. Consider radioactive decay of A to B which may further decay either to X or to Y, λ1,λ2andλ3 are decay constants for A to B decay , B to X decay and B of Y decay respectively. if at t=0 number of nuclei of A,B , X and Y are N0,N0,zero and zero respectively
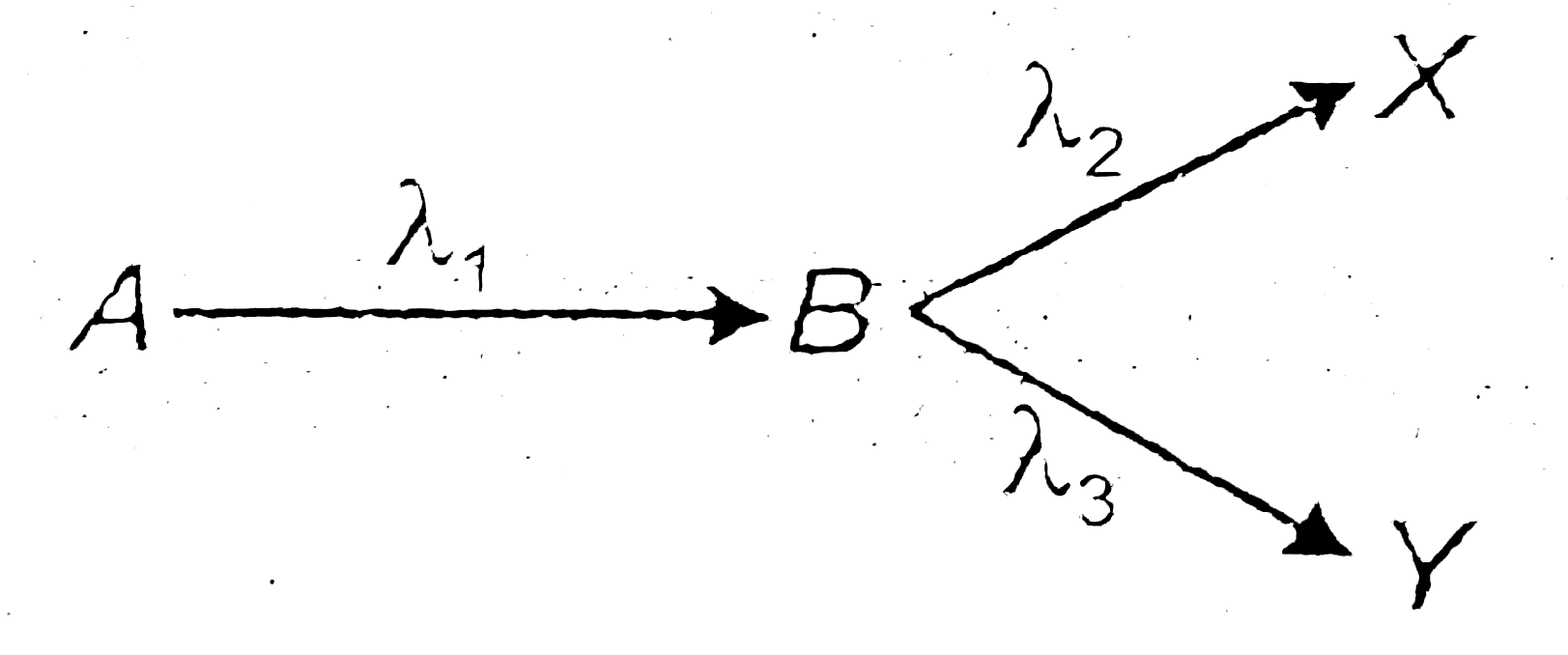
and N1,N2,N3,N4 are number of nuclei A,B , X and Y at any instant.
The number of nuclei of B will first increase then after a maximum value, it will decreases, if
View Solution
Knowledge Check
If N0andN are the number of radioactive particles at time t=0andt=t, then
Aλ=1tlogN0NBλ=2.303tlogNN0Cλ=t2.303logN0NDλ=2.303tlogN0NIf N0 is the number of radioactive nuclei initially present , then the number of nuclei remaining undecayed at the end of nth half life is
A2−nN0B2−nN0C2−nN0D2−nN0Let T be the mean life of a radioactive sample. 75% of the active nuclei present in th sample initially will deacy in time
A2TB1/2(ln2)TC4TD2(ln2)T
The rate at which a particular decay process occurs in a radio sample, is proportional to the number of radio active nuclei present . If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN. Consider radioactive decay of A to B which may further decay either to X or to Y, λ1,λ2andλ3 are decay constants for A to B decay , B to X decay and B of Y decay respectively. if at t=0 number of nuclei of A,B , X and Y are N0,N0,zero and zero respectively

and N1,N2,N3,N4 are number of nuclei A,B , X and Y at any instant.
At t=∞, which of the following is incorrect ?
View SolutionThe rate at which a particular decay process occurs in a radio sample, is proportional to the number of radio active nuclei present . If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN. Consider radioactive decay of A to B which may further decay either to X or to Y, λ1,λ2andλ3 are decay constants for A to B decay , B to X decay and B of Y decay respectively. if at t=0 number of nuclei of A,B , X and Y are N0,N0,zero and zero respectively

and N1,N2,N3,N4 are number of nuclei A,B , X and Y at any instant.
Rate of accumulation of B of any instant will be
View SolutionA radioactive substance has half-life T12 and number of radioactive nuclides present initially was N0. What is the number of radioactive nuclides at time t ?
View SolutionFor a radioactive sample, at given instant, number of active nuclei is N and its decay constant is λ then the incorrect relation is–
View SolutionFor any radioactive sample number of nuclei undergoing the decay per unit time is proportional to
View Solution
