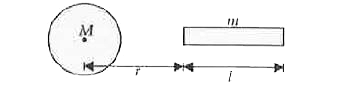
Statement I: The force of gravitation between a sphere and a rod of mass $M_{2}$ is $= (G M_{1} M_{2}) / r$ .
Statement II: Newton's law of gravitation holds correct for point masses.

Statement I is True, Statement II is True: Statement II is a correct explanation for Statement I.

Statement I is True, Statement II is True: Statement II is Not a correct explanation for Statement I.

Statement I is True, Statement II is False.

Statement I is False, Statement II is True.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Assertion : The centres of two cubes of masses $m_{1} and m_{2}$ are separated by a distance r. The gravitational force between these two cubes will be $\frac{G m_{1} m_{2}}{r^{2}}$
Reason : According to Newton's law of gravitation, gravitational force between two point masses $m_{1} and m_{2}$ separated by a distance r is $\frac{G m_{1} m_{2}}{r^{2}}$ .
AIf both Assertin and Reason are correct and Reason is the correct explanation of Assertion
BIf both Assertion and Reason are correct but Reason is not the correct explanation of Assertion
CIf Assertion is true but Reason is false
DIf Assertion is false but Reason is true
The force of gravitation between two bodies of mass 2 kg each separated by a distance of 2 m in vacuum is
A $6.67 \times 10^{- 11} N$
B $6.67 \times 10^{- 10} N$
C $6.67 \times 10^{- 9} N$
Dnone of these
Statement-1 : Two soild sphere of radius $r$ and $2 r$ , made of same material, are kept in contact. The mutual grvitational force to attraction between them is proportional to $1 / r^{4}$ .
Statement-2 : Gravitational attraction between two point mass bodies varies inversely as the square of the distance between them.
AStatement -1 is true , Statement -2 is true , Statement-2 is a correct explanation of Statement -1.
BStatement -1 is true , Statement-2 is true , Statement-2 is a correct explanation of Statement-1.
CStatement-1 is true , Statement-2 is false.
DStatement-1 is false , Statement-2 is true.