Suppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point a distance h directly above the tunnel. The motion of the particle as seen from the earth is
(i), (ii)
(i), (iii)
(ii), (iii)
(iii), (iv)
The correct Answer is:D
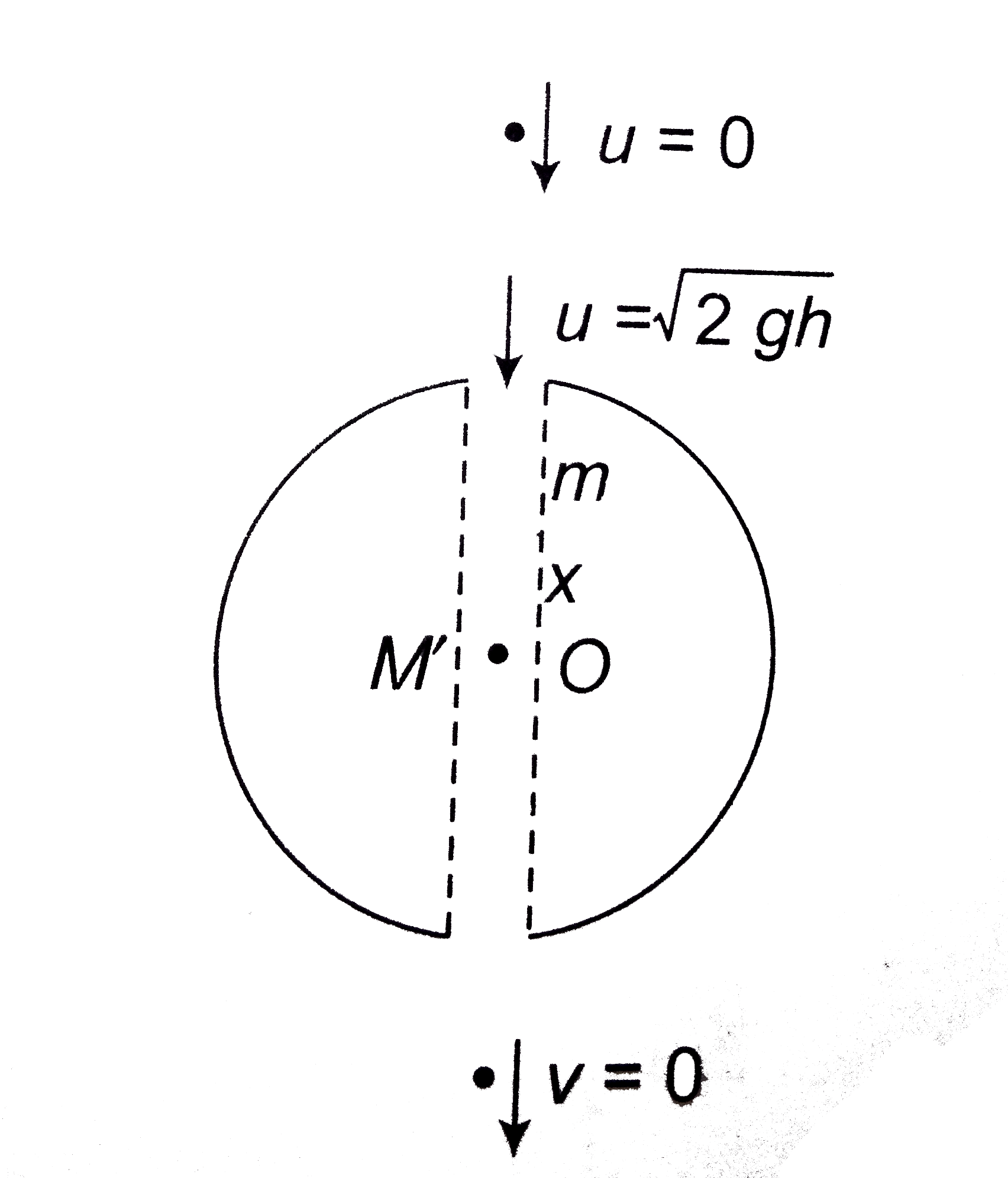
Force outside tunnel is not proportional to displacement hence, no SHM.
Topper's Solved these Questions
Similar Questions
A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.

View Solution
Knowledge Check
If a tunnel is dug along the diameter of the earth and a ball is dropped into the tunnel, it will have
Alinear motionBcircular motionCoscillatory motionDtranslatory motionIf a tunnel is dug along the diameter of earth and a piece of stone is dropped into it, then the stone will
Acome out of the another end of earth and will excape out in spaceBcome to rest at the centre of earthCstart oscillating about the centre of the earthDstop at another end of earthA hole is drilled along the diameter of the earth and pen is dropped into it. The time taken by it is reach other end of the earth is
A162.2 minB84.6 minC21.2 minD42.3 min
Imagine a tunnel dug along a diameter of the earth. Show that a particle dropped from one end of the tunnel executes simple harmonic motion. What is the time period of this motion? Assume the earth to be a sphere of uniform mass density (equal to its known average density=5520 kg m−3.)G=6.67×10−11Nm2kg−2.Neglect all damping forces.
View SolutionA tunnel is dug along a diameter of the planet. A particle is dropped into it at the surface. The particle reaches the centre of the planet with speed v. If ve is the escape velocity from the surface fo the planet, then-
View SolutionA tuning is dug along the diameter of the earth. There is particle of mass m at the centre of the tunel. Find the minimum velocity given to the particle so that is just reaches to the surface of the earth. (R= radius of earth)
View SolutionA tunnel is dug across the diameter of earth. A ball is released from the surface of Earth into the tunnel. The velocity of ball when it is at a distance R2 from centre of earth is (where R = radius of Earth and M = mass of Earth)
View SolutionSuppose a smooth tunnel is dug along a straight line joining two points on the surface of the earth and a particle is dropped from rest at its one end. Assume that mass of the earth is uniformly distributed over its volume. Then, which of the following statements are not correct?
View Solution