Suppose that at time t>––––0 the position of a particle moving on the x-axis is x=(t−1)(t−4)4m.
(a) When is the particle at rest ?
(b) During what time interval does the particle move to the left ?
(c) Find maximum velocity of particle while moving to the left.
(a)dxdt=(t−4)4+4(t−4)3(t−1)=0
∴ (t−4)3[t−4+4t−4]=0
⇒ t=4sort=85s
(b) dxdt<0⇒(t−4)3(5t−8)<0
For this , t<4
and t>85
⇒ t∈(85,4)
(c) Particle will be faster when (dxdt) is maximum
∴ ddt(dxdt)=0
∴ d2xdt2=3(t−4)2(5t−8)+5(t−4)3=0
⇒ (1−4)2[15t−24+5t−20]=0
⇒ t=4s or t=4420=2.2s
But at t=4sdxdt=0
∴(dxdt) is maximum at t=2.2 s
and maximum value of dxdt=(2.2−4)3(5×2.2−8)
=−17.49m/s
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The position of a particle moving along x-axis is given by x=10t−2t2. Then the time (t) at which it will momentily come to rest is
AZeroB2.5 sC5 sD10 s - Question 2 - Select One
The position (x) of a particle moving along x - axis veries with time (t) as shown in figure. The average acceleration of particle in time interval t = 0 to t = 8 s is
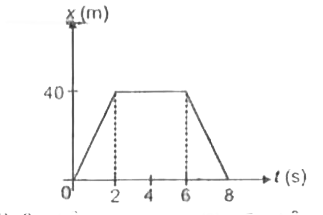 A3m/s2B−5m/s2C−4m/s2D2.5m/s2
A3m/s2B−5m/s2C−4m/s2D2.5m/s2 - Question 3 - Select One
The coordinates of a particle moving in XY-plane very with time as x=4t2,y=2t. The locus of the particle is
AStraight lineBCircleCParabolaDEllipse
The position of particle moving along the x-axis veries with time t as x=6t−t2+4. Find the time-interval during which the particle is moving along the positive x-direction.
View SolutionThe position of a particle moving in XY-plane varies with time t as x=t,y=3t−5.
(i) What is the path traced by the particle?
(ii) When does the particle cross-x-axis?View SolutionThe position of a particle moving along the y-axis is given as y=3t2−t3 where y is in , metres and t is in sec.The time when the particle attains maximum positive y position will be
View Solution(a) The position of a particle moving along the x-axis depends on the time according to equation. x=(3t2−t3) m. At what time does the particle reaches its maximum x-position?
(b) What is the displacement during the first 4s.View SolutionIf the velocity of the a particle moving on x-axis is given by v=3t2−12t+6. at what time is the acceleration of particle zero ?
View Solution

