Suppose the acceleratio due to gravity at thth's surface is 10ms−2 and at the surface of Mars it is 4.0ms−2. A passenger goes from the to the mars in a spacehip with a constant velocity. Neglect all other object in sky. Which part of figure best represent the weight (net gravitational force) of the passenger as a function of time?
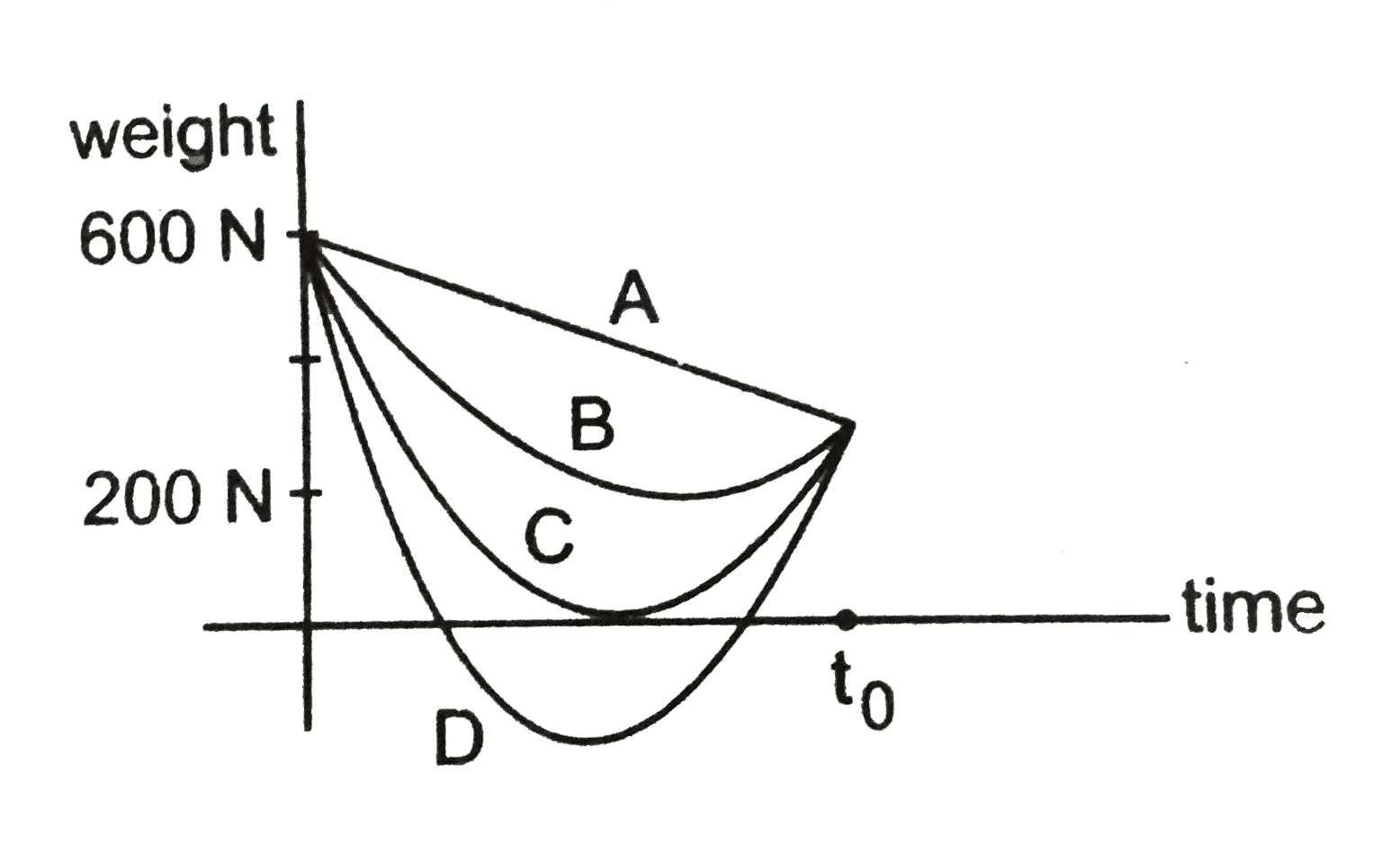
A
B
C
D
The correct Answer is:C
Step by step video, text & image solution for Suppose the acceleratio due to gravity at thth's surface is 10ms^-2 and at the surface of Mars it is 4.0ms^-2. A passenger goes from the to the mars in a spacehip with a constant velocity. Neglect all other object in sky. Which part of figure best represent the weight (net gravitational force) of the passenger as a function of time? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - HC VERMACHAPTER - GRAVITATIONEXERCISE - Objective 2
6 Videos
- GRAVITATIONBOOK - HC VERMACHAPTER - GRAVITATIONEXERCISE - Exercises
39 Videos
- GRAVITATIONBOOK - HC VERMACHAPTER - GRAVITATIONEXERCISE - Short Answer
19 Videos
- FRICTIONBOOK - HC VERMACHAPTER - FRICTIONEXERCISE - Exercises
31 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMACHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
4 Videos
Similar Questions
The acceleration due to gravity on the surface of the earth is 10ms−2 . The mass of the planet . Mars as compared to earth is 1/10 and radius is 1/2 . Determine the gravitational acceleration of a body on the surface on Mars .
View SolutionThe value of acceleration due to gravity at earth's surface is 9.8ms^-1 . The altitude above its surface at which the acceleration due to gravity decreases to 4.9ms^-2 ,is close to (Take,radius of earth =6.4*10^6 m )
View Solution
Knowledge Check
If accleration due to gravity on the surface of earth is 10ms−2 and let acceleration due to gravitational acceleration at surface of another planet of our solar system be 5ms−2 An astronaut weighing 50kg on earth goes to this planet in spaceship with a constant velcity The weight of the astronaut with time of fiight is roughly given by
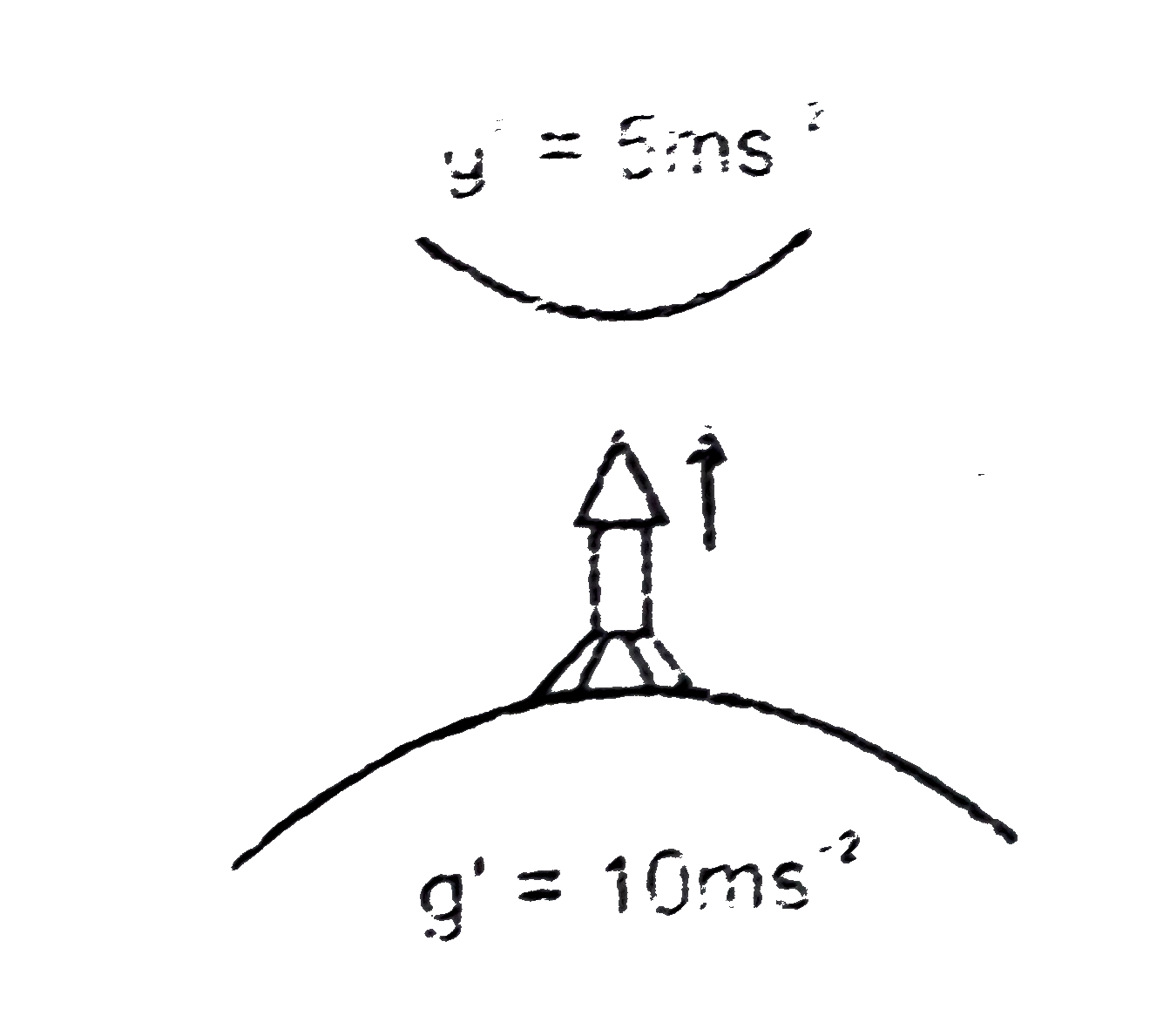 .A
.A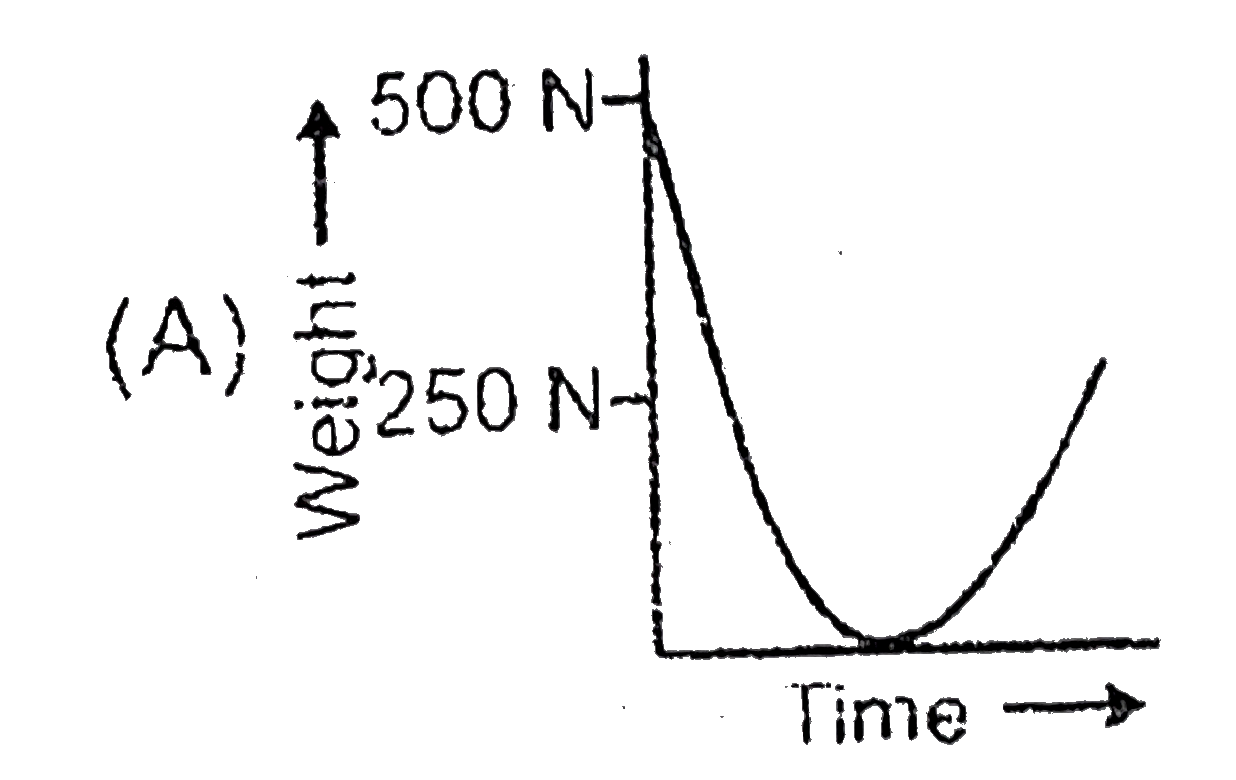 B
B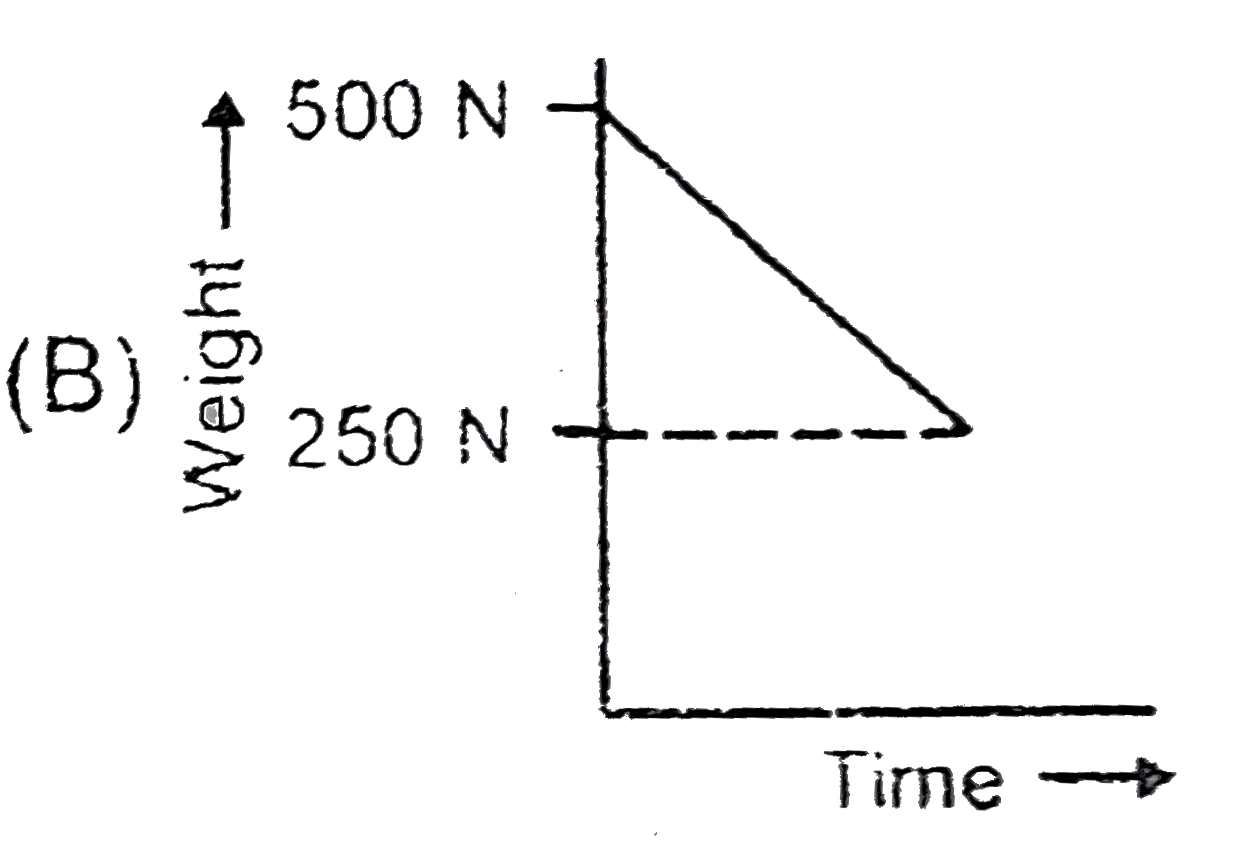 C
C D
D
The value of acceleration due to gravity at earth's surface is 9.8ms−2. The altitude above its surface at which the acceleration due to gravity decreases to , is close to: (radius of earth =6.4×106m)
A2.6×106mB6.4×106mC9.0×106mD1.6×106mAt a point above the surface of the earth, the gravitational potential is −5.12×107JKg−1 and the acceleration due to gravity is 6.4ms−2. Assuming the mean radius of the earth to be 6400 km, calculate the heights of this point above the earth's surface.
A1200 kmB1600 kmC1800 kmD2400 km
The value of acceleration due to gravity at Earth's surface is 9.8ms−2. The altitude (in metre) above its surface at which the acceleration due to gravity decreases to 4.9ms−2, is close to :(Radius of earth =6.4×106m)
View SolutionAt what altitude, the acceleration due to gravity reduces to one fourth of its value as that on the surface of the earth ? Take radius of earth as 6.4×106m, g on the surface of the earth as 9.8ms−2.
View SolutionThe value of acceleration due to gravity at the surface of the earth is 9.8ms−2 and the mean radius is about 6.4×106m. Assuming that we could get more soil some where, estimate how thick would an added uniform outer layer on the earth have to have the value of acceleration due to gravity 10ms−2 exactly ?
View SolutionWhen water is filled caerfully in a glass . One can fill it to a height h above the rim of glass due to the surface tension of water . To calculate h just before water starts flowing model the shape of the water above the rim as a disc of thickness h having semicircular edges as shown achematically in the figure When the pressure of water at the bottom of this disc exceeds what can be withstood due to the surface lension , the water surface breaks near the rim and water starts flowing form there if the density of water, its surface tension and the acceleration due to gravity are 103kgm−3,0.07Nm−1and10ms−2 , respectively, the value of h (in mm) is _________

View Solutiona projectile is fired from the surface of the earth with a velocity of 5ms−1 and angle θ with the horizontal. Another projectile fired from another planet with a velocity of 3ms−1 at the same angle follows a trajectory which is identical with the trajectory of the projectile fired from the earth.The value of the acceleration due to gravity on the planet is in ms−2 is given (g=9.8ms−2)
View Solution
