Suppose the spheres A and B in the above question have identical sizes. A third sphere of the same size but uncharged is brought in contact with the first, then brought in contact with the second, and finally removed from both. What is the new force of repulsion between A and B?
To solve the problem step by step, we will follow the procedure outlined in the video transcript.
Step 1: Calculate the initial force of repulsion between spheres A and B.
Given:
- Charge on each sphere (A and B), Q=6.5×10−7 C
- Distance between the centers of the spheres, R=0.5 m
- Coulomb's constant, K=9×109 N m²/C²
Using Coulomb's law, the force of repulsion F between the two charged spheres can be calculated using the formula:
F=KQ2R2
Substituting the values:
F=9×109(6.5×10−7)2(0.5)2
Calculating F:
F=9×109(4.225×10−13)0.25=9×109×1.69×10−12=1.5×10−2 N
Step 2: Determine the charge on sphere A after contact with the uncharged sphere C.
When sphere C (uncharged) comes into contact with sphere A:
- Charge on A before contact = Q
- Charge on C before contact = 0
The total charge after contact is:
Total charge=Q+0=Q
Since they are identical spheres, the charge will be equally distributed:
Charge on A after contact=Charge on C after contact=Q2
Step 3: Determine the charge on sphere B after contact with sphere C.
Now, sphere C (with charge Q2) comes into contact with sphere B:
- Charge on B before contact = Q
- Charge on C before contact = Q2
The total charge after contact is:
Total charge=Q+Q2=3Q2
Again, the charge will be equally distributed:
Charge on B after contact=Charge on C after contact=3Q4
Step 4: Calculate the new force of repulsion between spheres A and B.
Now, we have:
- Charge on A = Q2
- Charge on B = 3Q4
Using Coulomb's law again for the new force F′:
F′=KQA⋅QBR2=K(Q2)⋅(3Q4)R2
F′=K3Q28R2
Substituting the values:
F′=38⋅9×109(6.5×10−7)2(0.5)2
Calculating F′:
F′=38⋅9×109⋅1.69×10−12=5.7×10−3 N
Final Answer:
The new force of repulsion between spheres A and B is 5.7×10−3 N.
---
- Charge on each sphere (A and B), Q=6.5×10−7 C
- Distance between the centers of the spheres, R=0.5 m
- Coulomb's constant, K=9×109 N m²/C²
F=KQ2R2
F=9×109(6.5×10−7)2(0.5)2
F=9×109(4.225×10−13)0.25=9×109×1.69×10−12=1.5×10−2 N
- Charge on A before contact = Q
- Charge on C before contact = 0
Total charge=Q+0=Q
Since they are identical spheres, the charge will be equally distributed:
Charge on A after contact=Charge on C after contact=Q2
- Charge on B before contact = Q
- Charge on C before contact = Q2
Total charge=Q+Q2=3Q2
Again, the charge will be equally distributed:
Charge on B after contact=Charge on C after contact=3Q4
- Charge on A = Q2
- Charge on B = 3Q4
F′=KQA⋅QBR2=K(Q2)⋅(3Q4)R2
F′=K3Q28R2
F′=38⋅9×109(6.5×10−7)2(0.5)2
Calculating F′:
F′=38⋅9×109⋅1.69×10−12=5.7×10−3 N
The new force of repulsion between spheres A and B is 5.7×10−3 N.
Similar Questions
Two insulated identically sized charged copper spheres A and B have their centers separated by a distance of 50 cm. A third sphere of the same size but uncharged is brought in contact with the first, then in contact with the second and finally removed from both. What is the new force of repulsion between A and B?
View SolutionTwo spherical conductors B and C having equal radii and cayying equal charges on them repel each other with a force F when kept apart at some distance. A third spherical conductor having same radius as that B but uncharged is brought in contact with B, then brought in contact with C and finally removed away from both. The new force of repulsion between B and C is
View Solution
Knowledge Check
- Question 1 - Select One
Two spherical conductors B and C having equal radii and cayying equal charges on them repel each other with a force F when kept apart at some distance. A third spherical conductor having same radius as that B but uncharged is brought in contact with B, then brought in contact with C and finally removed away from both. The new force of repulsion between B and C is
AF/4B3F/4CF/8D3F/8
Two identical conducting spheres 1 and 2 carry equal amounts of charge and are ficed apart at a certain distance larger than their diameters. The spheres repel each other with an electrical force of 88mN. A thired identical sphere 3, having an insulating handle and initially uncharged, is touched first to sphere 1 and then to sphere 2 and finally removed. Find the force between spheres 1 and 2 as shown if Figure.
 ,View Solution
,View SolutionFrom a sphere of electrical conductivity K two planes cut a piece such that first plane passes through the centre of sphere and second parallel to first one at distance R/2 from centre then resistance between A and B
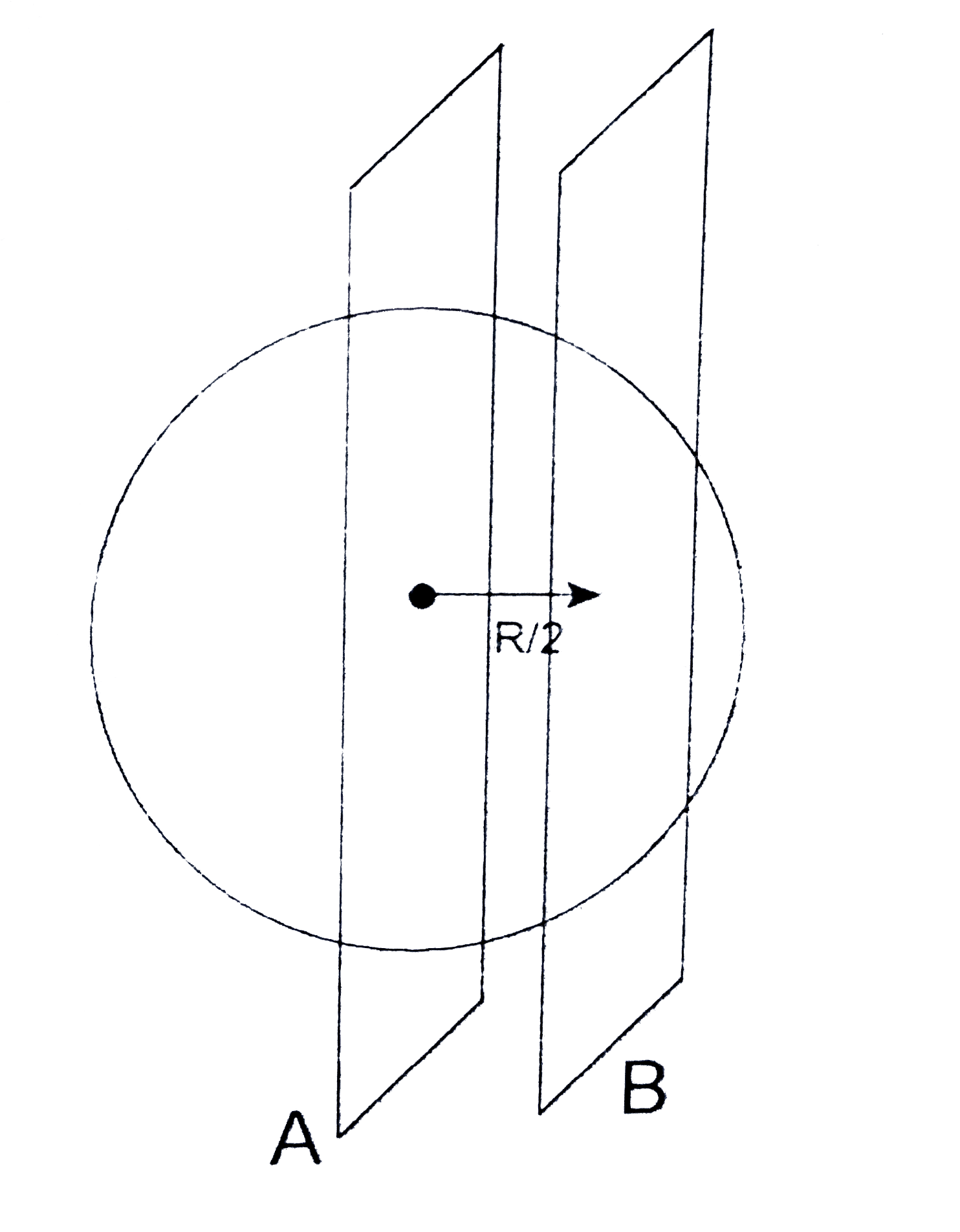 View Solution
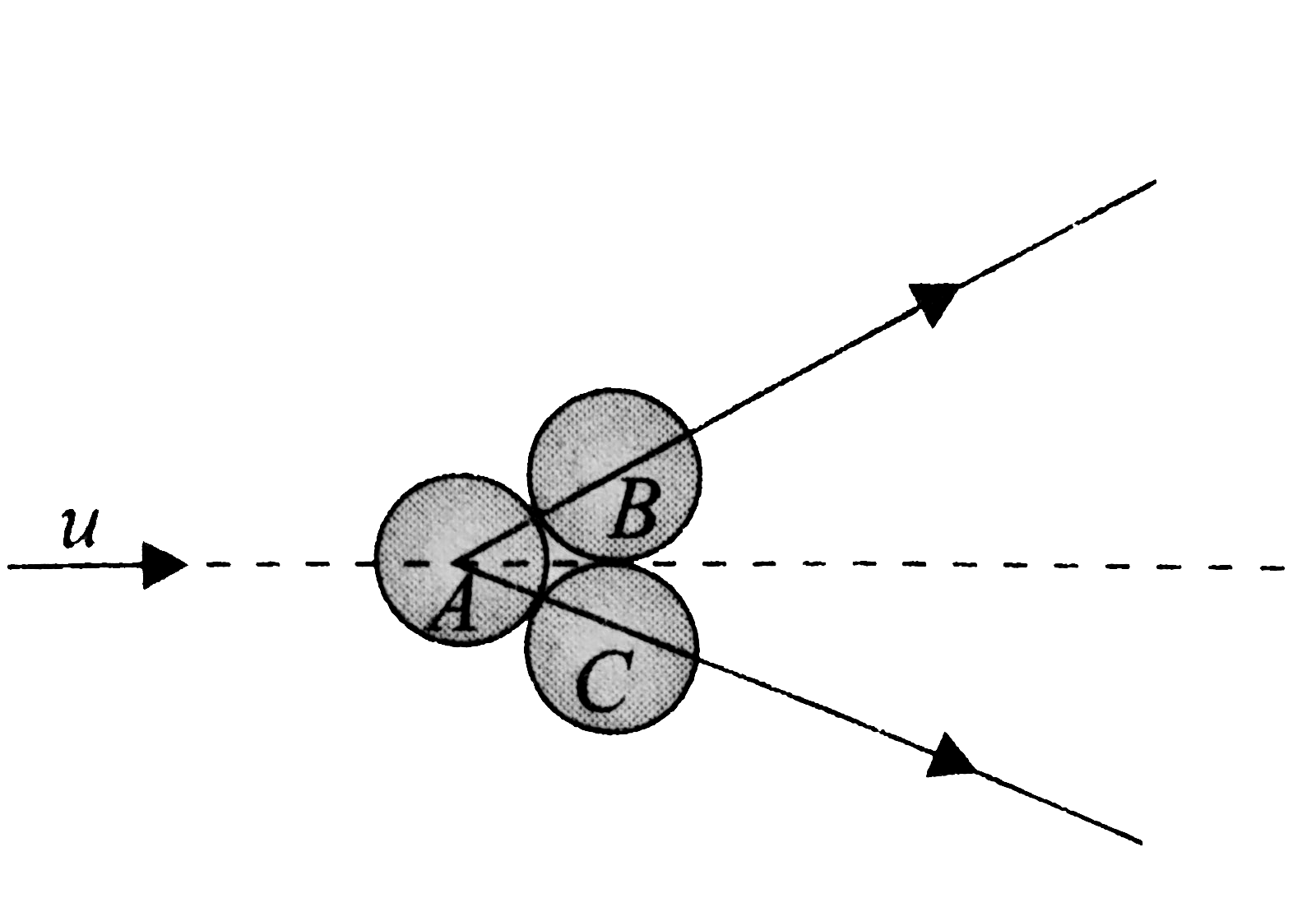
View SolutionTwo equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.
The coefficient of restitution between the two spheres A and B (or between A and C) isView SolutionTwo identical conducting balls A and B have charges- Q and + 3Q respectively. They are brought in contact with each other and then separated by a distance d part. Find the nature of the Coulomb force between them.
View SolutionTwo equally charged, indentical metal spheres A and B repel each other with a force F. The spheres are kept fixed with a distance r between them. A third identical, but uncharged sphere C is brought in contact with A and removed. The magnitude of the net electric force on A is
View SolutionTwo equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.
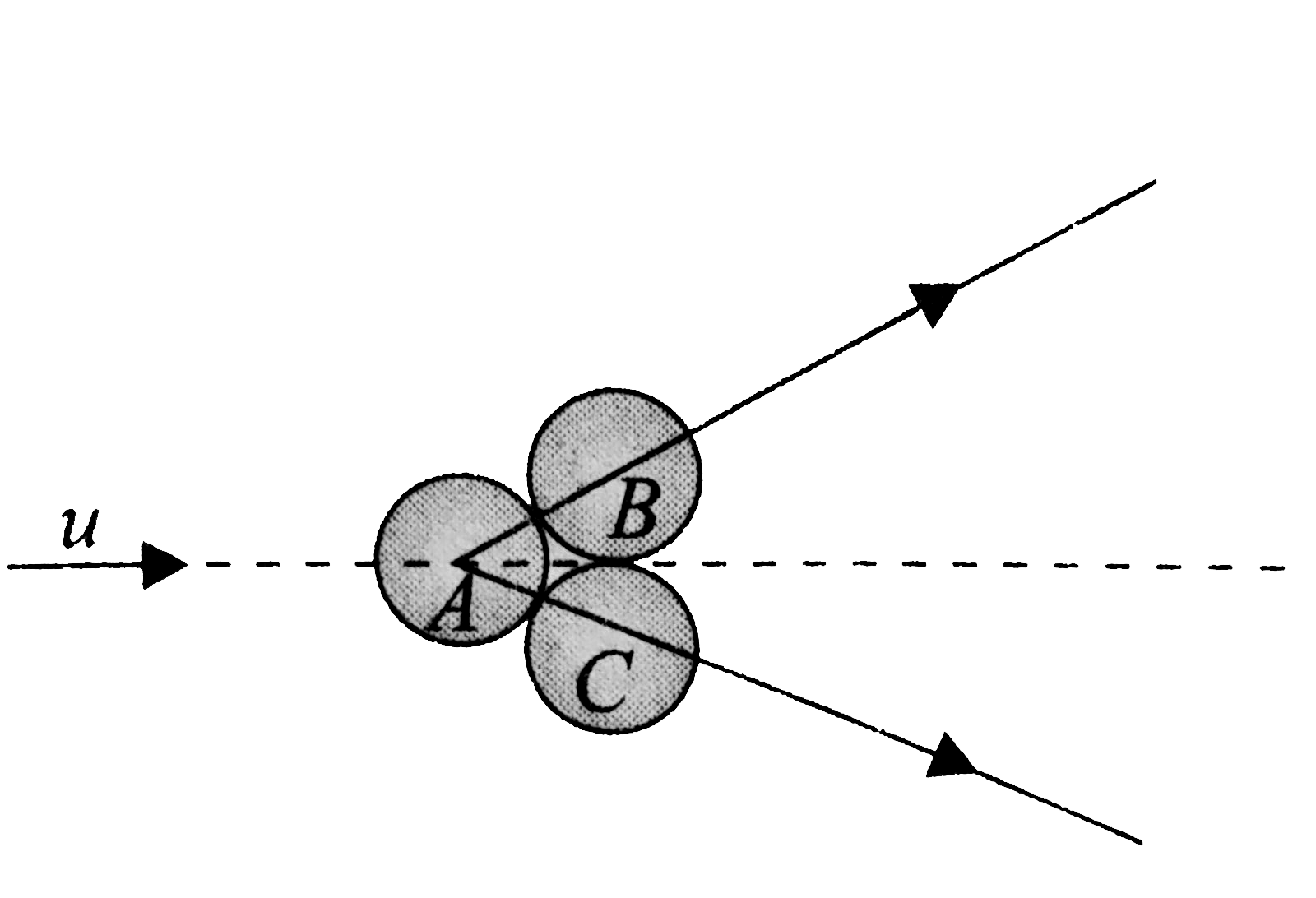
Find the velocity acquired by each of the spheres B and C after collision.View SolutionTwo identical conduction spheres, one having an initial charge +Q and the other initially uncharged, are brought into contact.
(a) What is the new charge on each sphere?
(b) While the spheres are in contact, a positively chaged rod is moved close to one sphere, causing a redistribution of hte charges on the two spheres so the charge on hte sphere closest to the rod has a charge-Q. What is the charge to the other sphere?View Solution

