The absorpotion transitions between the first and the fourth energy states of hydrogen atom are 3. The emission transitions between these states will be
3
6
5
4
The correct Answer is:B
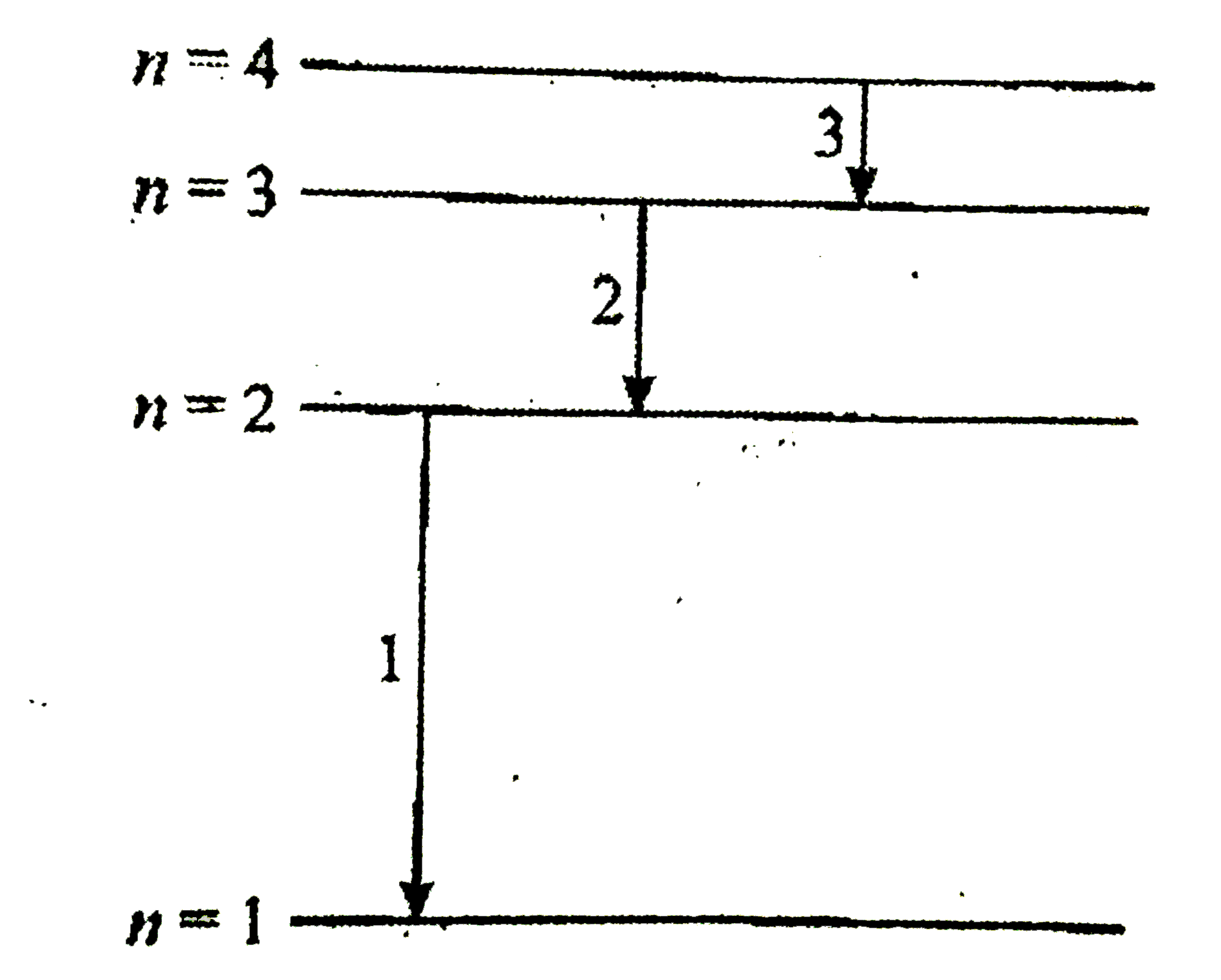
There are six emission transitions.
4→3,4→2,4→1
3→2,3→1 and 2→1

No. of transitions =n(n−1)2=4×32=6
Topper's Solved these Questions
Similar Questions
Knowledge Check
A transition state represents a transition between the
Aproducts and the activated complexBreactants and the activated complexCreactants and the productsDreactants and the intermdiatesThe wavelengths of the lines emitted in the Lyman series of the spectrum of hydrogen atom correspond to transitions between energy levels with total quantum numbers
An =3 to n=1Bn =3 to n=2Cn=4 to n=1Dn=4 to n=2The wavelengths of the lines emitted in the Lyman series of the spectrum of hydrogen atom correspond to transitions between energy levels with total quantum numbers
An =3 to n=1Bn =3 to n=2Cn=4 to n=1Dn=4 to n=2
An electron has been excited from first to fourth energy state in an atom. What are the possible transitions when the electron come back to the ground state ?
View SolutionFigure represents transitions of electrons from higher to lower state of a hydrogen atom. Which transition represents the line of Balmerseries:
View SolutionA rigorous quantum-mechanical calculation shows that in a hydrogen atom a transition between two sublevels of the fundamental state (see the previous problem) results in the emission or absorption of photons corresponding to a wavelength of 21.1 cm. Experiment is in excellent agreement with this result (to 11 significant figures!).
Making use of classical concepts, try to find the wavelength corresponding to the transition between two sublevels of the ground state of a hydrogen atom, and compare the result with the actual wavelength.
View SolutionThe total energy of an electron in the first excited state of hydrogen atom is about −3.4eV. Its kinetic energy in this state is
View SolutionAs an electron makes a transition from an excited state to the ground state of hydrogen-like atom/ion:
View Solution
