The acceleration due to gravity on a planet of mass 1025 Kg and radius 2580 Km in ms−2 is
1
10
20
100
The correct Answer is:d
g=GMR2=6.67×10−11×1025(2580×103)2
=6.67×10146.66×1012=10+2=100ms−1
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the acceleration due to gravity on a planet is 6.67ms−2 and its radius is 4×106 m, then the mass of the planet is _____ .
A16×1023kgB726×1023kgC16×1024kgD26×1024kgAcceleration due to gravity at earth's surface is 10m−2 The value of acceleration due to gravity at the surface of a planet of mass 12 th and radius 12 of f the earth is -
A5ms−2B10ms−2C20ms−2D40ms−2Acceleration due to gravity at earth's surface is 10ms−2. The value of acceleration due to gravity at the surface of a planet of mass (15)th and radius 12 of the earth is
A4ms−2B6ms−2C8ms−2D12ms−2
The value of acceleration due to gravity at a place is 9.8ms−2. Find its value in kmh−2
View SolutionThe radius and mass of three planets are given below. Arrange them in the decreasing order of acceleration due to gravity. [g=GMR2],g is acceleration due to gravity on a planet, M is mass of the planet and Ris the radius of the planet.
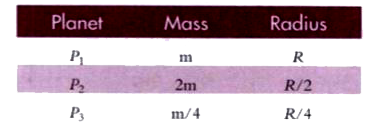
View SolutionIf the acceleration due to gravity on the surface of the earth is 9.8m/s2, what will be the acceleration due to gravity on the surface of a planet whose mass and radius both are two times the corresponding quantities for the earth ?
View SolutionThe acceleration due to gravity at the poles is 10ms−2 and equitorial radius is 6400km for the earth. Then the angular velocity of rotaiton of the earth about its axis so that the weight of a body at the equator reduces to 75% is
View SolutionIf g1 and g2 denote acceleration due to gravity on the surface of the earth and on a planet whose mass and radius is thrice that of earth, then
View Solution
