The acceleration in SHM is always in ……………….. To that of displacement.
opposite phase
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - PROBLEMS FOR PRACTICE
149 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Multiple Choice Question-I
21 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Multiple Choice Question
20 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
A graph between velocity and displacement of a particle performing SHM is shown. Find the acceleration when the particle is at half of maximum displacement from mean position.
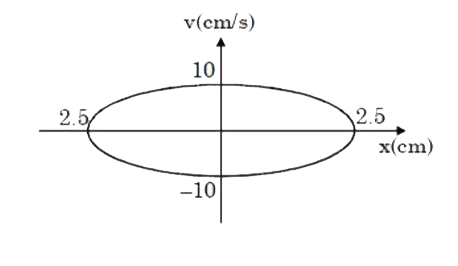
View SolutionShow that in simple harmonic motion (S.H.M.), the acceleration is directly proportional to its displacement at the given instant.
View Solution
Knowledge Check
The acceleration of a body in SHM is
AMaximum at the extreme positionBMaximum at the equilibrium positonCAlways sameDAlways zero.A: In SHM the change in velocity is not uniform.
R: In SHM the acceleration of body varies linearly with its displacement.AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion, then mark (1)BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion, then mark (2)CIf Assertion is true statement but Reason is false then mark (3)DIf both Assertion and Reason are false statements, then mark (4)The acceleration of a particle in S.H.M. is
AAlways zeroBAlways constantCMaximum at the extreme positionDMaximum at the equilibrium position
If a particle executes SHM of time period 4 s and amplitude 2 cm, find its maximum velocity and that at half its full displacement also find the acceleration at the turning points and when the displacement is 0.75 cm
View SolutionThe acceleration of a particle in SHM is 0.8ms−2, when its displacement is 0.2m. The frequency of its oscillation is
View SolutionThe variation of the acceleration (f) of the particle executing S.H.M. with its displacement (X) is represented by the curve
View SolutionSTATEMENT-1 : In simple pendulum performing S.H.M., net acceleration is always between tangential and radial acceleration except at lowest point.
STATEMETN-2 : At lowest point tangential acceleration is zero.
View SolutionA particle is executing SHM. Then the graph of acceleration as a function of displacement is
View Solution
