The adiabatic relation between P and T is
P1−γ.Tγ= constant
PTγ= constant
PγT1−γ= constant
PγTγ−1= constant
The correct Answer is:A
To find the adiabatic relation between pressure (P) and temperature (T), we can follow these steps:
1. Understand the Adiabatic Process:
- An adiabatic process is one in which no heat is exchanged with the surroundings. This means that the change in internal energy is equal to the work done on or by the system.
2. Use the Adiabatic Equation:
- The adiabatic equation is given by:
PVγ=constant
- Here, γ (gamma) is the adiabatic index, defined as:
γ=CpCv
- Where Cp is the molar specific heat at constant pressure and Cv is the molar specific heat at constant volume.
3. Relate Pressure and Volume:
- From the ideal gas law, we know:
PV=nRT
- We can express volume (V) in terms of pressure (P) and temperature (T):
V=nRTP
4. Substitute Volume in the Adiabatic Equation:
- Substitute V in the adiabatic equation:
P(nRTP)γ=constant
- This simplifies to:
P⋅(nRT)γPγ=constant
5. Rearrange the Equation:
- Rearranging gives:
P1−γ(nR)γTγ=constant
- Since nR is a constant, we can denote it as K:
P1−γTγ=K
6. Final Form of the Adiabatic Relation:
- Thus, the adiabatic relation between pressure and temperature can be expressed as:
P1−γTγ=constant
Conclusion:
The adiabatic relation between pressure and temperature is given by:
P1−γTγ=constant
- An adiabatic process is one in which no heat is exchanged with the surroundings. This means that the change in internal energy is equal to the work done on or by the system.
- The adiabatic equation is given by:
PVγ=constant
- Here, γ (gamma) is the adiabatic index, defined as:
γ=CpCv
- Where Cp is the molar specific heat at constant pressure and Cv is the molar specific heat at constant volume.
- From the ideal gas law, we know:
PV=nRT
- We can express volume (V) in terms of pressure (P) and temperature (T):
V=nRTP
- Substitute V in the adiabatic equation:
P(nRTP)γ=constant
- This simplifies to:
P⋅(nRT)γPγ=constant
- Rearranging gives:
P1−γ(nR)γTγ=constant
- Since nR is a constant, we can denote it as K:
P1−γTγ=K
- Thus, the adiabatic relation between pressure and temperature can be expressed as:
P1−γTγ=constant
The adiabatic relation between pressure and temperature is given by:
P1−γTγ=constant
Topper's Solved these Questions
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Problems for practice
54 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Multiple choice questions (NCERT)
10 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - NCERT Questions
10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions
20 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assertion-Reason Type Questions
24 Videos
Similar Questions
Knowledge Check
The relation between Kp and Kx is
AKp=Kx(P∑n)BKp=Kx(P)−ΔnCKp=Kx(P)ΔnDKp=Kx(RT)ΔnFor an adiabatic process the relation between V and T is given by
ATVγ= constantBTγV=constantCTV1−γ= constantDTVγ−1=constantThe relation between T and g is given by
AT∝gBT∝g2CT2∝gDT∝√1g
The relation between T and g is given by
View SolutionThe relation between U,P and V for an ideal gas in an adiabatic process is given by U = 2 + 3 PV. The gas is
View SolutionIn V-T diagram shown in fig., what is the relation between P1andP2 ?
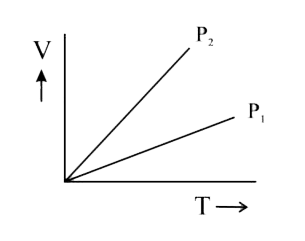
View SolutionIn the following V - T diagram what is the relations between P1andP2 :

View SolutionThe relation between U, p and V for an ideal gas in an adiabatic process is given by relation U=a+bpV. Find the value of adiabatic exponent (γ) of this gas.
View Solution
