The air in a closed tube 34cm long is vibrating with two nodes and two antinodes and its temprature is 51∘C. What is the wavelength of the waves produced in air outside the tube, when the temperature of air is 16∘C?
42.8cm
68cm
17cm
102cm
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the setup
We have a closed tube of length L=34cm that has two nodes and two antinodes. In a closed tube, the relationship between the length of the tube and the wavelength of the sound wave can be expressed as:
L=nλ4
where n is the number of quarter wavelengths fitting into the tube.
Step 2: Determine the number of wavelengths
In this case, since there are two nodes and two antinodes, we can say that n=3 (as there are three quarter wavelengths in the tube). Therefore, we can write:
L=3λ4
Step 3: Solve for the wavelength at 51°C
Rearranging the equation to solve for λ:
λ=4L3
Substituting the value of L:
λ=4×34cm3=136cm3≈45.33cm
Step 4: Convert temperatures to Kelvin
Next, we need to convert the temperatures from Celsius to Kelvin:
- For T=51°C:
T=51+273=324K
- For T′=16°C:
T′=16+273=289K
Step 5: Use the relationship between wavelength and temperature
The speed of sound in air is related to temperature, and we can express the relationship between the wavelengths at different temperatures using:
λ′λ=√T′T
where λ′ is the wavelength at T′ and λ is the wavelength at T.
Step 6: Substitute the known values
Substituting the known values into the equation:
λ′45.33=√289324
Step 7: Calculate λ′
Now, we calculate √289324:
√289324=1718
Thus,
λ′=45.33×1718≈42.8cm
Final Answer
The wavelength of the waves produced in air outside the tube at 16°C is approximately 42.8cm.
---
We have a closed tube of length L=34cm that has two nodes and two antinodes. In a closed tube, the relationship between the length of the tube and the wavelength of the sound wave can be expressed as:
L=nλ4
where n is the number of quarter wavelengths fitting into the tube.
In this case, since there are two nodes and two antinodes, we can say that n=3 (as there are three quarter wavelengths in the tube). Therefore, we can write:
L=3λ4
Rearranging the equation to solve for λ:
λ=4L3
Substituting the value of L:
λ=4×34cm3=136cm3≈45.33cm
Next, we need to convert the temperatures from Celsius to Kelvin:
- For T=51°C:
T=51+273=324K
- For T′=16°C:
T′=16+273=289K
The speed of sound in air is related to temperature, and we can express the relationship between the wavelengths at different temperatures using:
λ′λ=√T′T
where λ′ is the wavelength at T′ and λ is the wavelength at T.
Substituting the known values into the equation:
λ′45.33=√289324
Now, we calculate √289324:
√289324=1718
Thus,
λ′=45.33×1718≈42.8cm
The wavelength of the waves produced in air outside the tube at 16°C is approximately 42.8cm.
Topper's Solved these Questions
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Single correct option
1 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Level 2 More Than One Correct
5 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Subjective Questions
1 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
Similar Questions
At what temperatures (in∘C) will the speed of sound in air be 3 times its value at O∘C?
View SolutionAt the middle of the mercury barometer tube there is a little column of air with the length l0 and there is vacuum at the top as shown. Under the normal atmospheric pressure and the temperature of 200 le,vom/ l0=10cm. What will be the length of the air column if the temperature rises to 330 kelvin? (Neglict expansion of the tube)
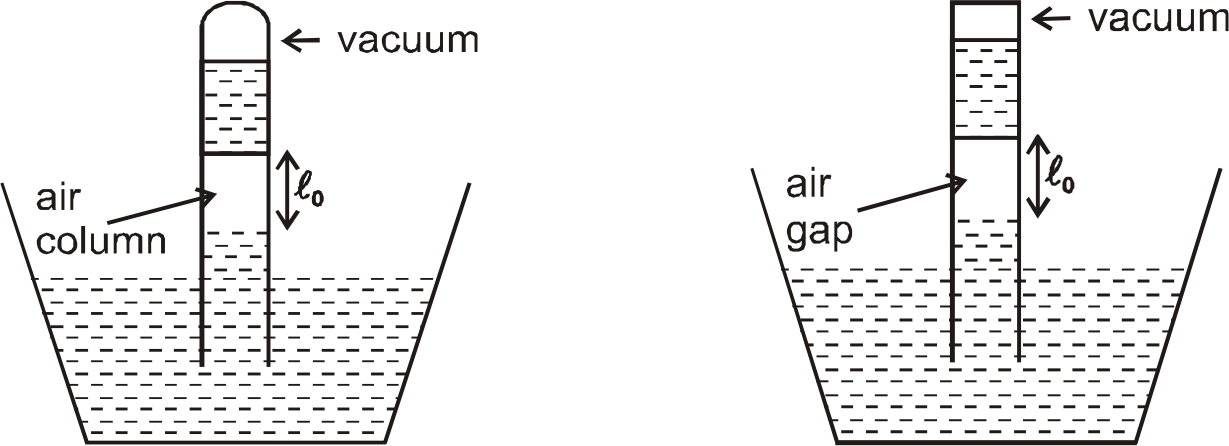
View Solution
Knowledge Check
A tuning fork vibrating with a frequency of 500 Hz is kept close to the open end of a tube filled with water, as shown in figure. The water level in the tube is gradually lowered When the water level is 17 cm below the open to open end, maximum intensity of sound is heard. If the room temperature is 20∘ C, the speed of sound in air at the temperature is
 A1. 330ms−1B2. 340ms−1C3. 350ms−1D4. 360ms−1
A1. 330ms−1B2. 340ms−1C3. 350ms−1D4. 360ms−1
Air is pumped into an automobile tyre's tube up to pressure pf 200kPa in the morning when the air temperature is 20∘C.During the day the temperature rises to 40∘C and the tube expand by 2%. Calculate the pressure of the air in the tube at this temperature.
View SolutionA column of air at 51∘C and a tuning fork produce 4 beats per second when sounded together. As the temperature of the air column is decreased, the number of beats per second tends to decrease and when the temperature is 16∘C the two produce 1 beat per second. Find the frequency of the tuning fork.
View SolutionA column of air at 51∘C and a tuning fork produce 4 beats per second when sounded together. As the temperature of the air column is decreased, the number of beats per second tends to decrease and when the temperature is 16∘C the two produce 1 beat per second. Find the frequency of the tuning fork.
View SolutionA tuning fork produces a wave of wavelength 110 cm in air at O0C. The wavelength at 25∘C would be
View SolutionA glass tube sealed at both ends is 100cm long, It lies horizontally with the middle 10cm containing mercury. The two ends of the tube contain air at 27∘Cand at a pressure 76cm of mercury. The air column on one side is maintained at 0∘Cand the other side is maintained at 127∘C. Calculate the length of the air column on the cooler side. neglect the changes in the volume of mercury and of the glass.
View SolutionIn a standing wave pattern in a vibrating air column, nodes are formed at a distance of 4.0 cm. If the speed of sound in air is328ms−1 what is the frequency of the source ?
View SolutionA closed air column 32cm long is in resonance with a tuning fork . Another open air column of length 66cm is in resonance with another tuning fork . If the two forks produce 8beats/s when sounded together , find
the speed of sound in the air
View Solution
