The amplitude of vibration of a particle is given by am=(a0)/(aω2−bω+c), where a0, a, b and c are positive. The condition for a single resonant frequency is
b2=4ac
b2>4ac
b2=5ac
b2=7ac
The correct Answer is:A
aω2−bω+c=0⇒ω=b±√b2−4ac2a
For single frequency b2=4ac
Topper's Solved these Questions
Similar Questions
The velocity of the particle of mass m as a function of time t is given by v=Aω.cos[√Kmt] , where A is amplitude of oscillation. The dimension of AK is
View SolutionA particle of mass m moves under the action of a central force. The potential energy function is given by U(r)=mkr3 Where k is a positive constant and r is distance of the particle from the centre of attraction. (a) What should be the kinetic energy of the particle so that it moves in a circle of radius a0 about the centre of attraction? (b) What is the period of this circualr motion ?
View Solution
Knowledge Check
- Question 1 - Select One
The amplitude of velocity of a particle is given by, Vm=V0/(aω2−bω+c) where V0, a, b and c are positive :
The condition for a single resonant frequency isAb2<4acBb2=4acCb2=5acDb2=7ac - Question 2 - Select One
The displacement of particle is given by
x=a0+a1t2−a2t23
What is its acceleration ?A2a23B−2a23Ca2DZero - Question 3 - Select One
The displacement of particle is given by
x=a0+a1t2−a2t23
What is its acceleration ?A2a23B−2a23Ca2DZero
The wave function of 2s electron is given by
W2s=14√2π(1a0)3/2(2−ra0)e−1a0
It has a node at r=rp .Find the radiation between rp and aView SolutionThe period of oscillation of a particle in SHM is 4sec and its amplitude of vibration is 4cm. The distance of the particle 0.5s after passsing the mean position is
View SolutionThe first obrital of H or H like atom is represencted by
ψ=1√π(Za0)3/2e−ze/a0
where a0= Bohr's orbit . The actual probability of fiding the elercrton at a distance r form the nucleus is :View SolutionThe cubical container ABCDEFGH which is completely filled with an ideal (nonviscous and incompressible) fluid, moves in a gravity free space with a acceleration of a=a0(ˆi−ˆj+ˆk) where a0 is a positive constant. Then the minimum pressure at the point will be
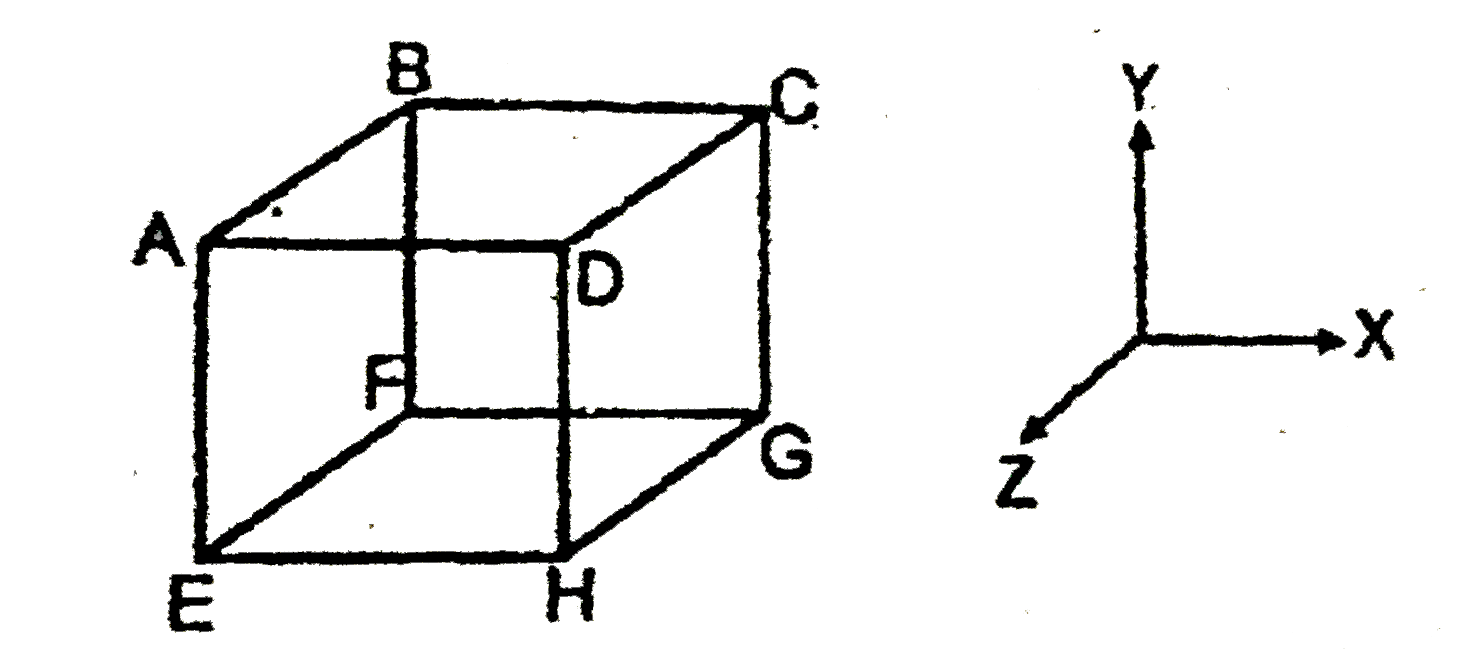 View Solution
View SolutionOn the superposition of the two waves given as y1=A0sin(ωt−kx) and y2=A0cos(ωt−kx+π6) , the resultant amplitude of oscillations will be
View Solution

