The answer to each of the following questions is a single-digit integer ranging from 0 to 9. Darken the correct digit.
Two identical air capacitors are connected in series to a battery. Let Q be the charge supplied by the battery in this case. Now the space between the plates of one of the capacitors is filled with a dielectric slab of dielectric constant 3, while the battery remains connected. Let ΔQ be the additional charge supplied by the battery after the insertion of slab. Calcualate QΔQ.
The correct Answer is:2
To solve the problem, we need to calculate the ratio QΔQ where Q is the charge supplied by the battery when two identical air capacitors are connected in series, and ΔQ is the additional charge supplied after inserting a dielectric slab in one of the capacitors.
1. Identify the capacitance of the capacitors:
Let the capacitance of each air capacitor be C.
2. Calculate the equivalent capacitance of two capacitors in series:
For two capacitors in series, the equivalent capacitance Ceq is given by:
1Ceq=1C+1C=2C
Therefore,
Ceq=C2
3. Calculate the charge Q supplied by the battery:
The charge Q supplied by the battery is given by:
Q=Ceq⋅V=C2⋅V
4. Introduce the dielectric slab:
When a dielectric slab with a dielectric constant K=3 is inserted into one of the capacitors, the capacitance of that capacitor becomes:
C′1=K⋅C=3C
The other capacitor remains unchanged:
C2=C
5. Calculate the new equivalent capacitance C′eq:
The new equivalent capacitance with the dielectric slab is:
1C′eq=1C′1+1C2=13C+1C
Finding a common denominator:
1C′eq=13C+33C=43C
Thus,
C′eq=3C4
6. Calculate the new charge Q′ supplied by the battery:
The new charge Q′ supplied by the battery after the dielectric is inserted is:
Q′=C′eq⋅V=3C4⋅V
7. Calculate the additional charge ΔQ:
The additional charge ΔQ is given by:
ΔQ=Q′−Q=(3C4⋅V)−(C2⋅V)
To simplify:
ΔQ=3CV4−2CV4=CV4
8. Calculate the ratio QΔQ:
Now we can find the ratio:
QΔQ=CV2CV4=CV2⋅4CV=2
Final Answer:
QΔQ=2
Let the capacitance of each air capacitor be C.
For two capacitors in series, the equivalent capacitance Ceq is given by:
1Ceq=1C+1C=2C
Therefore,
Ceq=C2
The charge Q supplied by the battery is given by:
Q=Ceq⋅V=C2⋅V
When a dielectric slab with a dielectric constant K=3 is inserted into one of the capacitors, the capacitance of that capacitor becomes:
C′1=K⋅C=3C
The other capacitor remains unchanged:
C2=C
The new equivalent capacitance with the dielectric slab is:
1C′eq=1C′1+1C2=13C+1C
Finding a common denominator:
1C′eq=13C+33C=43C
Thus,
C′eq=3C4
The new charge Q′ supplied by the battery after the dielectric is inserted is:
Q′=C′eq⋅V=3C4⋅V
The additional charge ΔQ is given by:
ΔQ=Q′−Q=(3C4⋅V)−(C2⋅V)
To simplify:
ΔQ=3CV4−2CV4=CV4
Now we can find the ratio:
QΔQ=CV2CV4=CV2⋅4CV=2
QΔQ=2
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Competition file (NCERT Exemplar Problems: Multiple Choice Questions Type-I)
6 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Competition file (NCERT Exemplar Problems: Multiple Choice Questions Type-II)
7 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Competition file (MATRIX TYPE QUESTIONS)
1 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
The answer to each of the following questions is a single-digit integer ranging from 0 to 9. Darken the correct digit.
A metal plate with total charge Q on it, is placed parallel to a dielectric slab of same area. Let q be the charge appearing on the surface of dielectric whose dielectric constant is 2. Calculate Q/q.
View SolutionA capacitor of some capacitance is charged by a 12V battery.Now the space between the plates of capacitors is filled with a dielectric of dielectric constant K=0.5 and again it is charged. The magnitude of the charge will
View Solution
Knowledge Check
The terminals of a battery of emf V are connected to the two plates of a parallel plate capacitor. If the space between the plates of the capacitor is filled with an insulator of dielectric constant K, then :
Athe electric field in the space between the plates does not changeBthe capacitance of the capacitor increasesCthe charge stored in the capacitor increasesDthe electrostatic energy stored in the capacitor decreasesSpace between the plates of a parallel plate capacitor is filled with a dielectric slab. The capacitor is charged and then the supply is disconnected to it. If the slab is now taken out then
Awork is not done to take out the slabBenergy stored in the capacitor reducesCpotential difference across the capacitor is decreasedDpotential difference across the capacitor is increasedHalf of the space between the plates of a parallel plate capacitor is filled with a dielectric material of dielectric constant K . The ramaining half contains air as shown in the figure . The capacitor is now given a charge Q . Then
 Aelectric field in the dielectric filled region is higher than that in the air - filled region.Bon the two halves of the bottom plate the charge densities are unequal.Ccharge on the half of the top plate above the air filled part is QK+1.Dcapacitance of the capacitor shown above is (1+K)C02, where C0 is the capacitance of the same capacitor with dielectric removed.
Aelectric field in the dielectric filled region is higher than that in the air - filled region.Bon the two halves of the bottom plate the charge densities are unequal.Ccharge on the half of the top plate above the air filled part is QK+1.Dcapacitance of the capacitor shown above is (1+K)C02, where C0 is the capacitance of the same capacitor with dielectric removed.
Two identical parallel plate capacitors A and B are connected to a battery of V volts with the switch S closed . The switch is now opened and the free space between the plates of the capacitors is filled with dielectric of dielectric constant K . Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric .
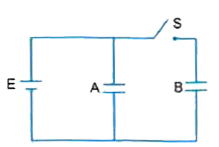
View SolutionThe answer to each of the following questions is a single-digit integer ranging from 0 to 9. Darken the correct digit.
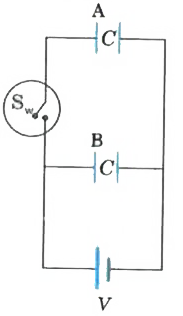
Two identical air capacitors of capacitance C are connected to a battery of EMF V and initially switch is closed for a long time. After the switch is opened, identical dielectric slabs are inserted in between the plates of both the capacitors and it is found that energy stored in capacitor B becomes nine times of the energy stored in capacitor A. What is the dielectric constant of the slab?
View SolutionThe figure shows two identical parallel plate capacitors connected to a battery with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant(or relative permittivity) 3. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.

View SolutionA parallel plate capacitor is charged completely and then disconnected from the battery. IF the separation between the plates is reduced by 50% and the space between the plates if filled with a dielectric slab of dielectric constant 10, then the potential difference between the plates
View SolutionTwo identical capacitor C1 and C2 are connected in series with a battery. They are fully charged. Now a dielectric slab is inserted between the plates of C2. The potential across C1 will :

View Solution
