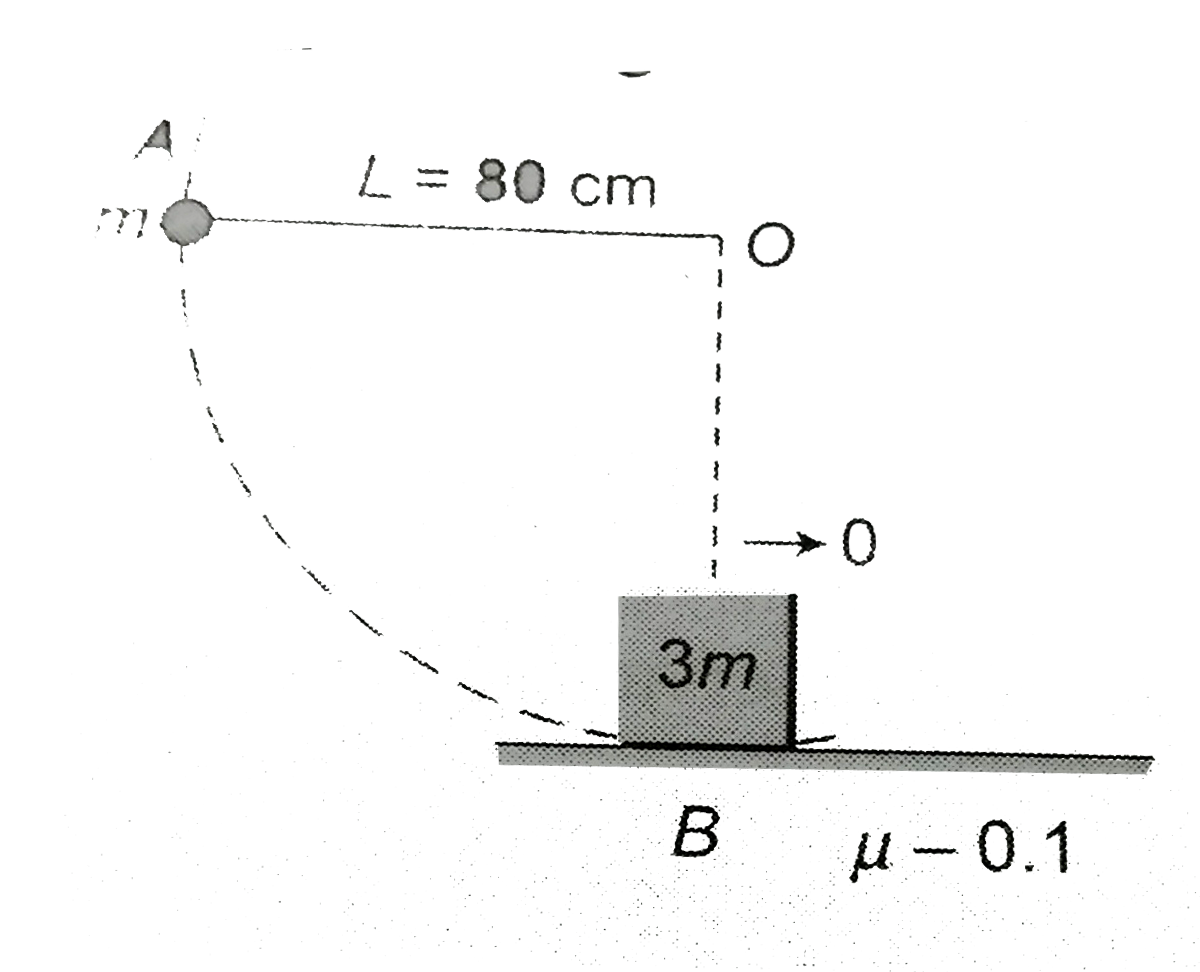
The ball A of mass m is released when the string is horizontal. It strikes a block B of mass 3m kept on a rough surface of friction coefficient μ=0.1. If a head on elastic collision takes place , find the maximum distance travelled by the block on a rough surface.
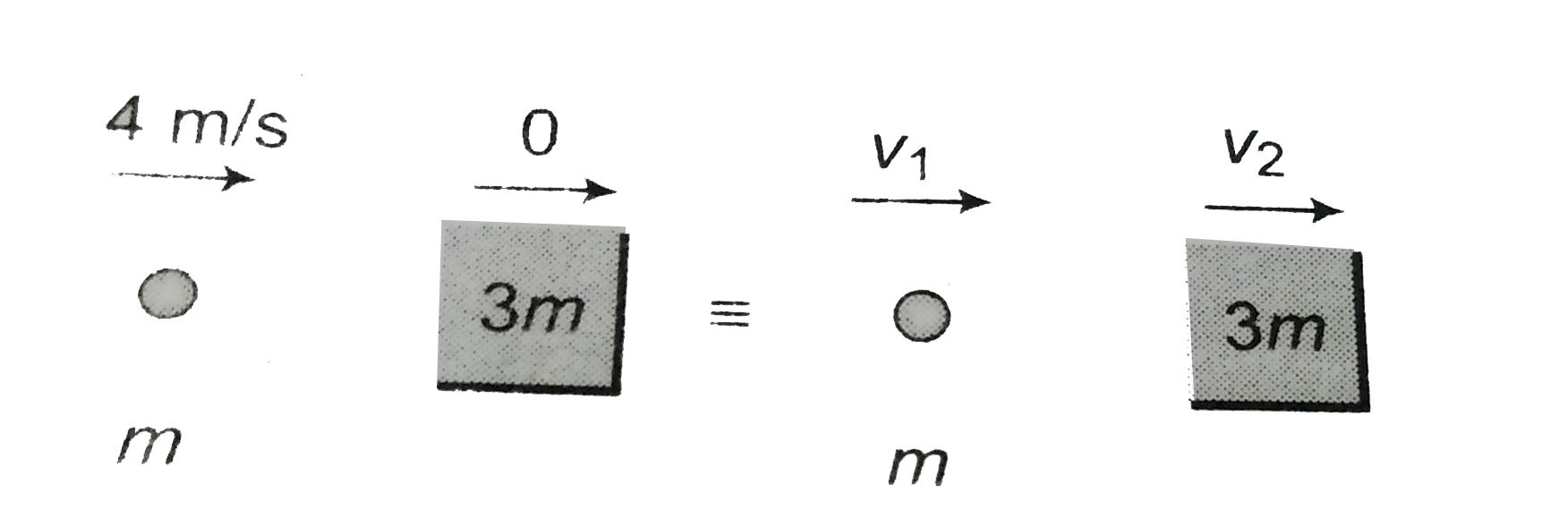
when the ball reaches at the bottom , its velocity
u=√2gL=√2×10×0.8=4m/s
Now the head - on elastic collision between the ball and the block
m×4+3m×0=mv1+3mv2 (i)
v1+4=v2+0 (ii)
Solving , v2=2m/s
Now , the block moves on a rough surface
Due to the friction the block will stop after travelling a distance d.
Retardation of block is
a=3μmg3m=μg=0.1×10=1m/s2
0=(2)2−2ad⇒0=4−2×1×d⇒d=2m

Topper's Solved these Questions
Similar Questions
Knowledge Check
In the previous problem , if the horizontal surface is rough with friction coefficient 0.5 and collision is elastic , head - on , the distance travelled by the block on the rough surface
A5mB10mC15mD20mA block of mass m lying on a rough horizontal surface of friction coefficient μ is pulled by a force F as shown , the limiting friction between the block and surface will be
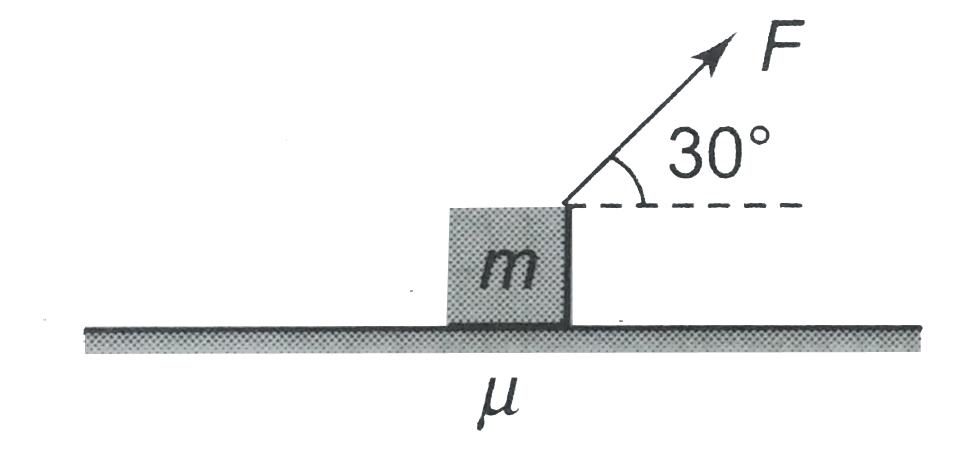 AμmgBμ(mg+F2)Cμ(mg−F2)Dμ(mg−√3F2)
AμmgBμ(mg+F2)Cμ(mg−F2)Dμ(mg−√3F2)A block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
AmgBmg sin θCμmgcosθDμmgsinθ
A body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
View SolutionA block of mass m=1/3 kg is kept on a rough horizontal plane. Friction coefficient is μ=0.75. The work done by minimum force required to drag to the block along the plane by a distance 5m is :-
View SolutionA block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass m is pulled by a constant powert P placed on a rough horizontal plane. The friction coefficient the block and surface is μ. The maximum velocity of the block is.
View Solution