The bottom of glass beaker is made of a thin equiconvex lens having bottom side silver polished as shown in figure,. Now the water is filled in the baker upto a height of h=4m. The image of point object floating at middle point of beaker at the surface of water coincides with it. Find out the value of radius of curvature of lens. (.aμg=3/2,.aμw=4/3)

The correct Answer is:5m
Power of equivalent mirror,P′M=2P2+PM
1f2=(3/24/2−1)(1R+1R)=18×2R=14R
f2=4R and P2=14R
−1f′m=2×14R+2R=52R
f′m=−25R
|h|=2|f′m|
h=2×25R=4m
R=5m
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Single Correct221videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.721videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
Bottom of a glass beaker is made of a thin equi-convex lens having bottom side silver polished as shown in the figure. Water is filled in the beaker upto a height 4m. The image of poin to bject,floating at middle point of beaker at the surface of water coincides with it. Find out ther adius of curvature of the lens.Given that refractive index of glass is 3/2 and that of water is 4/3.
 View Solution
View SolutionConsider the situation shown in figure. Water (μw=43) is filled in a breaker upto a height of 10 cm. A plane mirror is fixed at a height of 5 cm from the surface of water. Distance of image from the mirror after reflection from it if an object O at the bottom of the beaker is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of refractive index of water to be 4/3.
A2.6m2B3.6m2C4.2m2D5.8m2
A thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its priincipal axis, the object coincides with its own image.

Q. The radius of curvature of the convex surface isView SolutionA vessel having perfectly reflecting plane botton is filled with water (μ=4/3) to depth d. A point source of light is placed at a height h above the surface of water. Find the distance of final image from water surface.
View SolutionA transparent solid sphere of radius 2cm and density ρ floats in a transparent liquid of density 2ρ kept in a beaker. The bottom of the beaker is spherical in shape with radius of curvature 8cm and is silvered to make it concave mirror as shown in the figure. When an object is placed at a distance of 10cm directly above the centre of the sphere C, its final image coincides with it. Find h (as shown in the figure ), the height of the liquid surface in the beaker from the apex of the bottom. Consider the paraxial rays only. The refractive index of the sphere is 3/2 and that of the liquid is 4/3.
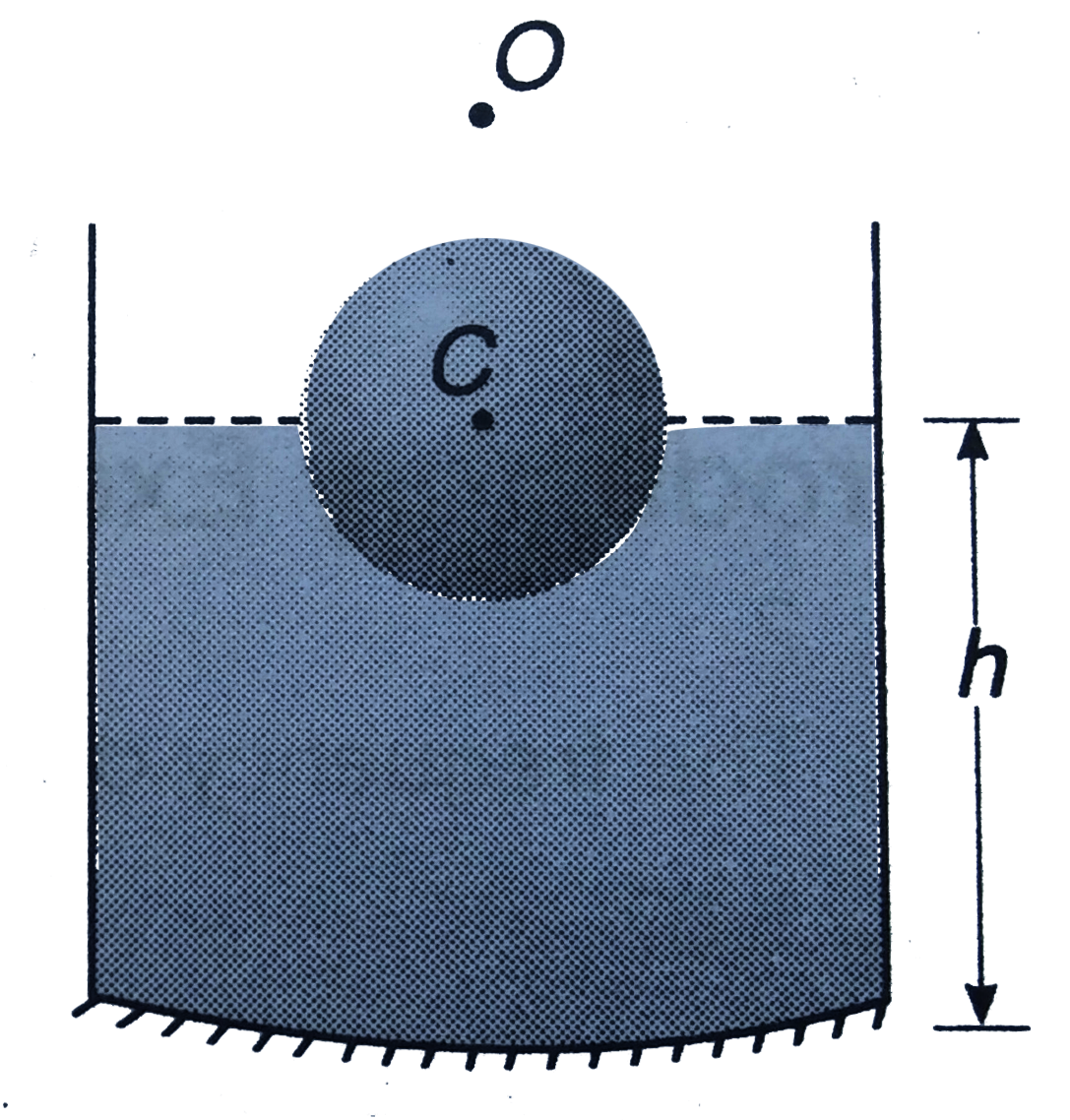 View Solution
View SolutionA thin equiconvex glass lens (μ1=1.5) of radius of curvature 'R' and a thin plano-concave lens (μ2=1.4) are kept in contact and the plane surface is silvered. This lens system is placed in air. When a point object is placed at a distance 20cm from the lens system on its principal axis, the image formed by the lens system coincides with the object. Then the value of radius of curvature 'R' is
 View Solution
View SolutionThe lower end of a clean glass capillary tube of internal radius 2×10−4m is dippled into a beaker containing water . The water rise up the tube to a vertical height of 7×10−2m above its level in the beaker. Calculate the surface tension of water. Density of water = 1000kgm−3,g=10ms−2 .
View SolutionTwo thin similar convex glass are joined together front to front, with its rear portion silvered such that a sharp image is formed 0.2m for an object at infinity. When the air between the glass pieces is replaced by water (μ=43), find the position of image.
View SolutionA small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of refractive index of water to be 4/3.
View Solution
