The breaking force of wire is 104N and radius is 1×10−3m. If the radius is 2×10−3m, then the breaking force will be
4×104N
40×104N
0.04×104N
0.4×104N
The correct Answer is:A
F2F1=(r2r1)2=(2×10−31×10−3)2=4
F2=4F1
=4×104N.
Topper's Solved these Questions
Similar Questions
A wire of length 1m is stretched by a force of 10N. The area of cross-section of the wire is 2×10–6m2 and Y is 2×1011N/m2 . Increase in length of the wire will be -
View SolutionThe breaking stress of the material of a wire is 6×106Nm−2 Then density ρ of the material is 3×103kgm−3. If the wire is to break under its own weight, the length (in metre) of the wire made of that material should be (take g=10ms−2)
View Solution
Knowledge Check
- Question 1 - Select One
The mass of the moon is 7.34×1022kg and the radius is 1.74×106m. The value of gravitation force will be
A1.45N/kgB1.55N/kgC1.75N/kgD1.62N/kg - Question 2 - Select One
If a uniform brass wire of length 5 m and radius 10−3 m is extended by 10−3m, then the energy stored in the wire will be
(Young's modulus for brass =10×1010N/m2)A3.14×10−2JB3.14×10−1JC2×10−3JD3.14×10−4J - Question 3 - Select One
The breaking stress of a wire is 7.2×108N/m2 and density is 78×102kg/m3. The wire is held vertically to the rigid support. The maximum length so that the wire does not break is
A9.94×103mB9.4×103mC94×103mD940×103m
A particular force (F) applied on a wire increases its length by 2×10−3 m. To increases the wire's length by 4×10−3 m, the applied force will be
View SolutionTwo blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2×109N m−2. If g=10ms−2, then what is the minimum radius of the wire which will not break
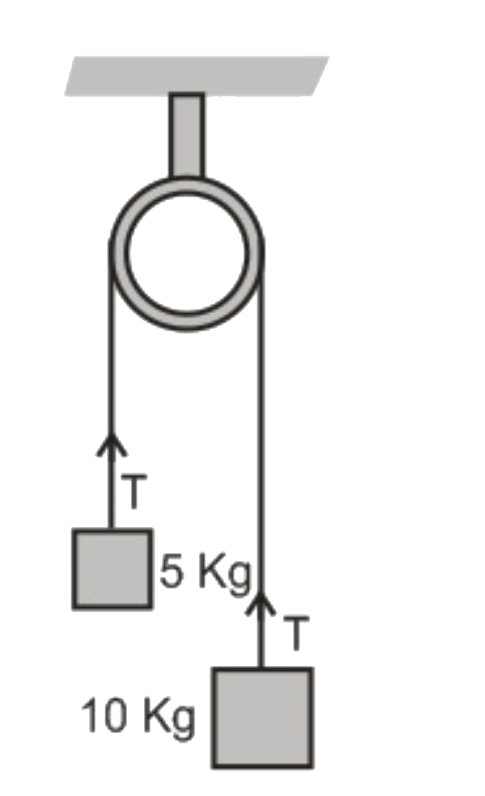 View Solution
View SolutionA wire of area of cross section 1×10−6m2 and length 2 m is stretched through 0.1×10−3m. If the Young's modulus of a wire is 2×1011N/m2, then the work done to stretch the wire will be
View SolutionA copper wire of length 4.0mm and area of cross-section 1.2cm2 is stretched with a force of 4.8×103N. If Young's modulus for copper is 1.2×1011N/m2, the increases in the length of the wire will be
View SolutionFor steel the breaking stressis 6×106N/m2 and the density is 8×103kg/m3. The maximum length of steel wire, which can be suspended witout breaking under its own weight is [g=10m/s2]
View Solution

