The breaking stress of a wire depends on
 length of the wire
radius of the wire
material of the wire
shape of the cross-section
The correct Answer is:C
The breaking stress of the wire depends upon the nature of the material of the wire.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Hooke'S Law
3 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Stress-Strain Curve
5 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Elastic Behavior Of Solids
2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
The breaking stress is
Athe stress just below the elastic limitBthe stress just above the elastic limitCthe greatest stress that the material can bearDthe stress for which the residual strain is 0.0002The breaking stress of a wire of length L and radius r is 5kg−wt/m2. The wire of length 2l and radius 2r of the same material will have breaking stress in kg−wt/m2
A5B10C20D80The breaking stress of a wire is 7.2×108N/m2 and density is 78×102kg/m3. The wire is held vertically to the rigid support. The maximum length so that the wire does not break is
A9.94×103mB9.4×103mC94×103mD940×103m
The breaking stress for a wire of radius r of given material is F N/m2. The breaking stress for the wire of same material of radius 2r is:
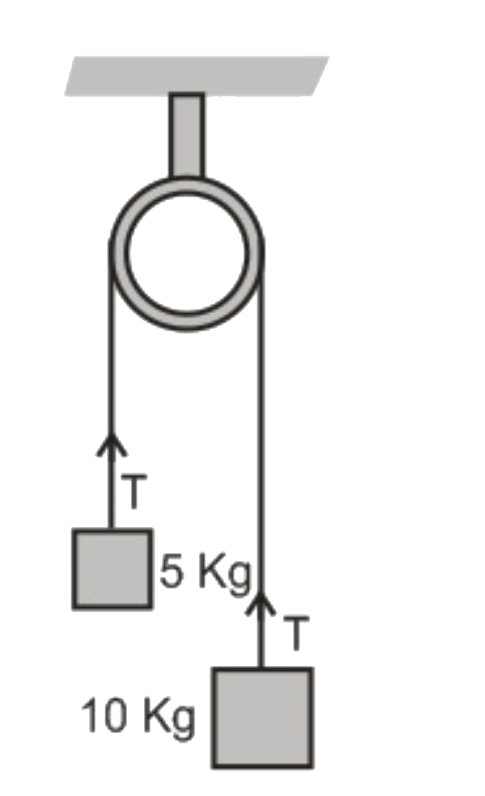
View SolutionTwo blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2×109N m−2. If g=10ms−2, then what is the minimum radius of the wire which will not break
View SolutionBreaking stress does not depend upon
View SolutionIf breaking stress of a wire of length L and radius of cross-section r is P N/m2, then breaking stress of wire of same material of length 2 L and radius of cross section (r/2) will be
View SolutionThe resistivity of a wire depends on its
View Solution
