The breaking stress of a wire depends on
material of the wire
length of the wire
radus of the wire
shape of the cross section
Step by step video & image solution for The breaking stress of a wire depends on by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective 2
7 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Short Answer
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- SOUND WAVESBOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - Exercises
89 Videos
Similar Questions
Knowledge Check
The breaking stress is
Athe stress just below the elastic limitBthe stress just above the elastic limitCthe greatest stress that the material can bearDthe stress for which the residual strain is 0.0002The breaking stress of a wire of length L and radius r is 5kg−wt/m2. The wire of length 2l and radius 2r of the same material will have breaking stress in kg−wt/m2
A5B10C20D80The breaking stress of a wire is 7.2×108N/m2 and density is 78×102kg/m3. The wire is held vertically to the rigid support. The maximum length so that the wire does not break is
A9.94×103mB9.4×103mC94×103mD940×103m
The breaking stress for a wire of radius r of given material is F N/m2. The breaking stress for the wire of same material of radius 2r is:
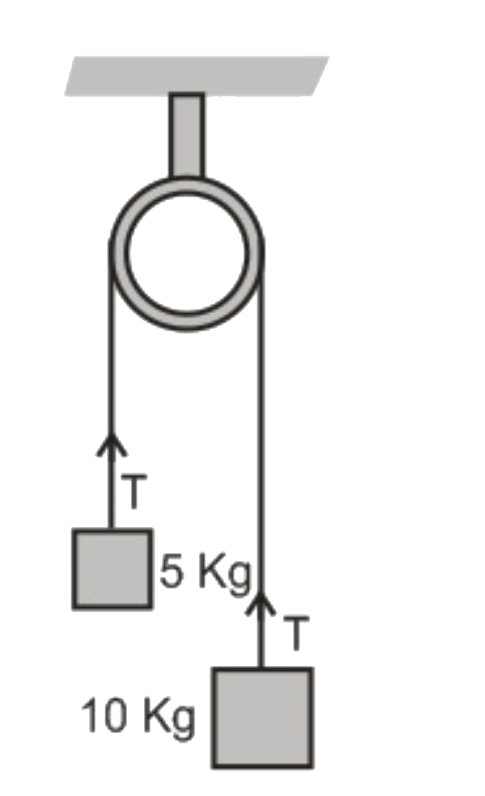
View SolutionTwo blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2×109N m−2. If g=10ms−2, then what is the minimum radius of the wire which will not break
View SolutionBreaking stress does not depend upon
View SolutionIf breaking stress of a wire of length L and radius of cross-section r is P N/m2, then breaking stress of wire of same material of length 2 L and radius of cross section (r/2) will be
View SolutionThe resistivity of a wire depends on its
View Solution
