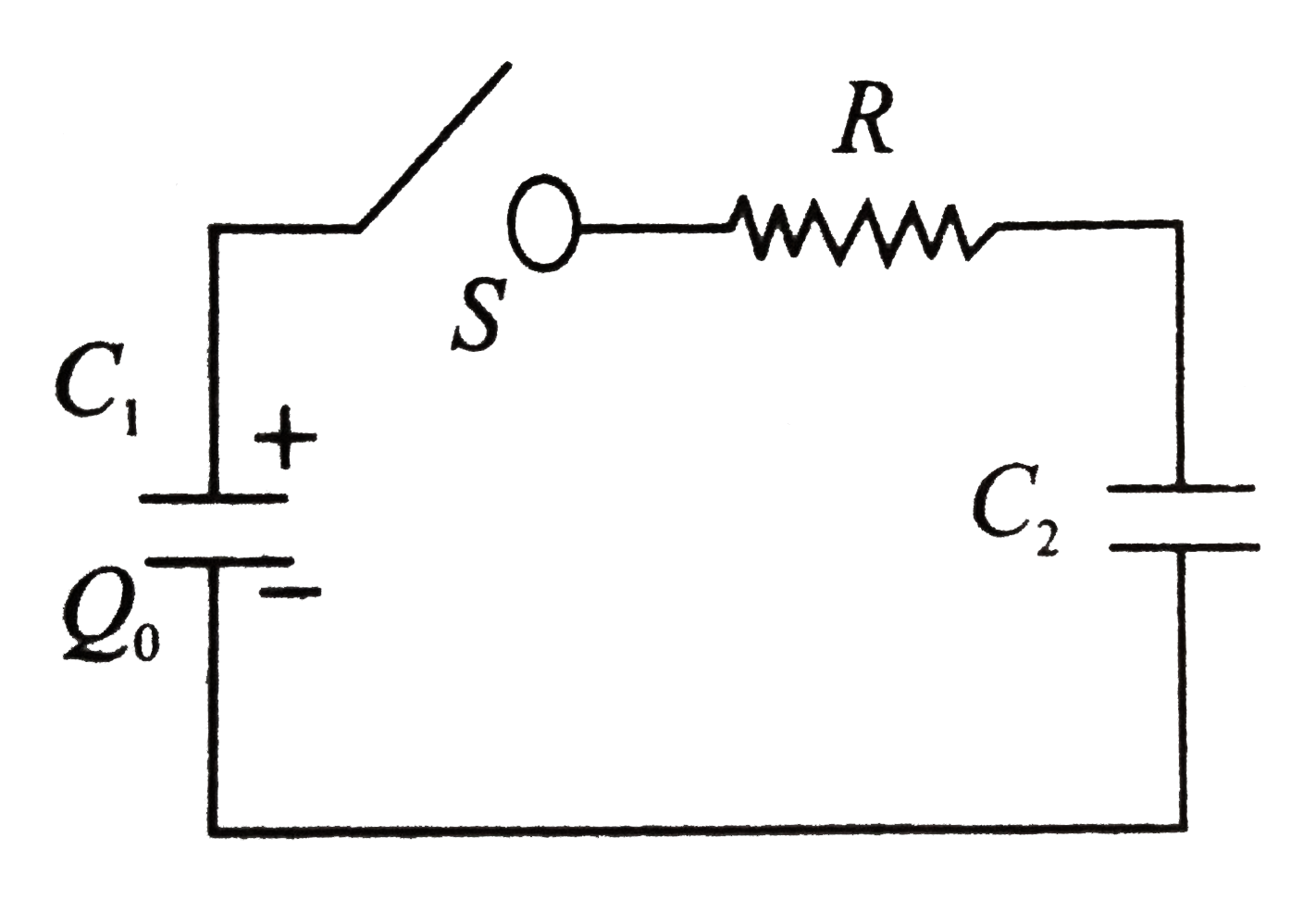
The capacitor C1 in the figure shown initially carries a charge q0. When the switches S1 and S2 are closed, capacitor C1 is connected in series to a resistor R and a second capacitor C2 which is initially uncharged.

The charge flown through wires as a function of time is
where C=C1C2C1+C2
q0e−tRC+CC2q0
q0CC1x[1−e−tRC]
q0CC1e−tCR
q0e−tRC
The correct Answer is:B
Finally the capacitors are in parallel and total charge (=q0) distributes between them in direct ratio of capacity.
∴qC2=(C2C1+C2)q0→ in steady state .
but this chasrge increases exponentially.
Hence, charge on C2 at any time t is
qC2=(C2q0C1+C2)(1−e−tτC)
Initially C2 is uncharged so, what ever is the charge on C2 it is charge flown through switches.
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- CAPACITORSBOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
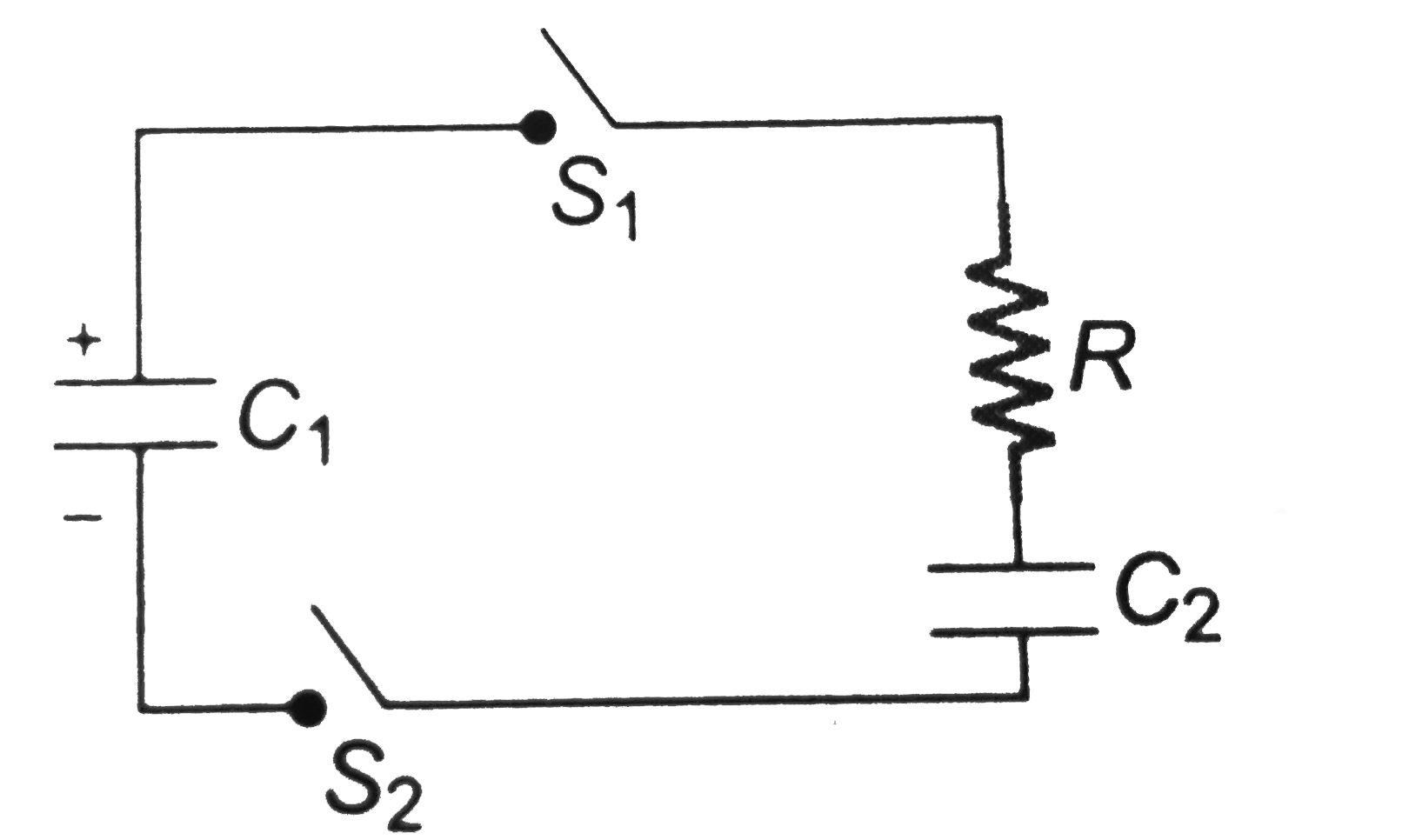
The capacitor C1 in the figure initially carries a charge q0. When the switch S1 and S2 are shut, capacitor C1 is connected in series to a resistor R and a second capacitor C2, which initially does not carry any charge.
If the heat lost in the resistor after a long time of closing the switch is q20C2kC1(C1+C2), then Find the value of k.
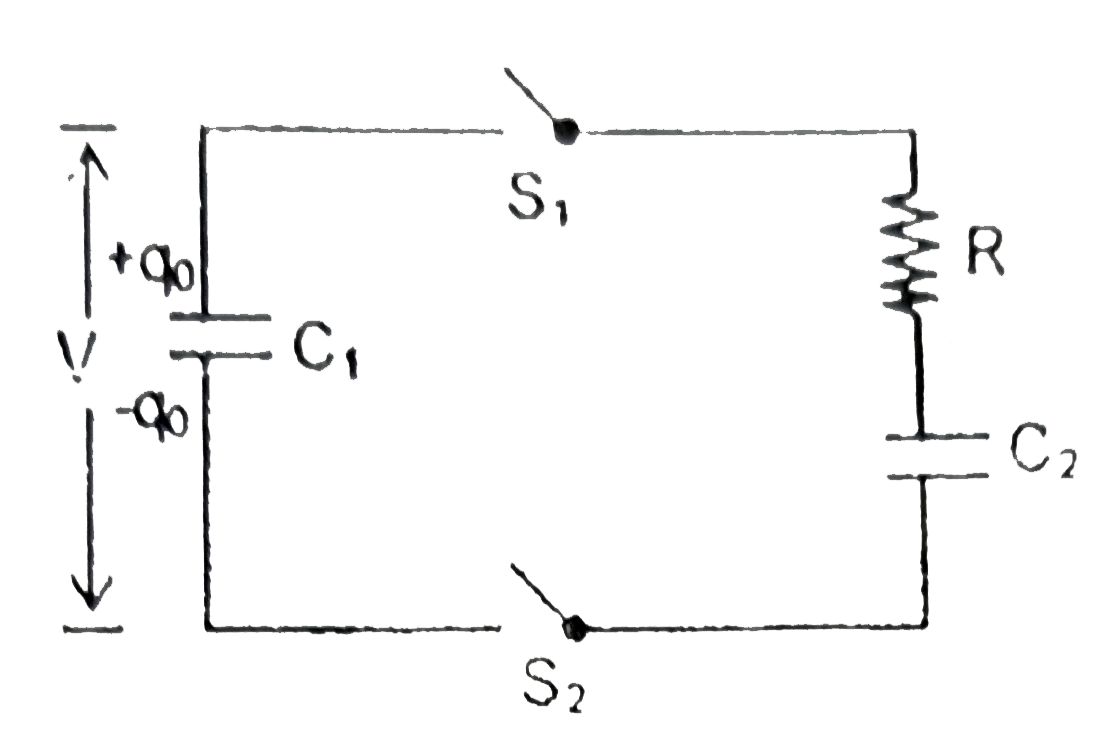
View SolutionThe capactor C1 in the figure initially carries a charge q0. When the i switch S1 and S2 are closed, capacitor C1 is connected to a resistor R and a second capacitor C2, which initially does not carry any charge.
(a) Find the charges deposited on the capacitors in steady state and the current through R as a function of time.
(b) What is heat lost in the resistor after a long time of closing the switch?
View Solution
Knowledge Check
The capacitor C1 in the figure shown initially carries a charge q0. When the switches S1 and S2 are closed, capacitor C1 is connected in series to a resistor R and a second capacitor C2 which is initially uncharged.
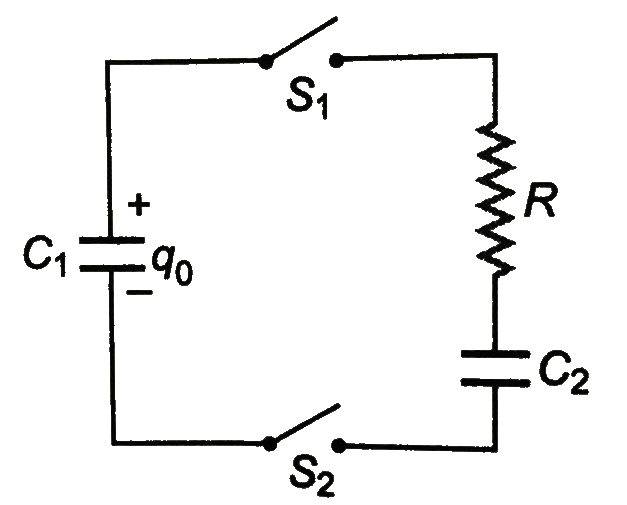
the total head dissipated in the circuit during the discharging process of C1 isAq202C21×CBq202CCq20C22C21Dq202C1C2In the circuit shown initially C1,C2are uncharged. After closing the switch
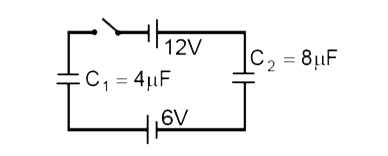 AThe charge on C2 is greater that on C1BThe charge on C1 and C2 are the sameCThe potential drops across C1 and C2 are the sameDThe potential drops across C2 is greater than that across C1
AThe charge on C2 is greater that on C1BThe charge on C1 and C2 are the sameCThe potential drops across C1 and C2 are the sameDThe potential drops across C2 is greater than that across C1In the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
 Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R)
Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R)
In the following circuit, the switch S is closed at t = 0. The charge on the capacitor C1 as a function of time will be given by (Ceq=C1C2C1+C2)

View SolutionThe capacitor shown in figure has been charged to a potential difference of V volt, so that it carries a charge CV with both the switches S1andS2 remaining open. Switch S1 is closed at t=0. At t=R1C switch S1 is opened and S2 is closed. Find the charge on the capacitor at t=2R1C+R2C.

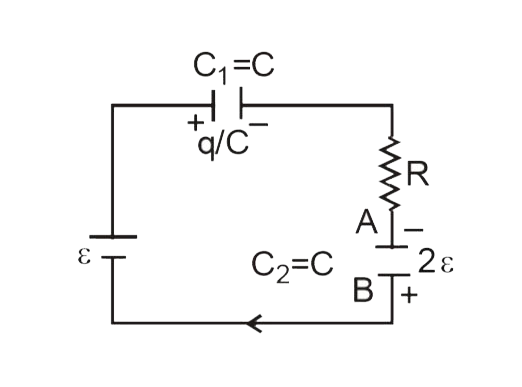
View SolutionIn the figure shown below, find out the current as function of time and charge on capacitor C1and also plot the graph of charge on plate A and B of capacitor C2 as a function of time.
View SolutionIn the given figure switch is open initially and capacitor C2 is unchanged
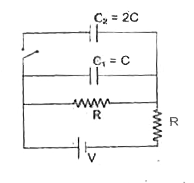
Energy in C1 is
View SolutionIn the given figure switch is open initially and capacitor C2 is unchanged
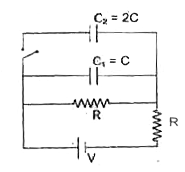
Charge on C2 just after closing the switch is
View Solution
