The carrier freqeuncy of a station is 40 MHz. A resistor of 10k Ω and capacitor of 12 pF are available in the detector circuit. The possible value of C will be
12
8.2
5.6
All of these
The correct Answer is:D
To solve the problem, we need to determine the possible values of capacitance (C) in the detector circuit based on the given parameters: a carrier frequency (Vc) of 40 MHz and a resistor (R) of 10 kΩ.
1. Convert the given values to standard units:
- The carrier frequency (Vc) is given as 40 MHz. We convert this to Hertz (Hz):
Vc=40 MHz=40×106 Hz=4×107 Hz
- The resistance (R) is given as 10 kΩ, which is:
R=10 kΩ=10×103 Ω=104 Ω
- The capacitance (C) is given as 12 pF, which is:
C=12 pF=12×10−12 F
2. Calculate the time period (Tc) of the carrier frequency:
- The time period (Tc) is the reciprocal of the frequency (Vc):
Tc=1Vc=14×107 seconds
- Performing the calculation:
Tc=2.5×10−8 seconds
3. Calculate the time constant (τ) of the RC circuit:
- The time constant (τ) is given by the product of resistance (R) and capacitance (C):
τ=R×C
- Substituting the values:
τ=104 Ω×12×10−12 F=1.2×10−7 seconds
4. Compare the time period (Tc) and time constant (τ):
- For the circuit to be suitable for detection, the time period (Tc) must be less than the time constant (τ):
Tc<τ
- Substituting the calculated values:
2.5×10−8<1.2×10−7
- This inequality holds true, indicating that the circuit is capable of detecting the signal.
5. Determine the possible values of capacitance (C):
- Since the calculated τ is greater than Tc, any value of capacitance that keeps τ greater than Tc is acceptable. Thus, the possible values of C can include the given 12 pF and potentially other values as well.
6. Conclusion:
- The possible values of capacitance (C) in the detector circuit can be any value that satisfies the condition τ>Tc. Therefore, all the options provided (if any) can be valid.
- The carrier frequency (Vc) is given as 40 MHz. We convert this to Hertz (Hz):
Vc=40 MHz=40×106 Hz=4×107 Hz
- The resistance (R) is given as 10 kΩ, which is:
R=10 kΩ=10×103 Ω=104 Ω
- The capacitance (C) is given as 12 pF, which is:
C=12 pF=12×10−12 F
- The time period (Tc) is the reciprocal of the frequency (Vc):
Tc=1Vc=14×107 seconds
- Performing the calculation:
Tc=2.5×10−8 seconds
- The time constant (τ) is given by the product of resistance (R) and capacitance (C):
τ=R×C
- Substituting the values:
τ=104 Ω×12×10−12 F=1.2×10−7 seconds
- For the circuit to be suitable for detection, the time period (Tc) must be less than the time constant (τ):
Tc<τ
- Substituting the calculated values:
2.5×10−8<1.2×10−7
- This inequality holds true, indicating that the circuit is capable of detecting the signal.
- Since the calculated τ is greater than Tc, any value of capacitance that keeps τ greater than Tc is acceptable. Thus, the possible values of C can include the given 12 pF and potentially other values as well.
- The possible values of capacitance (C) in the detector circuit can be any value that satisfies the condition τ>Tc. Therefore, all the options provided (if any) can be valid.
Topper's Solved these Questions
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - NCERT
9 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - CORNER
15 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - Assertion And Reason
30 Videos
- ATOMS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ATOMS EXERCISE - Assertion And Reason
15 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Assertion And Reason
15 Videos
Similar Questions
An inductor of 10mH is connected to a 18V battery through a resistor of 10kΩ and a switch After a long time, when the maximum current is set up in the circuit, the current is switched off. Calculate the cur- rent in the circuit after 2 μs.
View SolutionAn a.c. source of angular frequency ω is fed across a resistor R and a capacitor C in series. The current registered is I. If now the frequency of the source is changed to ω/3 (but maintaining the same voltage), the current in the circuit is found to be halved. calculate the ratio of reactance to resistance at the original frequency ω.
View Solution
Knowledge Check
The carrier freqeuncy of a station is 40 MHz. A resistor of 10k Ω and capacitor of CpF are available in the detector circuit. The possible value of C will be
A12B8.2C5.6DAll of theseIn a diode AM detector with the output circuit consists of R=1MΩ and C=1pF would be more suitable for detecting a carrier signal of
A1MHzB0.1 MHzC0.5MHzD10MHzA 0.2kΩ resistor and 15μF capacitor are connected in series to a 220 V, 50 Hz ac source. The impadance of the circuit is
A250ΩB268ΩC29.15ΩD291.5Ω
The natural frequency of an LC- circuit is 1,25,000 cycles per second. Then the capacitor C is replaced by another capacitor with a dielectric medium of dielectric constant k. In this case, the frequency decreases by 25 kHz. The value of k is
View SolutionAn alternating e.m.f of 220V is applied to a circuit containing a resistor R having resistance of 160Ω and a capacitor .C. in series. The current is found to lead the supply voltage by an angle θ=tan−1(3/4)
Calculate: Impedance of the circuit
View SolutionAn alternating e.m.f of 220V is applied to a circuit containing a resistor R having resistance of 160Ω and a capacitor .C. in series. The current is found to lead the supply voltage by an angle θ=tan−1(3/4)
Calculate: Current flowing in the circuit
View SolutionIn a diode detector , output circuit consists of R=1MωandC=1pF. Calculate the carrier frequency it can detect.
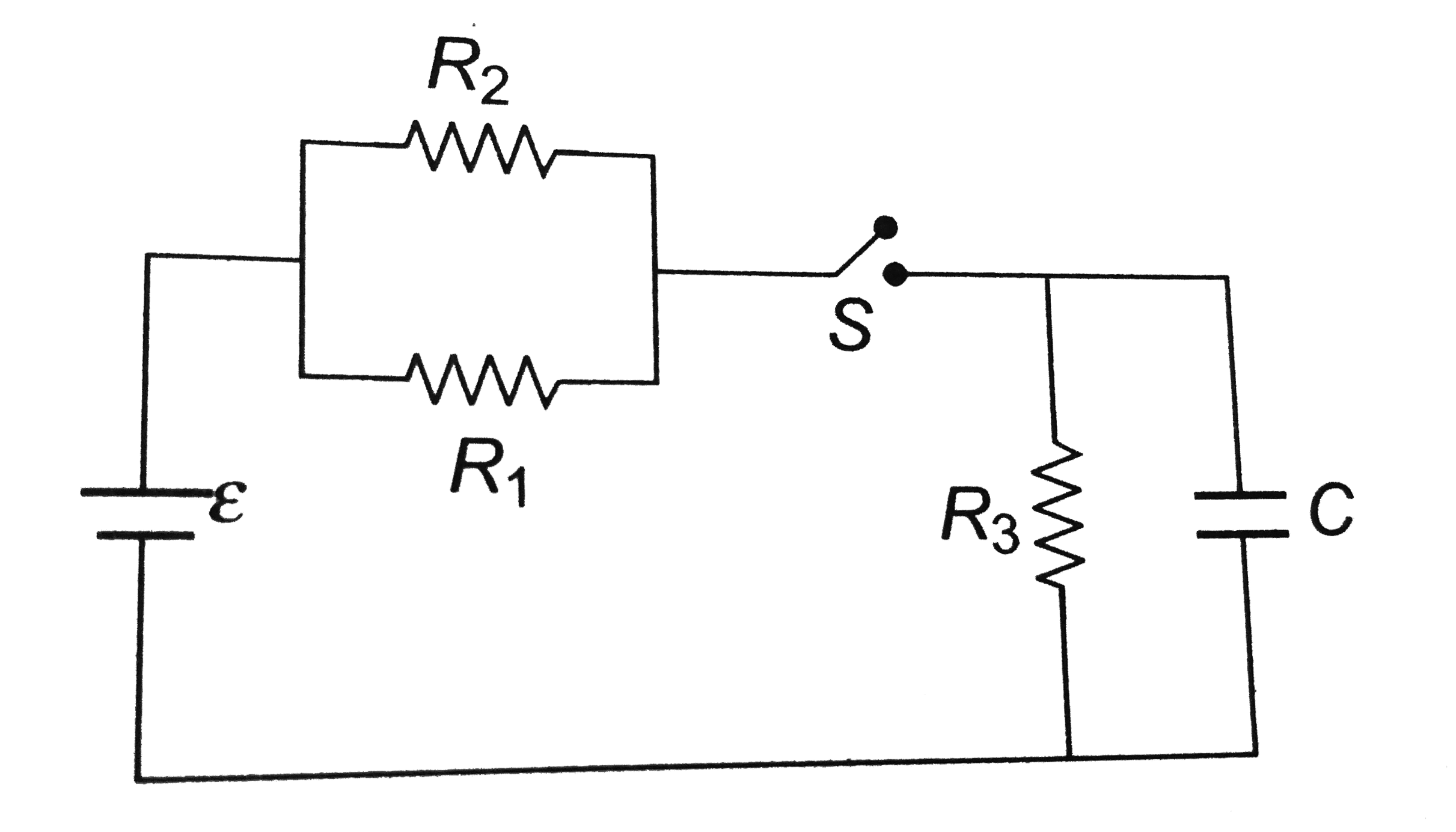
View SolutionThe circuit shown in the figure consists of a battery of emf ε=10V , a capacitor of capacitance C=1.0μF and three resistors of value R1=2Ω,R2=2Ω and R3=1Ω, Initially the capacitor is completely uncharged and the switch S is open. The switch S is closed at t=0. Then
View Solution
