The ceiling of a long hall is 25m high. What is the maximum horizontal distance if a ball thrown with a speed of 40ms−1 can go without hitting the ceiling of the hall ?
To solve the problem of finding the maximum horizontal distance a ball can travel without hitting the ceiling of a hall that is 25 m high, when thrown with a speed of 40 m/s, we can break down the solution into several steps.
Step 1: Understand the motion of the ball
The ball is thrown with an initial speed v0=40m/s. The motion can be analyzed in two dimensions: horizontal and vertical.
Step 2: Determine the maximum height of the ball
The maximum height hmax reached by the ball can be expressed using the formula:
hmax=v20sin2α2g
where g is the acceleration due to gravity (approximately 10m/s2) and α is the angle of projection.
Step 3: Set the maximum height equal to the ceiling height
Since the maximum height must not exceed the height of the ceiling (25 m), we set:
v20sin2α2g=25
Substituting v0=40m/s and g=10m/s2:
402sin2α2×10=25
This simplifies to:
1600sin2α20=25
80sin2α=25
sin2α=2580=516
Taking the square root gives:
sinα=√54
Step 4: Calculate cosα
Using the Pythagorean identity sin2α+cos2α=1:
cos2α=1−sin2α=1−516=1116
Thus,
cosα=√114
Step 5: Calculate the range R
The range R of the projectile can be calculated using the formula:
R=v20sin2αg
Using the identity sin2α=2sinαcosα:
R=v20⋅2sinαcosαg
Substituting the values:
R=402⋅2⋅√54⋅√11410
This simplifies to:
R=1600⋅2⋅√551610=3200⋅√55160=20⋅√55
Calculating √55≈7.416:
R≈20⋅7.416≈148.32m
Final Answer
Thus, the maximum horizontal distance the ball can travel without hitting the ceiling is approximately:
R≈148m
The ball is thrown with an initial speed v0=40m/s. The motion can be analyzed in two dimensions: horizontal and vertical.
The maximum height hmax reached by the ball can be expressed using the formula:
hmax=v20sin2α2g
where g is the acceleration due to gravity (approximately 10m/s2) and α is the angle of projection.
Since the maximum height must not exceed the height of the ceiling (25 m), we set:
v20sin2α2g=25
Substituting v0=40m/s and g=10m/s2:
402sin2α2×10=25
This simplifies to:
1600sin2α20=25
80sin2α=25
sin2α=2580=516
Taking the square root gives:
sinα=√54
Using the Pythagorean identity sin2α+cos2α=1:
cos2α=1−sin2α=1−516=1116
Thus,
cosα=√114
The range R of the projectile can be calculated using the formula:
R=v20sin2αg
Using the identity sin2α=2sinαcosα:
R=v20⋅2sinαcosαg
Substituting the values:
R=402⋅2⋅√54⋅√11410
This simplifies to:
R=1600⋅2⋅√551610=3200⋅√55160=20⋅√55
Calculating √55≈7.416:
R≈20⋅7.416≈148.32m
Thus, the maximum horizontal distance the ball can travel without hitting the ceiling is approximately:
R≈148m
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - EXERCISE32videos
MOTION IN A PLANE
- BOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE21videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERT ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISE28videos
MOTION IN A STRAIGHT LINE
Similar Questions
The ceiling of a long hall is 20m high. What is the maximum horizontal distance that a ball thrown with a speed of 40m can go without hitting the ceiling of hall (g=10ms−2) ?
View SolutionThe ceiling of a tunnel is 5 m high. What is the maximum horizontal distance that a ball thrown with a speed of 20ms−1 can go without hitting the ceiling of the tunnel (g=10ms−2)
View Solution
Knowledge Check
- Question 1 - Select One
The ceiling of a hall is 40m high. For maximum horizontal distance, the angle at which the ball may be thrown with a speed of 56ms−1 without hitting the ceiling of the hall is
A25∘B30∘C45∘D60∘ - Question 2 - Select One
A cricketer can throw a ball to a maximum horizontal distance of 100m. With the same speed how much high above the ground can the cricketer throw the same ball?
A50 mB100 mC150 mD200 m
A cricketer can throw a ball to a maximum horizontal distance of 150 m. With the same speed how high above the ground can the cricketer throw the ball?
View SolutionThe maximum height attained by a ball projected with speed 20ms−1 at an angle 45∘ with the horizontal is [take g = 10ms−2]
View SolutionA cricketer can throw a ball to a maximum horizontal distance of 100m. With the same speed how much high above the ground can the cricketer throw the same ball?
View SolutionA ball is thrown downwards with a speed of 20ms−1, from the top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30ms−1 from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2))
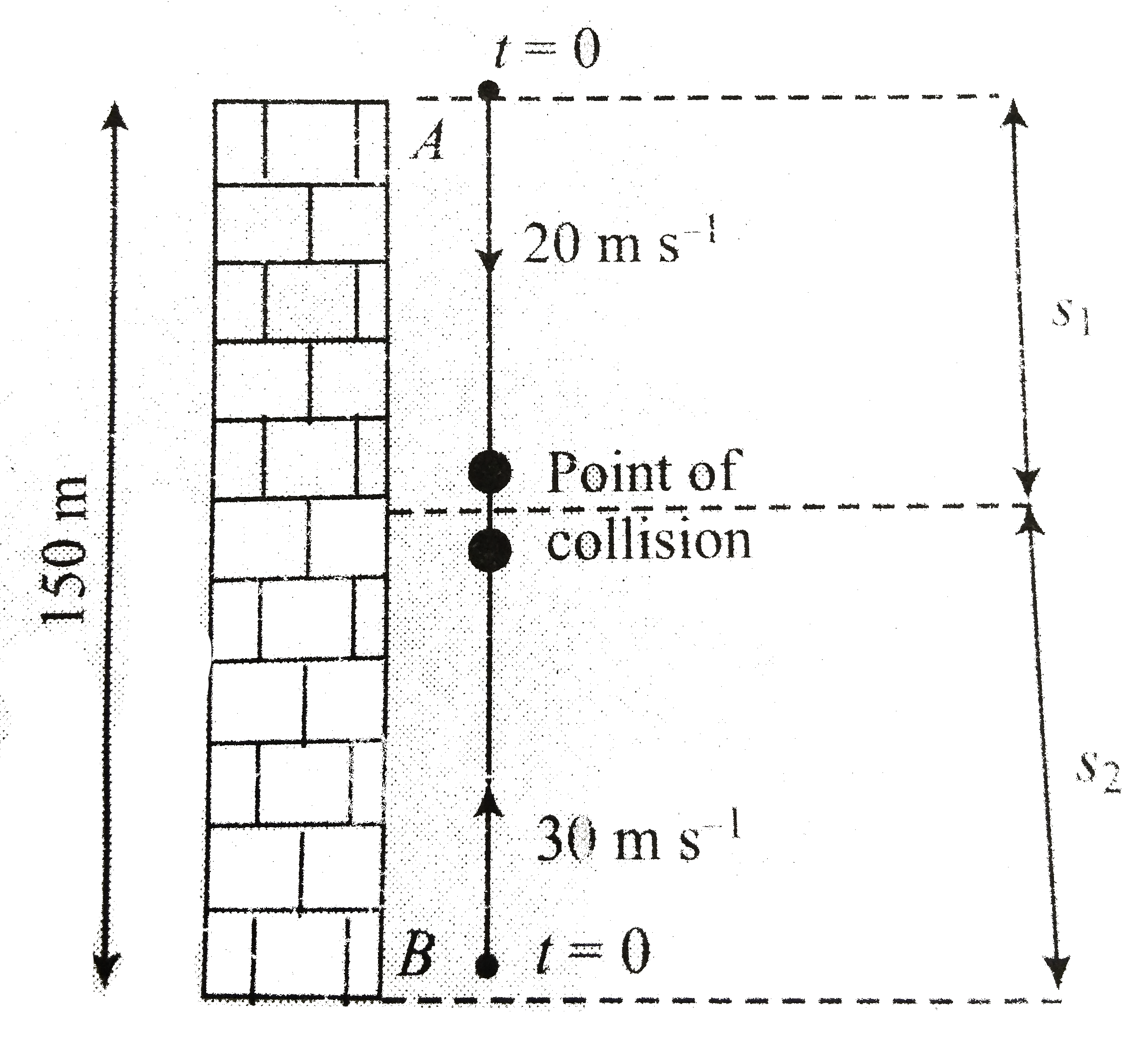 .View Solution
.View SolutionA ball is dropped from the top of a building 100 m high. At the same instant another ball is thrown upwards with a velocity of 40ms−1 from the bottom of the building. The two balls will meet after.
View SolutionA ball is dropped from the top of a building 100 m high. At the same instant another ball is thrown upwards with a velocity of 40ms−1 from the bottom of the building. The two balls will meet after.
View Solution

