The change in the entropy of a 1 mole of an ideal gas which went through an isothermal process form an initial state (P1,V1,T) to the final state (P2,V2,T) is equal to
Zero
R In T
R lnV1V2
R lnV2V1
The correct Answer is:D
The Change in entropy of an ideal gas ,
ΔS=ΔQT ….(i)
In isothermal process , there is no change in internal energy of gas , I .e ΔU=0
∴ ΔU=ΔQ−W
⇒ 0=ΔQ−W⇒ΔQ=W
i.e ΔQ = work done by gas in isothermal process which went through an isothermal process from (p1,V1T) to (p2,V2,T)
or ΔQ=μRTloge(V2V1) (ii)
For 1 mole of an ideal gas , μ=1
So, from Eqs. (i) and (ii) ,we get
or ΔS=Rloge(V2V1)=RIn(V2V1)
Topper's Solved these Questions
- KINETIC THEORY OF GASES ANDRADIATIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - KINETIC THEORY OF GASES ANDRADIATIONEXERCISE - Exercise 2
50 Videos
- KINETIC THEORY OF GASES ANDRADIATIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - KINETIC THEORY OF GASES ANDRADIATIONEXERCISE - MHT CET Corner
40 Videos
- KINETIC THEORY OF GASES ANDRADIATIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - KINETIC THEORY OF GASES ANDRADIATIONEXERCISE - MHT CET Corner
40 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHT BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHT EXERCISE - MHT CET Corner
24 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENTBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENTEXERCISE - MHT CET CORNER
20 Videos
Similar Questions
One mole of an ideal gas expands adiabatically from w an initial state (?A,?0) to final state (?_f, 5V_0).A¬hermo≤ofthesamegasexpandsisothermallyomad⇔erent∈itialstate(?B,?0)→thesamef∈alstate(?_f 5V_0).Theratioofthespecificheatsatconstantpressureandconstantvolumeofthisalgasisgamma.WˆistheratioT_A/T_B?
View SolutionWhen a sample of ideal gas is changed from an initial state to a final state, various curves can be plotted for the process like P-V curve, V-T curve,P-T curve etc.
For example, P-V curve for a fixed amount of an ideal gas at constant temperature is a rectangular hyperbola, V-T curve for a fixed amount of an ideal gas at constant volume is again a straight line. However, the shapes may vary if the constant parameters are also changed.
Now, answer the following questions :
Two moles of an ideal gas is changed from its initial state (16 atm, 6L) to final state (4 atm, 15L) in such a way that this change can be represented by a straight line in P-V curve.The maximum temperature attained by the gas during the above change is :(Take : R=112LatmK−1mol−1)
View Solution
Knowledge Check
The change in the entropy of a 1 mole of an ideal gas which went through an isothermal process form an initial state (P1,V1,T) to the final state (P2,V2<T) is equal to
AzeroBR ln TCR ln V1V2DRln(V2)V1The change in entropy when the pressure of perfect gas is changed isothermally from P1 to P2 is
A△S=nRln(P1+P2)B△S=nRln(P2/P1)C△S=nRln(P1/P2)D△S=nRln(P1+P2P2)One mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P1,V1,T1) to the final state (P2,V2,T2). The decrease in the internal energy of the gas during this process will be given by
ACV(T1−T2)BCP(T1−T2)CCP+CV2(T1−T2)D(CP−CV)(T1−T2)
The state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is p02, then the pressure of the gas in state C is
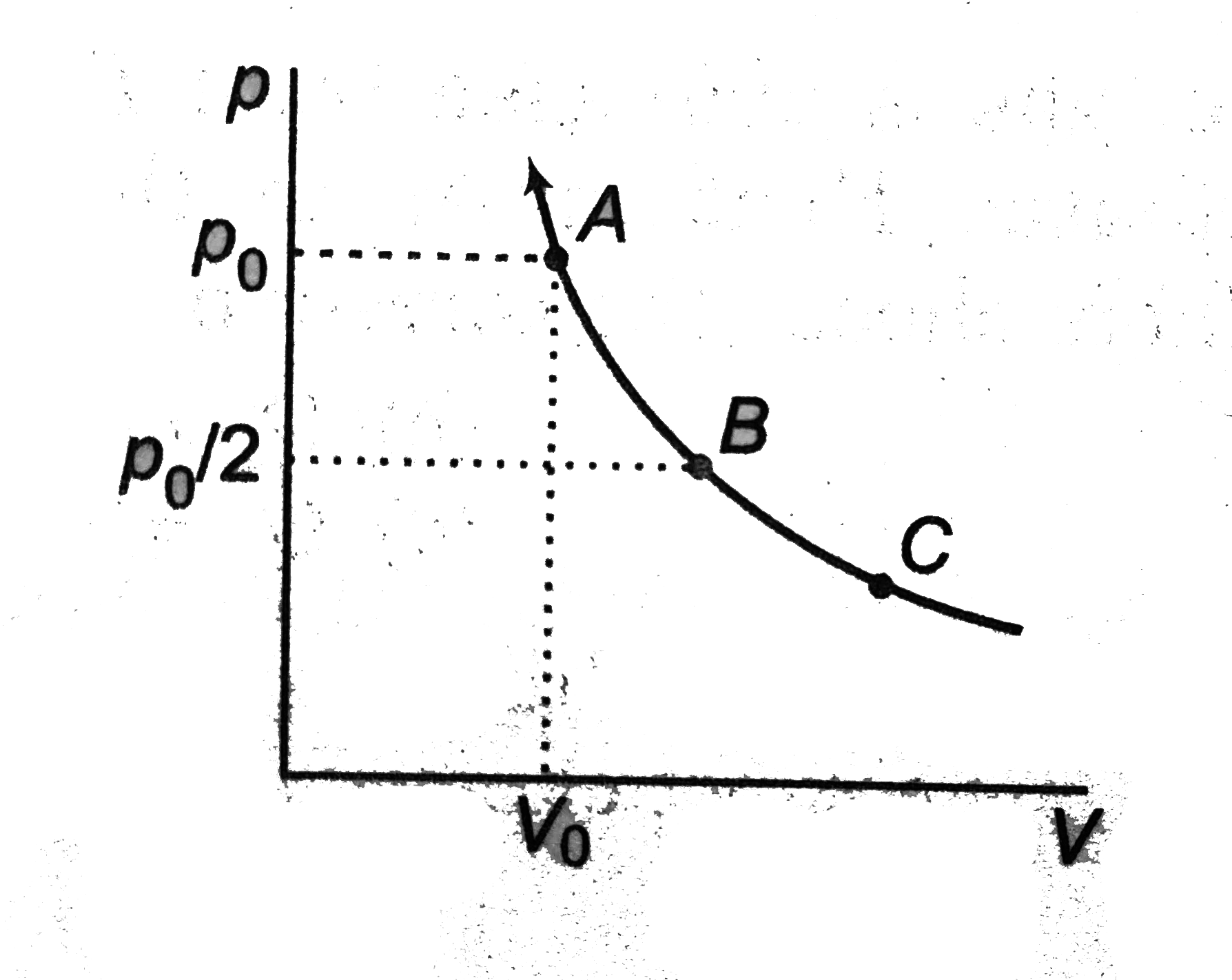
View SolutionIf n moles of an ideal gas are expanded is isothermally and reversibly from an initial state in which it has pressure p1 and volume V1 to the final state of volume V2 and pressure P2, then
View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
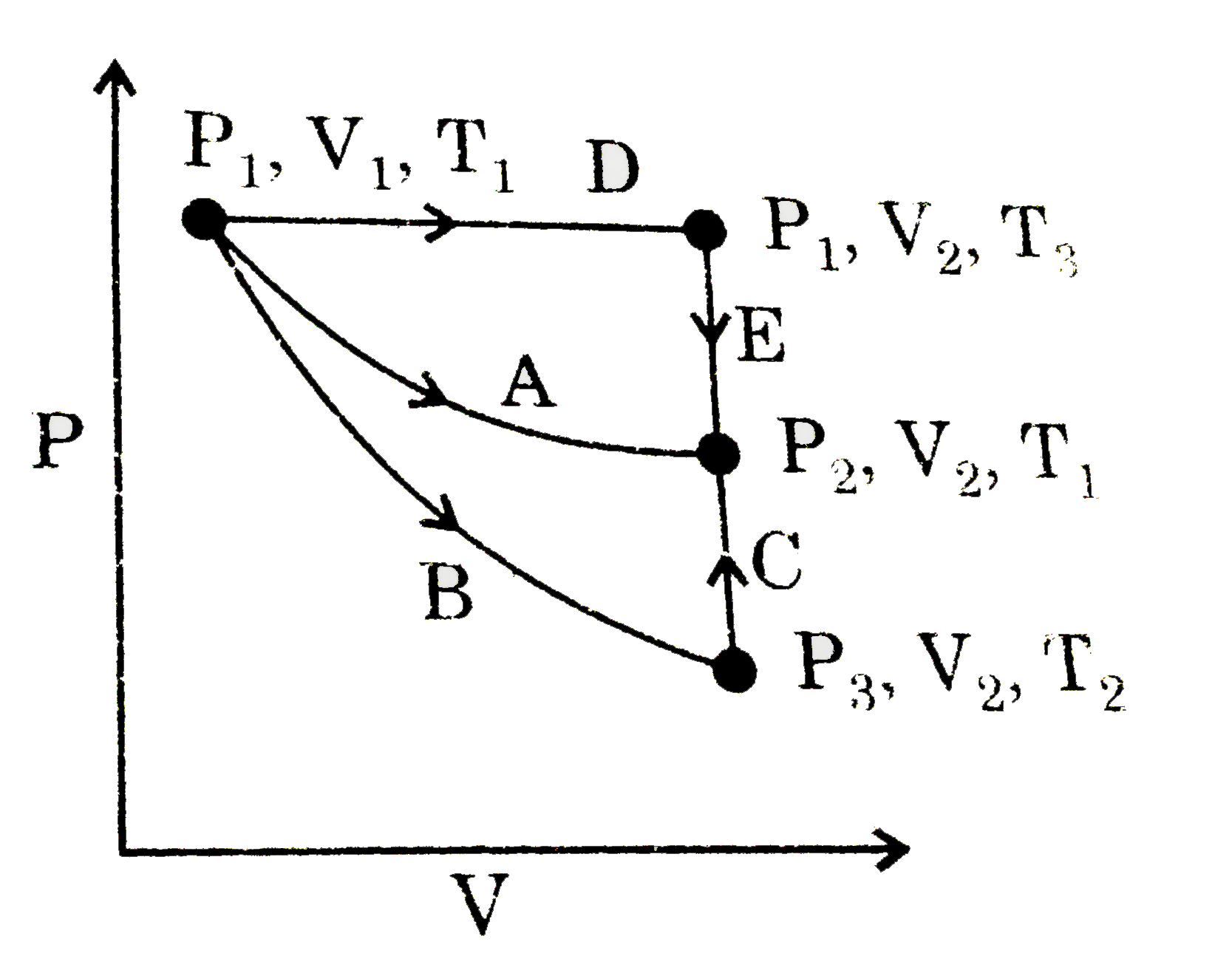
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is qrev for path (A)?
View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
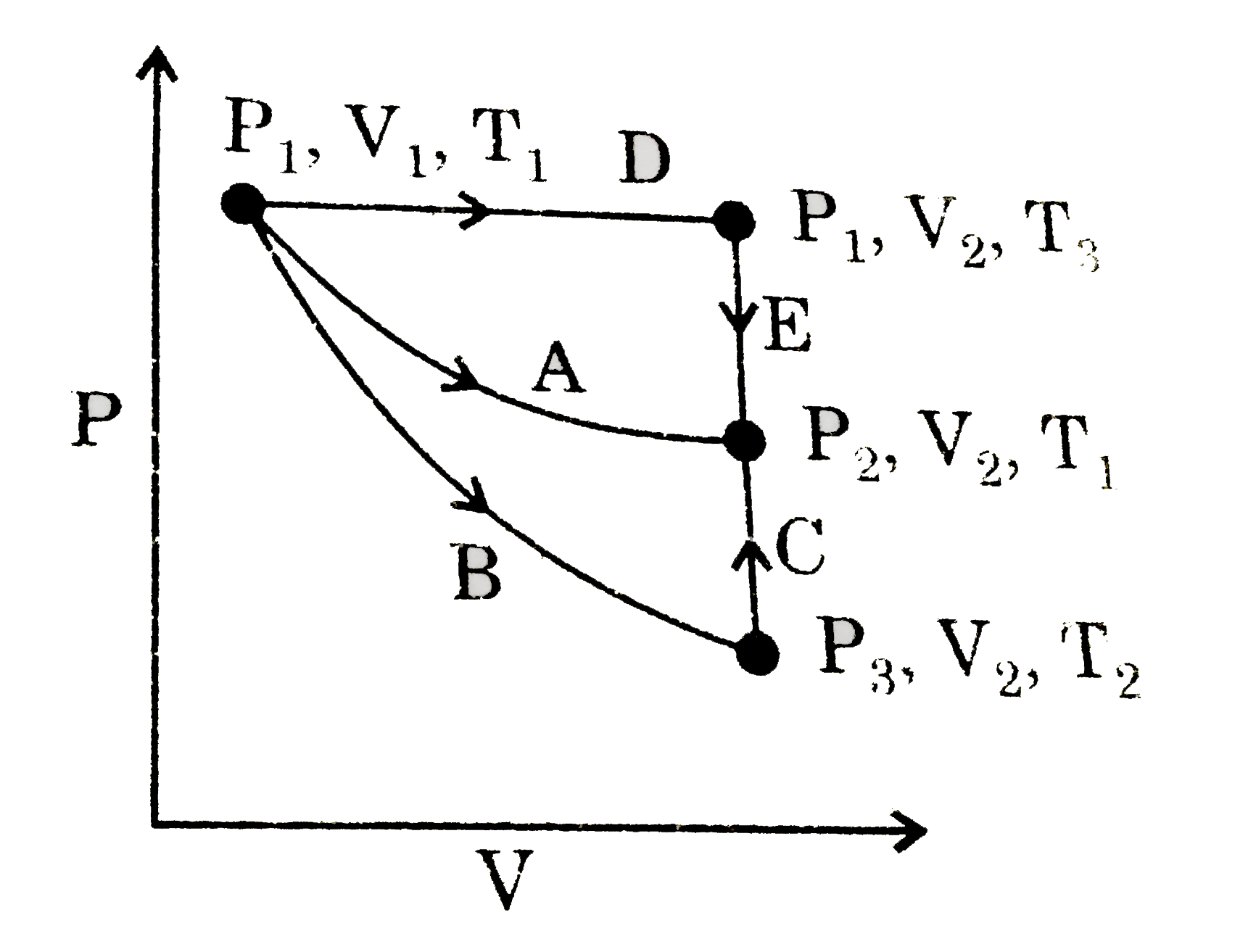
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for (D+E)?
View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .

Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for path (A)?
View Solution
