The compensated pendulum of a clock consista of an isosceles triangular frame of base length l1 and expansivity α1 and side length l2 and expansivity α2. The pendulum is supported as shown in the figure. Calculate the ratio l1/l2 so that the length of the pendulum may remain unchanged at all temperatures?

The correct Answer is:l1l2=2√α2α1
Topper's Solved these Questions
Similar Questions
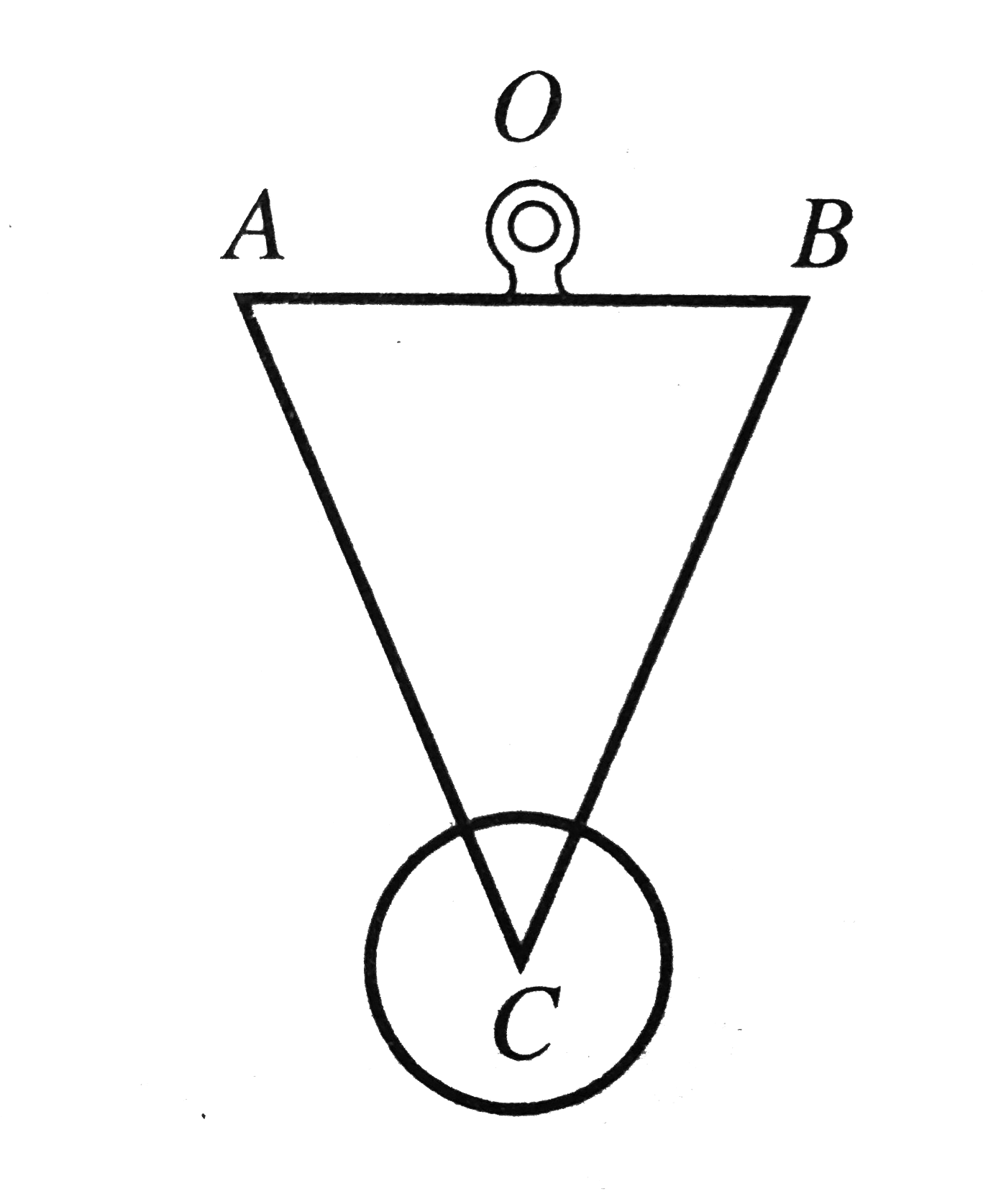
A compensated pendulum shown if Fig. is in the from of an isosceles Delta of base length l1=5cm and coefficent of linar expansion α1=18×10−6 and side length l2 and coefficient of linear expansion α2=12×10−6. find l2 so the the distance of centre of mass of the bob from suspension centre O may remain the same at all the temperature.
View Solution
A compensated pendulum shown if Fig. is in the from of an isosceles Delta of base length l1=5cm and coefficent of linar expansion α1=18×10−6 and side length l2 and coefficient of linear expansion α2=12×10−6. find l2 so the the distance of centre of mass of the bob from suspension centre O may remain the same at all the temperature.
View Solution
Knowledge Check
The l−T2 graph of a simple pendulum is an shown in the figure. The time period of the pendulum of length 0.5 mm is
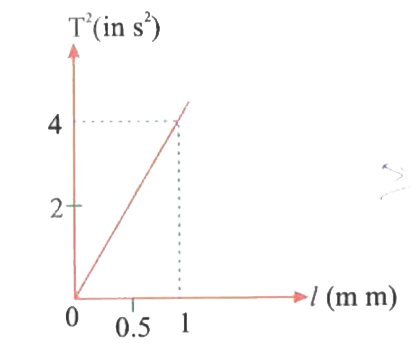 A1sB1.2 sC√2 sD1√2s
A1sB1.2 sC√2 sD1√2sIf l1 and l2 are the lengths of a seconds pendulum at the poles and the equator of the earth, then
Al1>l2Bl1<l2Cl1=l2Dl1=0.9l2An isosceles triangle is formed with a thin rod of length l1 and coefficient of linear expansion α1, as the base and two thin rods each of length l2 and coefficient of linear expansion α2 as the two sides. The distance between the apex and the midpoint of the base remain unchanged as the temperature is varied. the ratio of lengths l1l2 is
 A2√α1α2B√α2α1C2√α2α1D12√α2α1
A2√α1α2B√α2α1C2√α2α1D12√α2α1
An isosceles triangles is formed with a thin rod of length l1 and coefficient of linear expansion α1, as the base and two thin rods each of length l2 and coefficient of linear expansion α2 as the two sides. The distance between the apex and the midpoint of the base remain unchanged as the temperature is varied. the ratio of lengths l1l2 is

View SolutionAn isosceles triangles is formed with a thin rod of length l1 and coefficient of linear expansion α1, as the base and two thin rods each of length l2 and coefficient of linear expansion α2 as the two sides. The distance between the apex and the midpoint of the base remain unchanged as the temperature is varied. the ratio of lengths l1l2 is

View SolutionAn isosceles triangles is formed with a thin rod of length l1 and coefficient of linear expansion α1, as the base and two thin rods each of length l2 and coefficient of linear expansion α2 as the two sides. The distance between the apex and the midpoint of the base remain unchanged as the temperature is varied. the ratio of lengths l1l2 is

View SolutionIn a compensated pendulum a triangular frame ABC is made using two different metals. AB of length l1 is made using a metal having coefficient of linear expansion α1. BC and AC of length l2 each have coefficient of linear expansion α2. A heavy bob is attached at C. Pendulum can oscillate about the pivot D. Find l2l1 so that distance of bob from the pivot point D does not change with change in temperature.
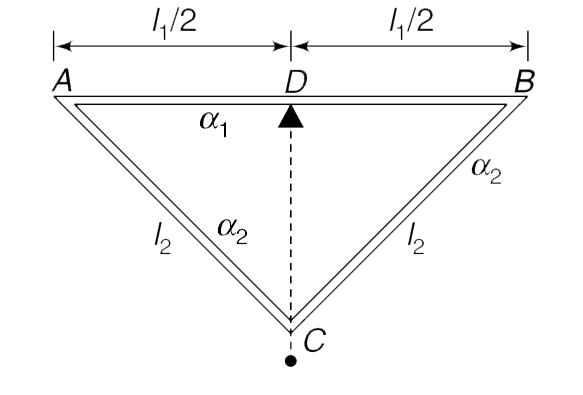
View SolutionIn the shown planar frame made of thin uniform rods, the length of section AB and EF is l1 and its thermal linear coefficient of expansion is α1. The length of section CD is l2 and its thermal linear coefficient of expansion is α2.CBandDE are of same length having thermal linear coefficient of expansion α2. point A,B,EandF reside on same line, that is, sections ABandEF overlap. then the ratio of l1l2 for which the distance between end A and end F remains the same at all temperatures, is

View Solution
