The conducting circular loops of radii R1andR2 are placed in the same plane with their centres coinciding. If R1>>R2, the mutual inductance M between them will be directly proportional to
R1R2
R2R1
R21R2
R22R1
The correct Answer is:D
Let acurrent I1 flows through the outer circular col of radius R1.
The magnetic field at the centre of the coil is
B1=μ0I12R1
As the inner coil of radius R1placed co-axiallu has small radius (R2−R1), therefore, B1 may be takne constant over its corss-sectional area.
Hence, flux associated with the inne coil is
ϕe2B1πR22=μ0I12R1πR22
As M=ϕ2I1=μ0R222R1
∴M∝(R22))R1
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION AND REASON
15 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Two conducting circular loops of radii R1andR2 are placed in the same plane with their centres coincidingt. Find the mutual inductane between them assuming R2<<R1.
View SolutionTwo concentric circular coils of radius r and R are placed coaxially with centres coinciding If R>>r then calculate the mutual inductance the coils.
View SolutionThree plates A, B and C are placed close to each other with +Q charge given to the middle plate. The inner surfaces to A and C can be connected to earth through plate D and keys K1 and K2 . The plates D is a dielectric slab with dielectric constant K1 then the charge that will flow through plate D and keys K1 and K2 . The plate D is a dielectric slab with dielectric constant K, then the charge that will flow though plate D when K2 is closed and K2 is open is
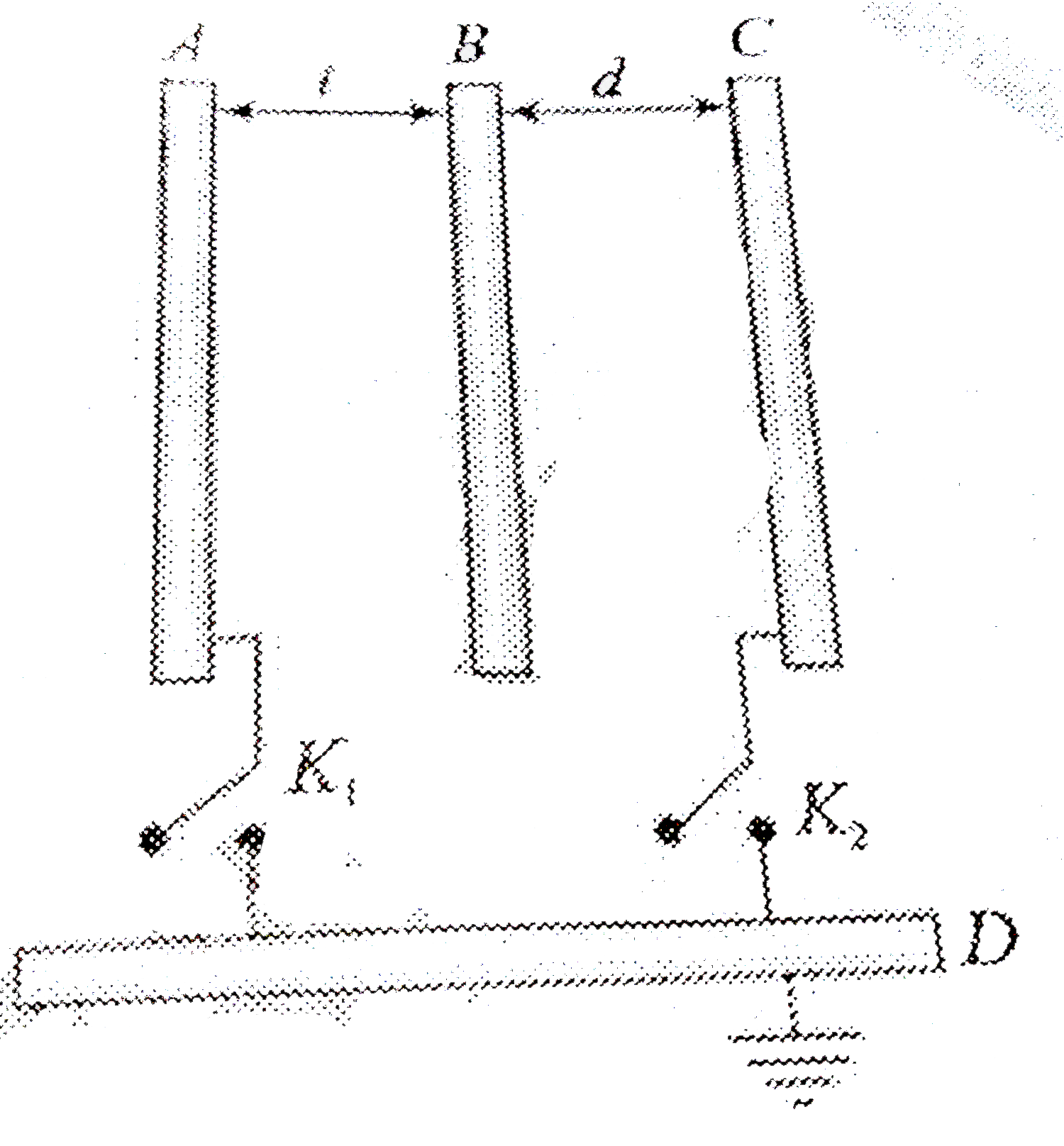
View SolutionTwo circular coils, one of smaller radius r1 and the other of very large radius r2 are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionTwo thin metallic spherical shells of radii r1 and r2 (r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells is maintained at temperature θ1 .and the outer shell at temperature θ2 (θ1<θ2). Calculate the rate at which heat flows radially through the material.

View SolutionTwo thin metallic spherical shells of radii r1 and r2 (r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells is maintained at temperature θ1 and the outer shell at temperature θ2 (θ1<θ2). Calculate the rate at which heat flows radially through the material.

View SolutionSpheres of the same material and same radius r are touching each other. Show that gravitational force between them is directly proportional to r4.
View SolutionSpheres of the same material and same radius r are touching each other. Show that gravitational force between them is directly proportional to r4.
View SolutionA small coil of radius r is placed at the centre of a large coil of radius R, where R>>r. The two coils are coplanar. The mutual inductance between the coils is proportional to
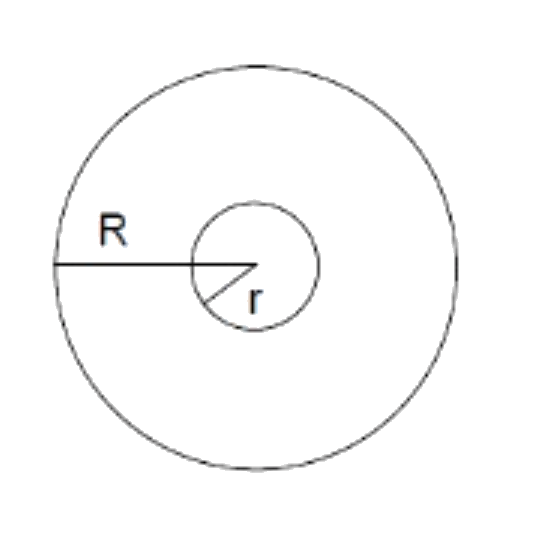
View SolutionTwo concentric co - planar circular loops of radius R and r(<<R) are placed as shown in the figure. The mutual inductance of the system will be
View Solution
