The current in an ideal, long solenoid is varies at a uniform rate of 0.01As−1. The solenoid has 2000 turns/m and its radius 6.0 cm. (a) Consider a circle of radius 1.0 cm inside the solenoid with its axis coinciding with the axis of the solenoid. write the change in the magnetic flux through this circle in 2.0 seconds. (b) find the electric field induced at a point on the circumference of hte circle. (c) find the electric field induced at a piont outside the solenoid at a distance 8.0cm from its axis.
Solenoid: n=2000/m
didt=0.01A/sec implies di=0.01dt
(a) Magnetic field due to solenoid
B=μ0ni
Flux through circle of radius r
ϕ=Bπr2=μoniπniπr2
dϕ=μ0nπr2i
=μnπr2(0.01)dt
ϕμ0nπr2(0.01)∫20dt
=4π×10−7×2000×π(0.1)2(0.01)×2
=4π2×400010−13=16×10−9 weber
(b) ∮→E.→dt=dϕdt
E.2πr=μ0nπr2didt
E=μ0nr2didt
=4π×10−7×200×0.12×0.1
=4π×10−8V/m
∮→E.→dt=ddt(μniπR2)
E=μnR22rdidt
=4π×10−7×2000×(0.6)2×0.012×0.08
=18π×10−8N/m
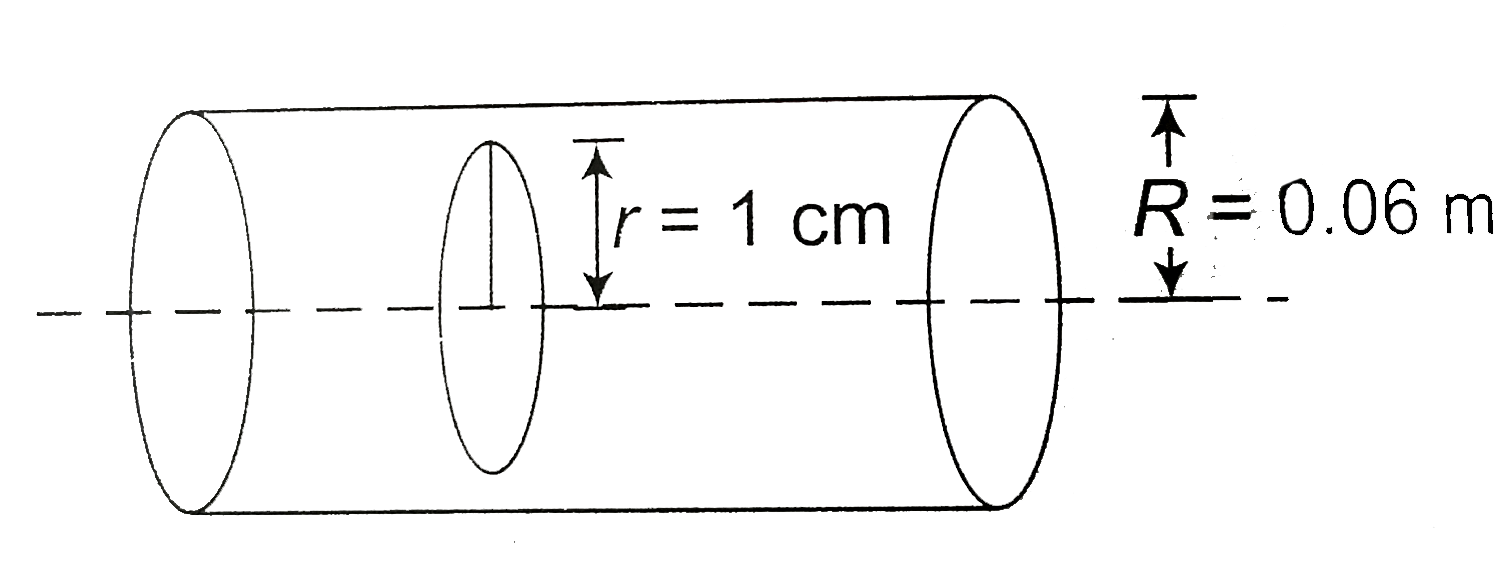
Topper's Solved these Questions
Similar Questions
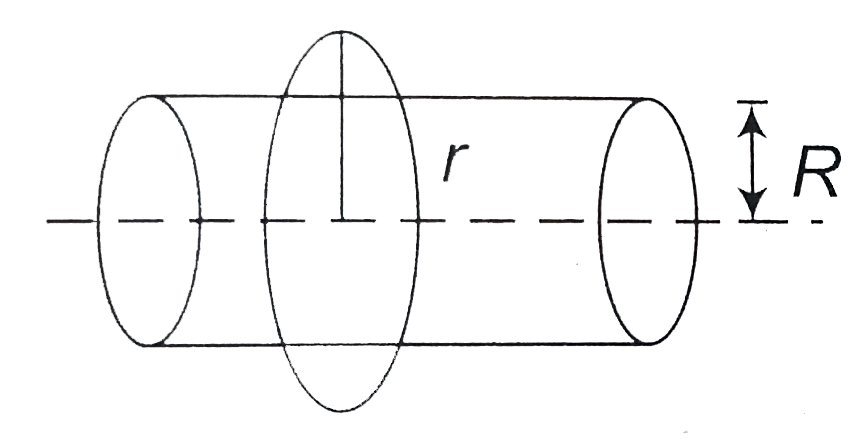
The cruuent in an ideal, long solenoid is varied at a uniform rate of 0.02A/s. The solenoid has 1000 turns/s and its radius is 8 cm.
(i) Consider a circle of radius 2 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 4 s.
(ii) Find the electric field induced at a point on the circumference of the circle.
(iii) Find the electric field induced at a point outside the solenoid at a distance 9 cm from its axis.View SolutionAn air-solenoid has 500 turns of wire in its 40 cm length. If the current in the wire be 1.0 ampere then the magnetic field on the axis inside the solenoid is -
View Solution
Knowledge Check
- Question 1 - Select One
A 0.100 m long solenoid has a radius of 0.050 m and 1.50×104 turns. The current in the solenoid changes at a rate of 6.0 A/s. A conducting loop of radius 0.0200 m is placed at the center of the solenoid with its axis the same as that of the solenoid as shown.
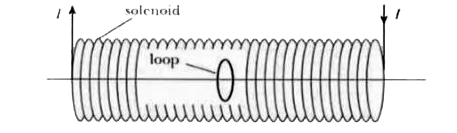
What is the magnetic flux through the small loop when the current through the solenoid is 2.50 A?A2.95×10−2 WbB5.92×10−4 WbC7.28×10−2 WbD4.38×10−4 Wb - Question 2 - Select One
A solenoid of radius R and length L has a current I=I0 cosωt. The value of induced electric field at a distance of r outside the solenoid, is
Aμ0nl0ωR22rsinωtBμ0nl0ωR2rsinωtCμ0nl0R2rsinωtDzero - Question 3 - Select One
A long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
A0.5 secB1.0 secC0.25 secD0.75 sec
A thin solenoid of length 0.4m and having 500 turns of wire carries a current 1A,then find the magnetic field on the axis inside the solenoid.
View SolutionA 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire ?
View SolutionAn 8 cm long wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. If the magnetic field inside the solenoid is 0.3 T, then magnetic force on the wire is
View SolutionA 0.100 m long solenoid has a radius of 0.050 m and 1.50×104 turns. The current in the solenoid changes at a rate of 6.0 A/s. A conducting loop of radius 0.0200 m is placed at the center of the solenoid with its axis the same as that of the solenoid as shown.
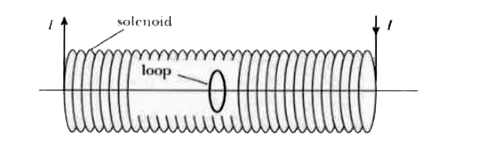
Determine the induced emf in the loop.View SolutionA long solenoid with 10 turn / cm and a radius of 7.0 cm carries a current of 20.0 mA .A current of 6.0 A exists in a straight conductor loacted along the central axis of the solenoid at what radial distance from the axis will the direction of the magneitic field be at 45∘ to the axial direction
View Solution

