The deflection in a moving coil galvanometer falls from 50 divisions to 10 divisions when a shunt of 12 ohm is applied. What is the resistance of the galvanometer?
To solve the problem, we need to find the resistance of the galvanometer (Rg) given the change in deflection when a shunt resistance (Rs) is applied. Here’s a step-by-step solution:
Step 1: Understand the relationship between current and deflection
The deflection in a galvanometer is proportional to the current passing through it. Let:
- I be the current through the galvanometer when the deflection is 50 divisions.
- I′ be the current through the galvanometer when the deflection is 10 divisions.
From the problem, we can express these currents as:
- I=k×50 (1)
- I′=k×10 (2)
where k is a constant of proportionality.
Step 2: Relate the currents
When the shunt resistance Rs=12Ω is connected, the current through the galvanometer changes. The current through the shunt can be expressed as:
- I−I′=Is
From equations (1) and (2), we can express:
- I′=I5 (since I′ is 10 divisions and I is 50 divisions)
Step 3: Calculate the current through the shunt
The current through the shunt Is can be calculated as:
- Is=I−I′=I−I5=4I5
Step 4: Use the relationship of currents in parallel
Since the galvanometer and the shunt are in parallel, we can use the formula for the current through the galvanometer:
- The current through the galvanometer I′ is given by:
I′=VRg
- The current through the shunt Is is given by:
Is=VRs
Since both currents are equal to the voltage across their respective resistances, we can express this as:
I′Is=RsRg
Step 5: Substitute the known values
Substituting I′=I5 and Is=4I5:
I54I5=RsRg
This simplifies to:
14=RsRg
Step 6: Solve for the resistance of the galvanometer
Now substituting Rs=12Ω:
14=12Rg
Cross-multiplying gives:
Rg=12×4=48Ω
Final Answer:
The resistance of the galvanometer Rg is 48 ohms.
---
The deflection in a galvanometer is proportional to the current passing through it. Let:
- I be the current through the galvanometer when the deflection is 50 divisions.
- I′ be the current through the galvanometer when the deflection is 10 divisions.
- I=k×50 (1)
- I′=k×10 (2)
When the shunt resistance Rs=12Ω is connected, the current through the galvanometer changes. The current through the shunt can be expressed as:
- I−I′=Is
- I′=I5 (since I′ is 10 divisions and I is 50 divisions)
The current through the shunt Is can be calculated as:
- Is=I−I′=I−I5=4I5
Since the galvanometer and the shunt are in parallel, we can use the formula for the current through the galvanometer:
- The current through the galvanometer I′ is given by:
I′=VRg
- The current through the shunt Is is given by:
Is=VRs
I′Is=RsRg
Substituting I′=I5 and Is=4I5:
I54I5=RsRg
This simplifies to:
14=RsRg
Now substituting Rs=12Ω:
14=12Rg
Cross-multiplying gives:
Rg=12×4=48Ω
The resistance of the galvanometer Rg is 48 ohms.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA142videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
The deflection in a moving coil galvanometer is
View Solutionthe deflection in a moving coil galvenometre falls from 50 divisions to 10 divisions when a shunt of 12Ω is applied. What is the resistance of the galvenometre? Assume the main current to remain same.
View SolutionThe deflection in a moving coil galvanometer falls from 50 divisions when a shunt of 2Ω is applied. What is the resistance ( in ohms ) of the galvanometer ?
View SolutionThe deflection in a galnometer falls from 50 divisions to 20 divisions, when a 12Ω shunt is applied. The galvanometer resistance is
View SolutionWhen a 12Ω resistor is connected with a moving coil galvanometer, then its deflection reduces form 50 divisions to 10 divisions. The ressitance of the galvanometer is
View SolutionThe deflection in moving coil galvanometer is reduced to half when it is shunted with a 40Ω coil . The resistance of the galvanometer is
View SolutionIf in a moving coil galvanometer, a current I produces a deflection θ, then
View SolutionCurrent senstivity of moving coil galvanometer is 5div/mA and its voltage senstivity (angular deflection per unit voltage applied) is 20div/V. The resistance of the galvanometer is
View SolutionA galvanometer of resistance 20Ω is shunted by a 2Ω resistor. What part of the main current flows through the galvanometer ?
View SolutionA galvanometer of resistance 95Ω, shunted resistance of 5Ω, gives a deflection of 50 divisions when joined in series with a resistance of 20kΩ and a 2V accumulator. What is the current sensitivity of the galvanomter (in div/μA)?
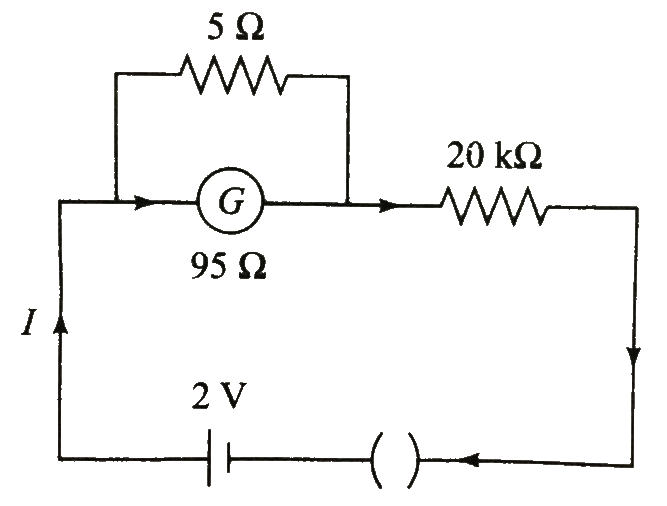 View Solution
View Solution

