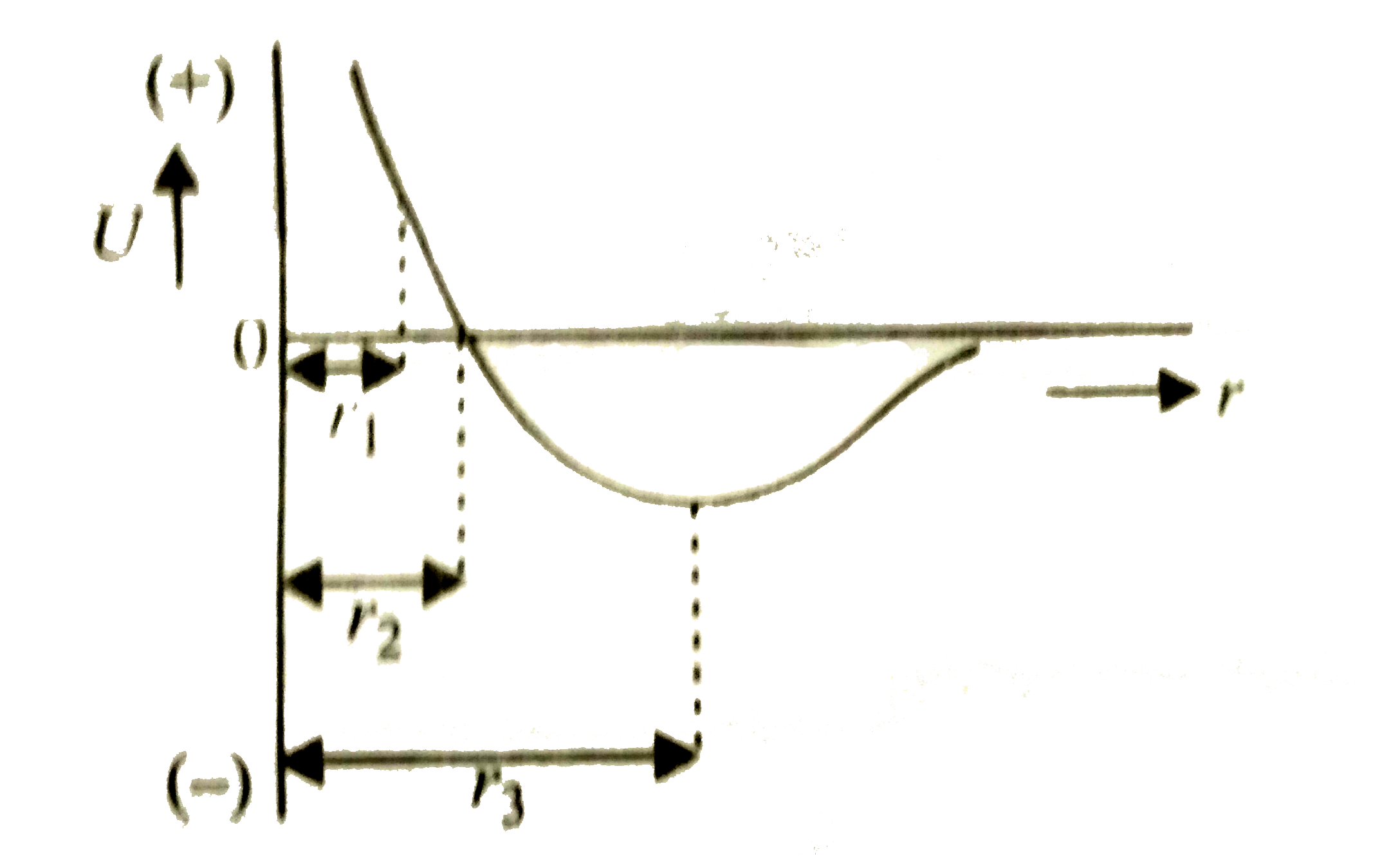
The dependence of tho potential energy W of the interaction between objects on the distance r separating thorn is shown ill t.he figure. What will be the distances between the objects that correspond 1.0 equilibrium positions? At what dislancc will the equilibrium be stable? (Answer the same question for unstable equilibrium.) What segments of the curve correspond to a repulsive force and what segments, to an attractive force?
Step by step video & image solution for The dependence of tho potential energy W of the interaction between objects on the distance r separating thorn is shown ill t.he figure. What will be the distances between the objects that correspond 1.0 equilibrium positions? At what dislancc will the equilibrium be stable? (Answer the same question for unstable equilibrium.) What segments of the curve correspond to a repulsive force and what segments, to an attractive force? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two bodies each of mass 10 kg attract each other with a force of 0.1 milligram weight. What is the distance between them ?
View SolutionThe potential energy of a particle in a certain field has the form U=(a/r2)−(b/r) , where a and b are positive constants and r is the distance from the centre of the field. Find the value of r0 corresponding to the equilibrium position of the particle, examine whether this position is stable.
View Solution
Knowledge Check
The given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them r,
 A1 and 2B1 and 4C2 and 4D2 and 3
A1 and 2B1 and 4C2 and 4D2 and 3The potential energy U of two atoms of a diatomic molecule as a function of distance r between the atoms as shown in the given figure.
Read the following statement carefully.
1. The equilibrium separation distance between the atoms is equal to r2.
2. At r=r1, the force between the atom is repulsive.
3. Forr>r2, the force between the atoms is attractive
Which of the above statements is true ?A1 onlyB2 onlyC3 onlyD2 and 3Two positive point charges are separated by a distance R. If the distance between the charges is reduced to R/2, what happens to the total electric potential energy of the system?
AIt is doubledBIt is reduced to one-half of its original valueCIt remains the sameDIt is reduced to one-fourth of its original value
The potential energy of two atoms separated by a distance x is give by U=−A/x0, where A is a positive constant. What is the force exerted by one atom on another atom ?
View SolutionFor the potential energy curve shown shown in figure.
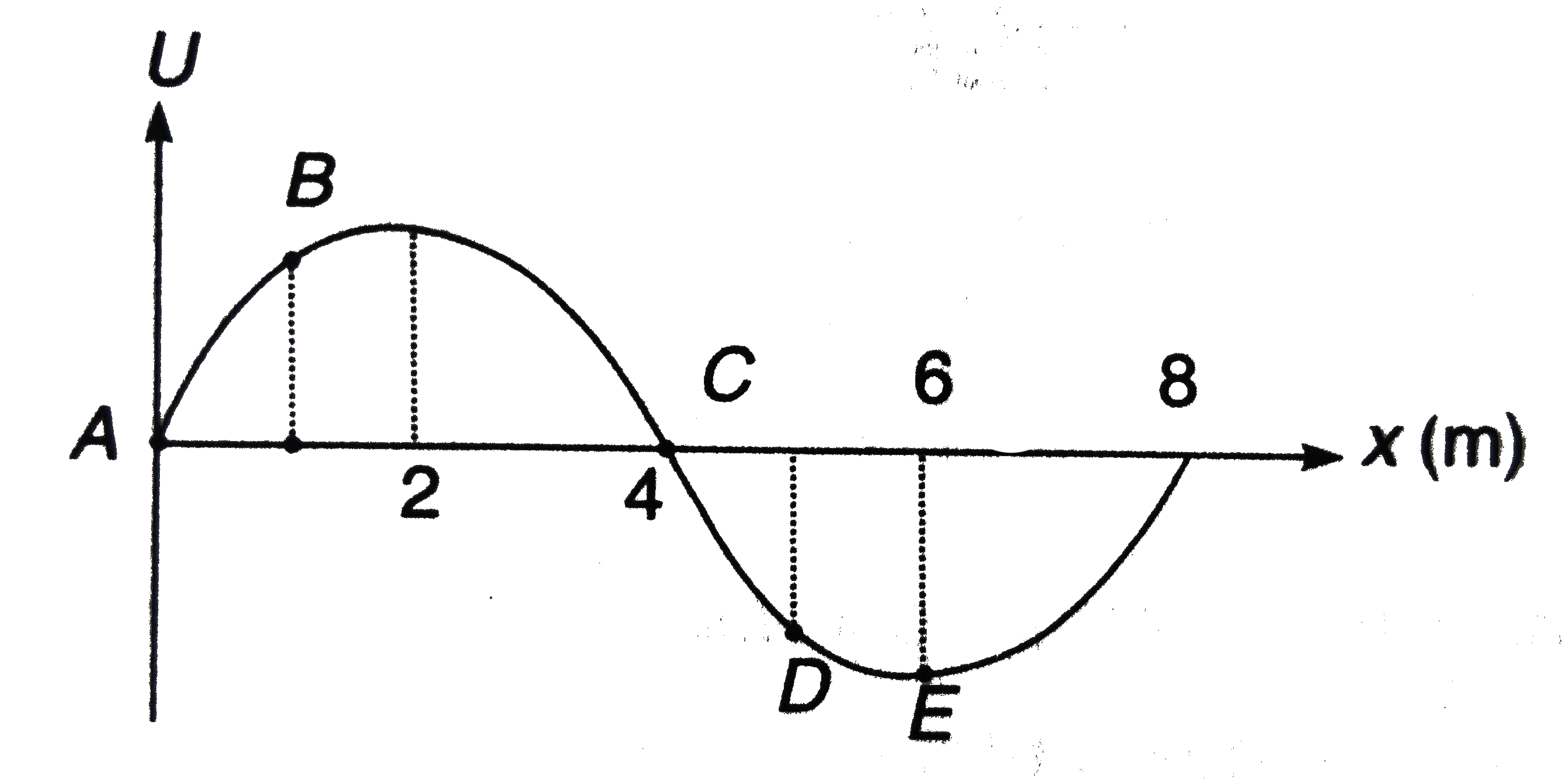
(a) Find directions of force at points A,B,C,D and E.
(b) Find positions of stable, unstable and neutral equilibriums.
View SolutionThe potential energy of a particle in a certain field has the form U=a/r2−b/r, where a and b are positive constants, r is the distance from the centre of the field. Find:
(a) the value of r0 corresponding to the equilibrium position of the particle, examine where this position is steady,
(b) the maximum magnitude of the attraction force, draw the plots U(r) and Fr(r) (the projections of the force on the radius vector r).
View SolutionThe force of attraction (A) between two objects, whose masses are fixed, varies inversely with the square of their distance of separation 9d). The force of attraction between them is 2 units when the distance is 5 cm. what is the distance between the two objects, if the attraction between them is 8 units?
View SolutionThe force of attraction (A) between two objects, whose masses are fixed, varies inversely with the square of their distance of separation 9d). The force of attraction between them is 2 units when the distance is 5 cm. what is the distance between the two objects, if the attraction between them is 8 units?
View Solution
