The dimensions of intensity of wave are
[ML2T−3]
[ML0T−3]
[ML−2T−3]
[M1L2T3]
The correct Answer is:B
Intensity of wave
=EnergyArea×Time=ML2T−2L2T=[ML0T−3]
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Multiple Correct2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Linked Comprehension3videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Subjective31videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
Similar Questions
Knowledge Check
- Question 1 - Select One
The dimensions of intensity of wave are
A[L°MT–3]B[L1M2T–2]C[L2MT–2]D[L2M2T–3] - Question 2 - Select One
The unit of intensity of a wave is Wm2? What are dimensions of intensity of wave?
A[MT−3]B[AML0T−2]C[M0L−1T−2]DNone of these - Question 3 - Select One
The dimensions of magnetic intensity are
A[LI]B[L2I]C[L−1I]D[L−2I]
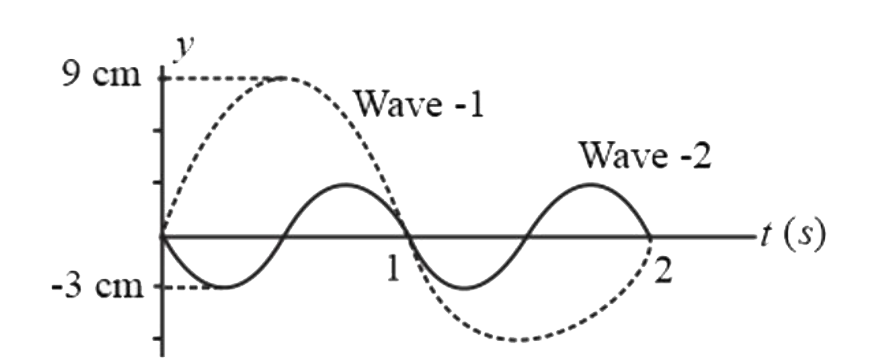
Displacement - time graphs for two waves, wave - 1 and wave - 2 are shown here. The ratio of the intensity of wave-1 to that of wave - 2 is
 View Solution
View SolutionTwo coherent sources produce waves of different intensities which interfere. A fter interference, the ratio of the maximum intensity to the minimum intensity is 16. The intensity of the waves are in the ratio :
View SolutionTwo coherent sources produce waves of different intensities which interfere. A fter interference, the ratio of the maximum intensity to the minimum intensity is 16. The intensity of the waves are in the ratio :
View SolutionThe dimensions of electric intensity are
View SolutionThe ratio of intensity of wave and energy density gives
View Solution


_E01_106_Q01.png)