The distance travelled by the particle is
8 cm
2 cm
4 cm
zero
The correct Answer is:A
To solve the problem of finding the distance traveled by a particle executing simple harmonic motion (SHM) with a given amplitude, we can follow these steps:
1. Understand the Concept of Amplitude:
The amplitude (A) is the maximum distance from the mean position to either extreme position in SHM. In this case, the amplitude is given as 2 cm.
2. Identify the Motion of the Particle:
In one complete oscillation (one time period), the particle moves from the mean position to the maximum positive displacement (A), then back to the mean position, then to the maximum negative displacement (-A), and finally returns to the mean position.
3. Calculate the Distance Traveled in One Complete Oscillation:
- From the mean position to the maximum positive displacement: Distance = A = 2 cm
- From the maximum positive displacement back to the mean position: Distance = A = 2 cm
- From the mean position to the maximum negative displacement: Distance = A = 2 cm
- From the maximum negative displacement back to the mean position: Distance = A = 2 cm
Therefore, the total distance traveled in one complete oscillation is:
Total Distance=A+A+A+A=4A
4. Substitute the Value of Amplitude:
Now, substituting the value of amplitude (A = 2 cm):
Total Distance=4×2 cm=8 cm
5. Conclusion:
The distance traveled by the particle in one time period is 8 cm.
Final Answer:
The distance traveled by the particle in one time period is 8 cm.
---
The amplitude (A) is the maximum distance from the mean position to either extreme position in SHM. In this case, the amplitude is given as 2 cm.
In one complete oscillation (one time period), the particle moves from the mean position to the maximum positive displacement (A), then back to the mean position, then to the maximum negative displacement (-A), and finally returns to the mean position.
- From the mean position to the maximum positive displacement: Distance = A = 2 cm
- From the maximum positive displacement back to the mean position: Distance = A = 2 cm
- From the mean position to the maximum negative displacement: Distance = A = 2 cm
- From the maximum negative displacement back to the mean position: Distance = A = 2 cm
Total Distance=A+A+A+A=4A
Now, substituting the value of amplitude (A = 2 cm):
Total Distance=4×2 cm=8 cm
The distance traveled by the particle in one time period is 8 cm.
The distance traveled by the particle in one time period is 8 cm.
Topper's Solved these Questions
Similar Questions
The velocity of a particle varies with time as per the figure shown. The distance travelled by the particle in 10 seconds is ?(m/s)
View SolutionThe variation of velocity of particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4th second is
View Solution
Knowledge Check
A particle executive simple harmonic motion with an amplitude 'A'. The distance travelled by the particle in one time period is
Azero,BAC2A,D4AThe variation of velocity of a particle moving along straight line is shown in the figure. The distance travelled by the particle in 4 s is
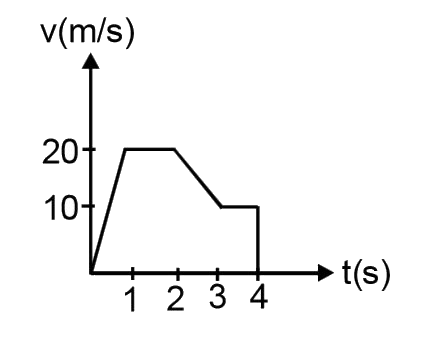 A25mB30mC55mD60m
A25mB30mC55mD60mThe motion of a particle is described by the equation at u=at.The distance travelled by the particle in the first 4 seconds
A4aB12aC6aD8a
The variation of velocity of particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4th second is?
View SolutionThe variation of velocity of a particle moving along a straight line is as shown in the figure given below. The distance travelled by the particle in 5 s is
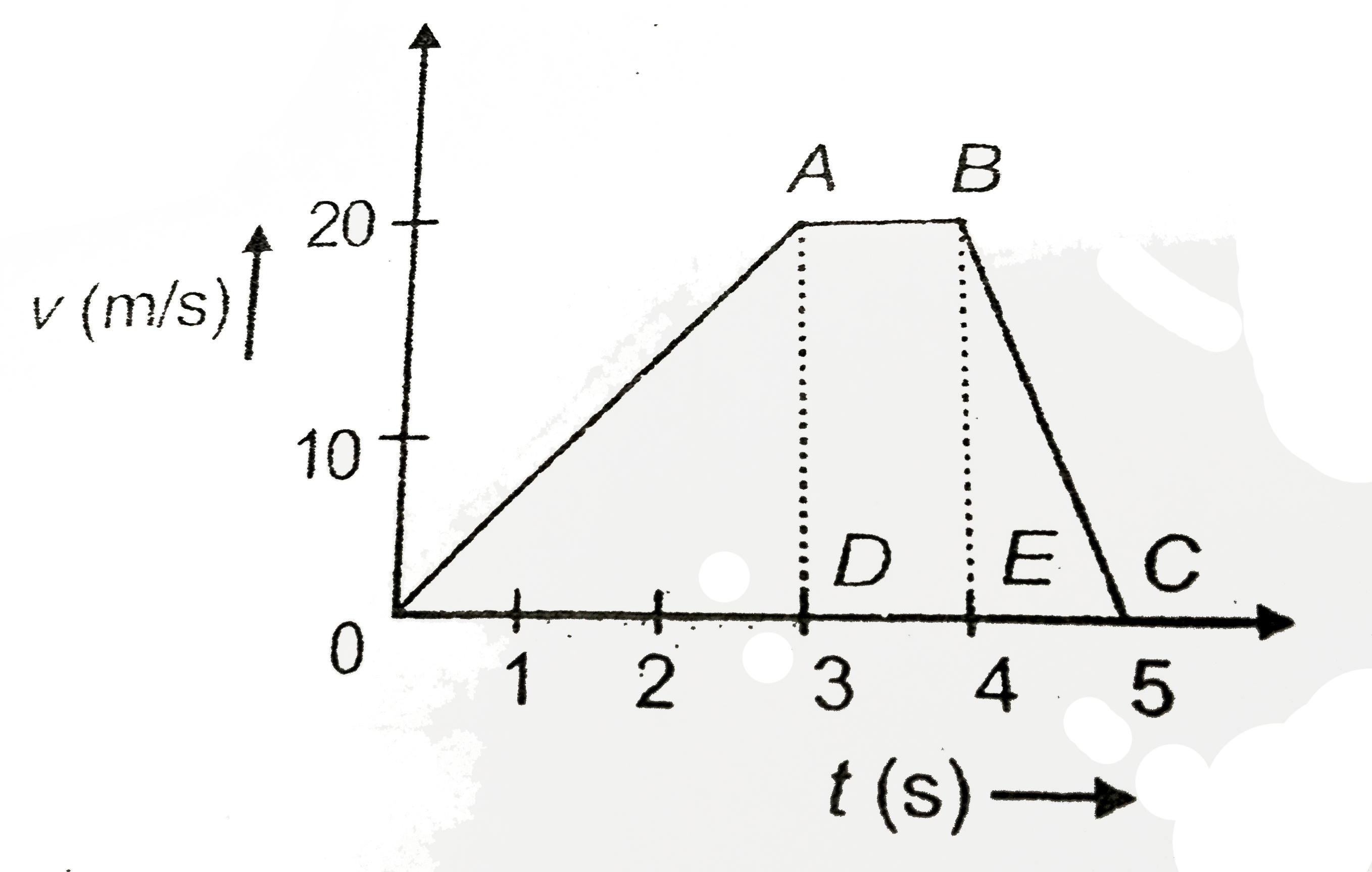
View SolutionThe acceleration of a particle is increasing linearly with time t as bt .The particle starts from the origin with an initial velocity v_(0) The distance travelled by the particle in time t will be
View SolutionThe variation of velocity of a particle with time moving along a straight line is illustrated in the following figure. The distance travelled by the particle in four seconds is.
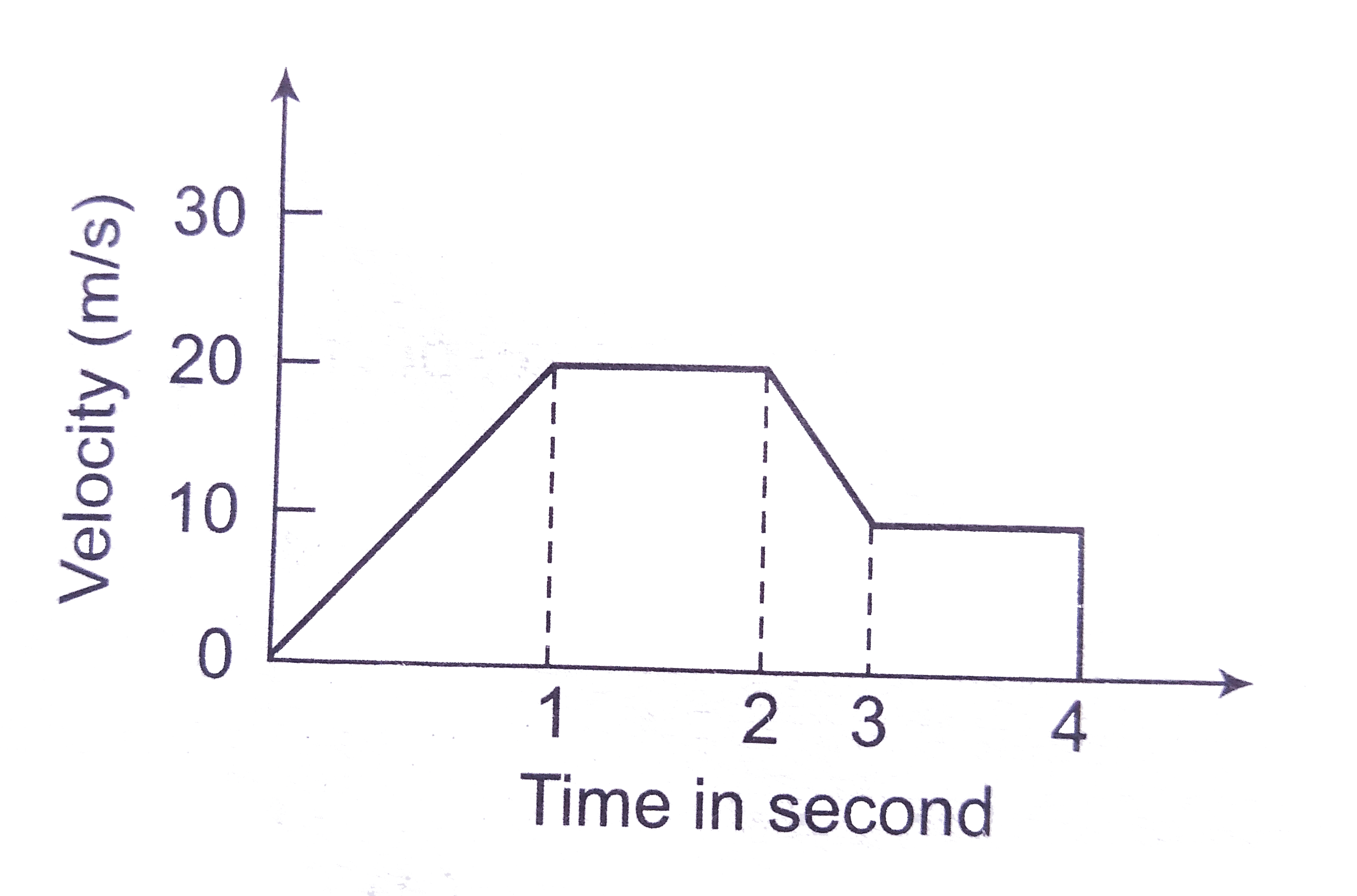
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
View Solution
