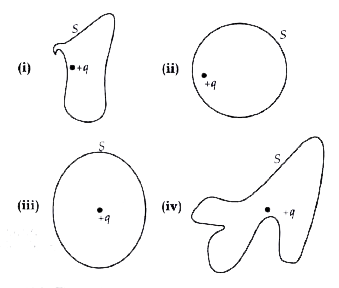The electric flux through a chlosed surface area S enclosing charge Q is ϕ. If the surface area is doubled, then the flux is
2ϕ
ϕ/2
ϕ/4
ϕ
The correct Answer is:D
To solve the problem, we need to understand the relationship between electric flux, charge, and the area of the surface. We will use Gauss's law, which states that the electric flux (Φ) through a closed surface is directly proportional to the charge (Q) enclosed by that surface.
1. Understanding Electric Flux:
The electric flux (Φ) through a closed surface is given by Gauss's law:
Φ=Qenclosedϵ0
where Qenclosed is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
2. Initial Conditions:
We are given that the electric flux through a closed surface area S enclosing charge Q is Φ. Thus, we can write:
Φ=Qϵ0
3. Doubling the Surface Area:
Now, we are told that the surface area is doubled. However, it is important to note that the electric flux depends only on the charge enclosed and not on the area of the surface itself.
4. Charge Enclosed:
Since the charge Q remains the same when we double the surface area, the enclosed charge does not change. Therefore, we still have:
Qenclosed=Q
5. Calculating New Flux:
The electric flux through the new surface area (which is double the original) can still be calculated using Gauss's law:
Φ′=Qenclosedϵ0=Qϵ0
Since Qenclosed=Q, we find that:
Φ′=Φ
6. Conclusion:
The electric flux remains the same, even after doubling the surface area. Therefore, the new flux is:
Φ′=Φ
Final Answer:
The electric flux through the closed surface after doubling the surface area remains Φ.
---
The electric flux (Φ) through a closed surface is given by Gauss's law:
Φ=Qenclosedϵ0
where Qenclosed is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
We are given that the electric flux through a closed surface area S enclosing charge Q is Φ. Thus, we can write:
Φ=Qϵ0
Now, we are told that the surface area is doubled. However, it is important to note that the electric flux depends only on the charge enclosed and not on the area of the surface itself.
Since the charge Q remains the same when we double the surface area, the enclosed charge does not change. Therefore, we still have:
Qenclosed=Q
The electric flux through the new surface area (which is double the original) can still be calculated using Gauss's law:
Φ′=Qenclosedϵ0=Qϵ0
Since Qenclosed=Q, we find that:
Φ′=Φ
The electric flux remains the same, even after doubling the surface area. Therefore, the new flux is:
Φ′=Φ
The electric flux through the closed surface after doubling the surface area remains Φ.
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE EXERCISE (Exercise 2 (MISCELLANEOUS PROBLEMS))47videos
ELECTROSTATICS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - MHT CET Corner29videos
ELECTROSTATICS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - MHT CET Corner29videos
ELECTROSTATICS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTRONS AND PROTONSEXERCISE - MHT CET CORNER19videos
ELECTRONS AND PROTONS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FORCEEXERCISE - Exercise 2 (Miscellaneous Problems)19videos
FORCE
Similar Questions
Knowledge Check
- Question 1 - Select One
The electric flux through a closed surface area S enclosing charge Q is ϕ If the surface area is doubled, then the flux is
A2ϕBϕ/2Cϕ/4Dϕ - Question 2 - Select One
The electric flux through the surface
 Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.
Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures. - Question 3 - Select One
The electric flux through the surface
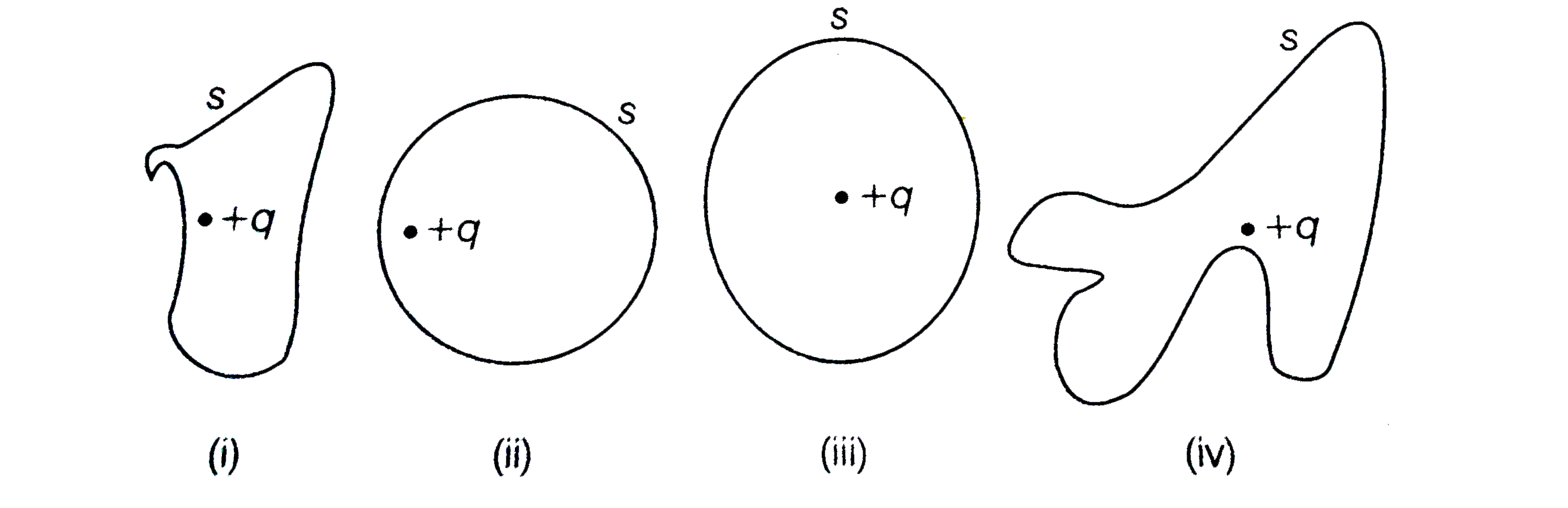 Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.
Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.
The net flux passing through a closed surface enclosing unit charge is
View SolutionIf electric flux passing through a close surface is zero then :-
View SolutionIf the flux of the electric field through a closed surface is zero,
View SolutionElectric flux through a cube with charge q inside is
View SolutionAnswer questions on the basis of your understanding of the following paragraph and the related studied concept.
Electric flux, in general , through any surface is defined as per relation:
ϕE=∫→E.→ds , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface ∮E=∮→E.→ds. it is customary to take the outward normal as positive in this case.
A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ∈0.Mathematically ∮→E.→ds=1∈0[qen] , where qcn is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
A charge q is enclosed by a Gaussian spherical surface of raidus R. If the radius is doubled then the electric flux will.View Solution