The electric flux through a hemispherical surface of radius R placed in a uniform electric field E parallel to the axis of the circular plane is
(2πR)E
(πR2)E
(43πR3)E
(23πR3)E
The correct Answer is:B
To find the electric flux through a hemispherical surface of radius R placed in a uniform electric field E that is parallel to the axis of the circular plane, we can follow these steps:
1. Understanding Electric Flux:
Electric flux (Φ) is defined as the integral of the electric field (E) over a surface area (A):
Φ=∫E⋅dA
2. Identifying the Geometry:
We have a hemispherical surface with a flat circular base. The electric field E is uniform and directed parallel to the axis of the circular base.
3. Calculating the Flux through the Hemispherical Surface:
The electric field is constant, so we can take it out of the integral. The area vector dA for the hemispherical surface points outward, and the angle θ between E and dA varies across the surface.
4. Using Symmetry:
The electric field contributes to the flux through the curved surface of the hemisphere. The contribution to the flux through the flat circular base is zero since the electric field is parallel to the base (angle θ=90∘, cos(90∘)=0).
5. Calculating the Area of the Hemisphere:
The surface area of the hemispherical part is given by:
Ahemisphere=2πR2
6. Calculating the Flux through the Curved Surface:
For the curved surface, we consider the average angle θ between the electric field and the area vector. The average value of cos(θ) over the hemisphere can be shown to be 12.
Therefore, the electric flux through the hemispherical surface can be calculated as:
Φ=E⋅Ahemisphere⋅average(cos(θ))=E⋅(2πR2)⋅12
Φ=E⋅πR2
7. Final Result:
Thus, the electric flux through the hemispherical surface is:
Φ=πR2E
Electric flux (Φ) is defined as the integral of the electric field (E) over a surface area (A):
Φ=∫E⋅dA
We have a hemispherical surface with a flat circular base. The electric field E is uniform and directed parallel to the axis of the circular base.
The electric field is constant, so we can take it out of the integral. The area vector dA for the hemispherical surface points outward, and the angle θ between E and dA varies across the surface.
The electric field contributes to the flux through the curved surface of the hemisphere. The contribution to the flux through the flat circular base is zero since the electric field is parallel to the base (angle θ=90∘, cos(90∘)=0).
The surface area of the hemispherical part is given by:
Ahemisphere=2πR2
For the curved surface, we consider the average angle θ between the electric field and the area vector. The average value of cos(θ) over the hemisphere can be shown to be 12.
Φ=E⋅Ahemisphere⋅average(cos(θ))=E⋅(2πR2)⋅12
Φ=E⋅πR2
Thus, the electric flux through the hemispherical surface is:
Φ=πR2E
Topper's Solved these Questions
Similar Questions
Knowledge Check
The electric flux through the surface
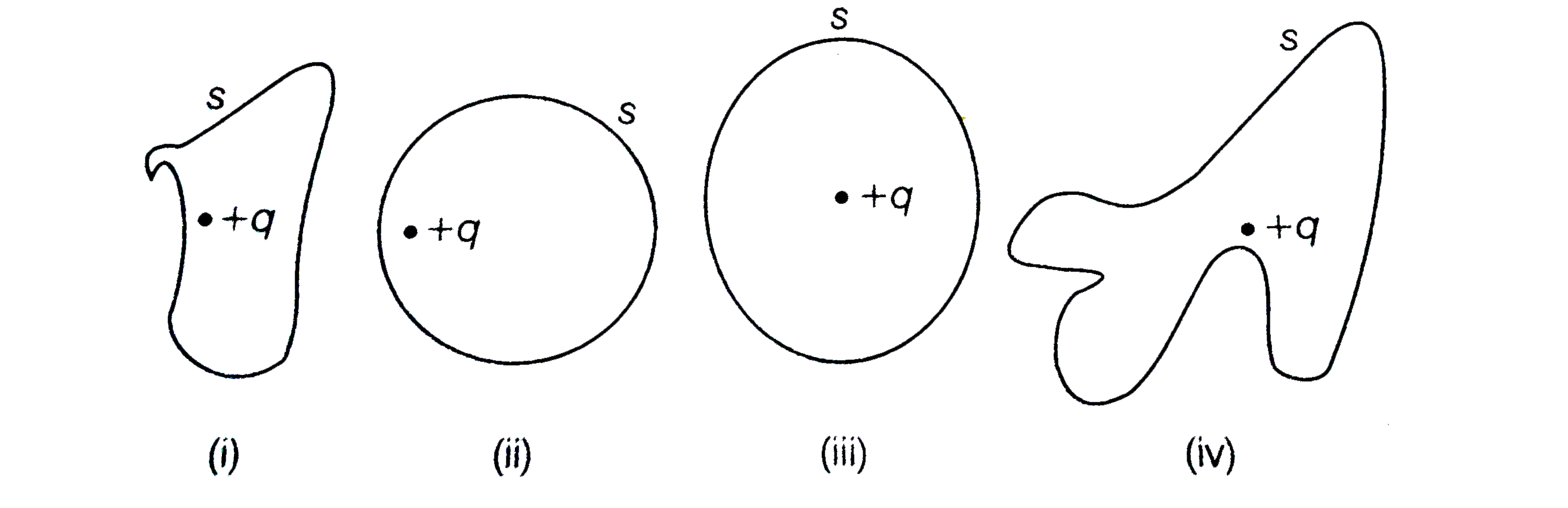 Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.
Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.The electric flux through the surface
 Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.
Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.The length and radius of a cylinder are L and R respectively. The total flux for the surface of the cylinder, when it is placed in a uniform electric field E parallel to the axis of the cylinder is
AzeroB2πR2EC2πR2EDπR2E
If a hemispherical body is placed in a uniform electric field E then the flux linked with the curved surface is E B
View SolutionConsider a cylindrical surface of radius R and length l in a uniform electric field E. Compute the electric flux if the axis of the cylinder is parallel to the field direction.
View SolutionCalculate the elecric flux though a hemisphere of radius R . The electric field E is unfrom and is (a) parallel,(b) perpendicular to axis of the hemisphere.
View SolutionA hemispherical body of radius R is placed in a uniform electric field E. If the field E is parallel to the base of the hemisphere the flux linked with it is
View SolutionA hemispherical bowl of radius r is placed in uniform electric field E . The electric flux passing through the bowl is
View Solution