The electrical resistance in ohms of a certain thermometer varies with temperature ac cording to the approximate law: $R = R_{0} [1 + α (T - T_{0})]$
The resistances is $101.6 Ω$ at the triple-point of water $273.16 K$ , and $165.5 Ω$ at the normal melting point of lead $(600.5 K)$ . What is the temperature when the resistance is $123.4 Ω$ ?

Video Solution

Text Solution

Verified by Experts

For water the triple-point is $T_{0} = 273.16 K$
$R_{0} = 101.6 Ω$ Case(i): $T_{0} = (600.5 K), R_{0} = 165.5 Ω$
As $R = R_{0} (1 + α (T - T_{0}))$
$∴ 165.5 = 101.6 [1 + α (600.5 - 273.16)]$
$\frac{165.5 - 101.6}{101.6 \times (600.5 - 273.16)} = α$
$\frac{63.9}{101.6 \times 327.34} = α$
$\Rightarrow α = 0.0019$
Case (ii) $R = 123.4 Ω, T = ?$
$R = R_{0} (1 + α (T - T_{0}))$
$123.4 = 101.6 [1 + 0.0019 (T - 273.16)]$
$\frac{123.4 - 101.6}{101.6 \times 0.0019} = T - 273.16$
$= 112.9 + 273.16 = T$
T = 386.06 K

The resistance t R of a conductor varies with temperature t as shown in the figure. If the variation is represented by $R_{t} = R_{0} [1 + α t + β t^{2}]$ , then

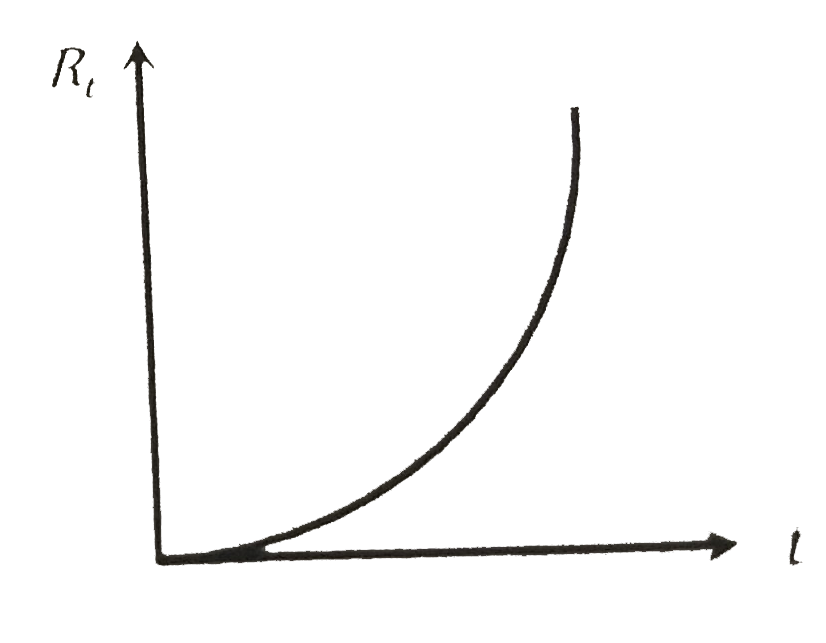A $α$ and $β$ are both negative
B $α$ and $β$ are both positive
C $α$ is positive and $β$ is negative
D $α$ is negative and $β$ are positive
The temperature coefficient of resistance of wire is ${0.001259}^{\circ} C^{- 1}$ . If resistance is $1 Ω$ at 300 K, then $2 Ω$ will be at:
A1400 K
B1100 K
C1127 J
D1154 K
Choose the most appropriate option.
The resistance R of a conductor varies with temperature t as shown in figure. If the variation is represented by $R_{t} = R_{0} (1 + α t + β t^{2})$ .

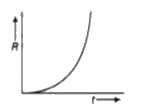
Then
A $α and β$ bothe negative
B $α$ is positive and $β$ is negative
C $α and β$ both are positive
D $α$ is negative and $β$ is negative