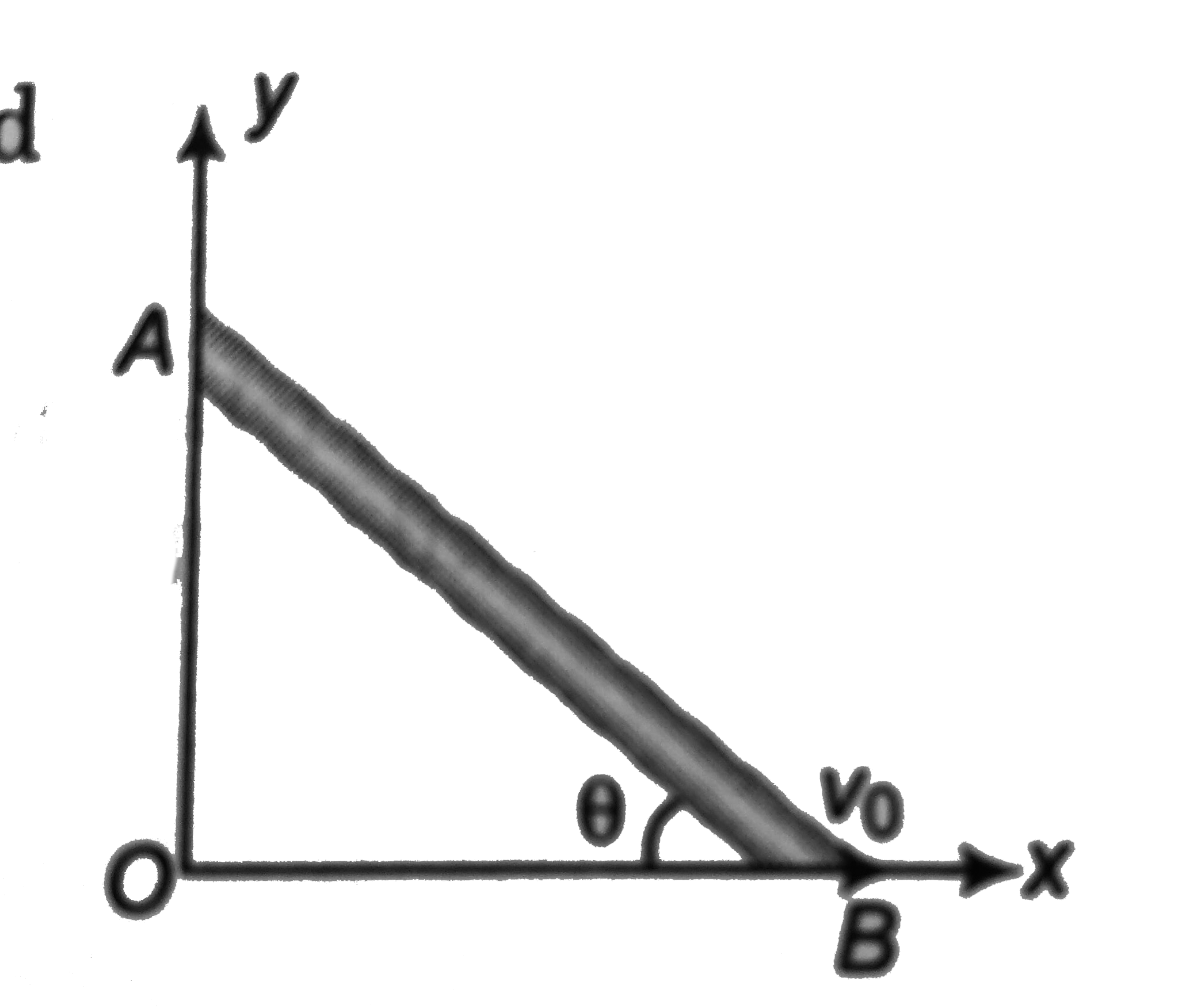
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity vv as shown. The length of the rod is l.
At θ=37∘ velocity of end A is 43v0 downwards
At θ=37∘ angular velocity of rod is 5v03l
Angular velocity of rod is constant
velocity of end A is constant.

Velocity component along AB=0
∴v0cosθ=vsinθ
or v=v0cotθ=f1(θ)
at θ=37∘,v=43v0
ω=relative velocity ⊥to ABl
=v0sinθ+vcosθl=f2(θ)
=(v0)(3/5)+(4/3v0)(4/5)l=5v03l
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Subjective
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity v0 as shown. The length of the rod is l. At the instant when θ=37∘, the angular velocity of the rod is pqv0l. Find (p+q).
'(##CEN_KSR_PHY_JEE_C07_009_Q05##) '
View SolutionA conducting rod AB of lemgth 2 l moves through a uniform magnetic field B. The rod makes an angle θ with the vertical while it falls with a uniform linear velocity v. The potential difference between the two ends of the rod is Bv2l .

View Solution
Knowledge Check
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity v0 as shown. The length of the rod is l. At the instant when θ=37∘
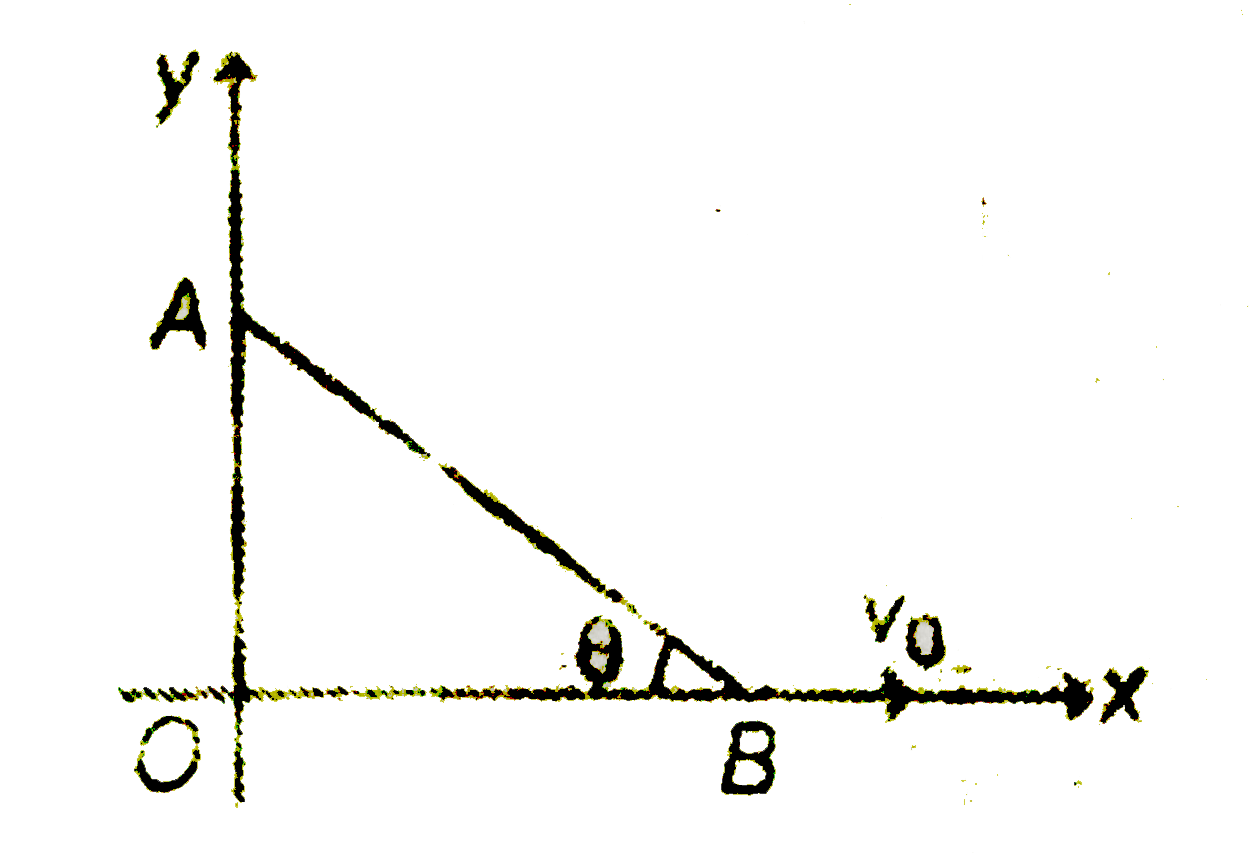 Avelocity of end A is 43v0 downwardsBangular velocity of rod is 53v0lCangular velocity of rod is constantDvelocity of end A is constant
Avelocity of end A is 43v0 downwardsBangular velocity of rod is 53v0lCangular velocity of rod is constantDvelocity of end A is constantEnd A of a rod AB is being pulled on the floor with a constant velocity v0 as shown. Taking the length of the rod as l, at an instant when the rod makes an angle 37∘ with the horizontal, calculate
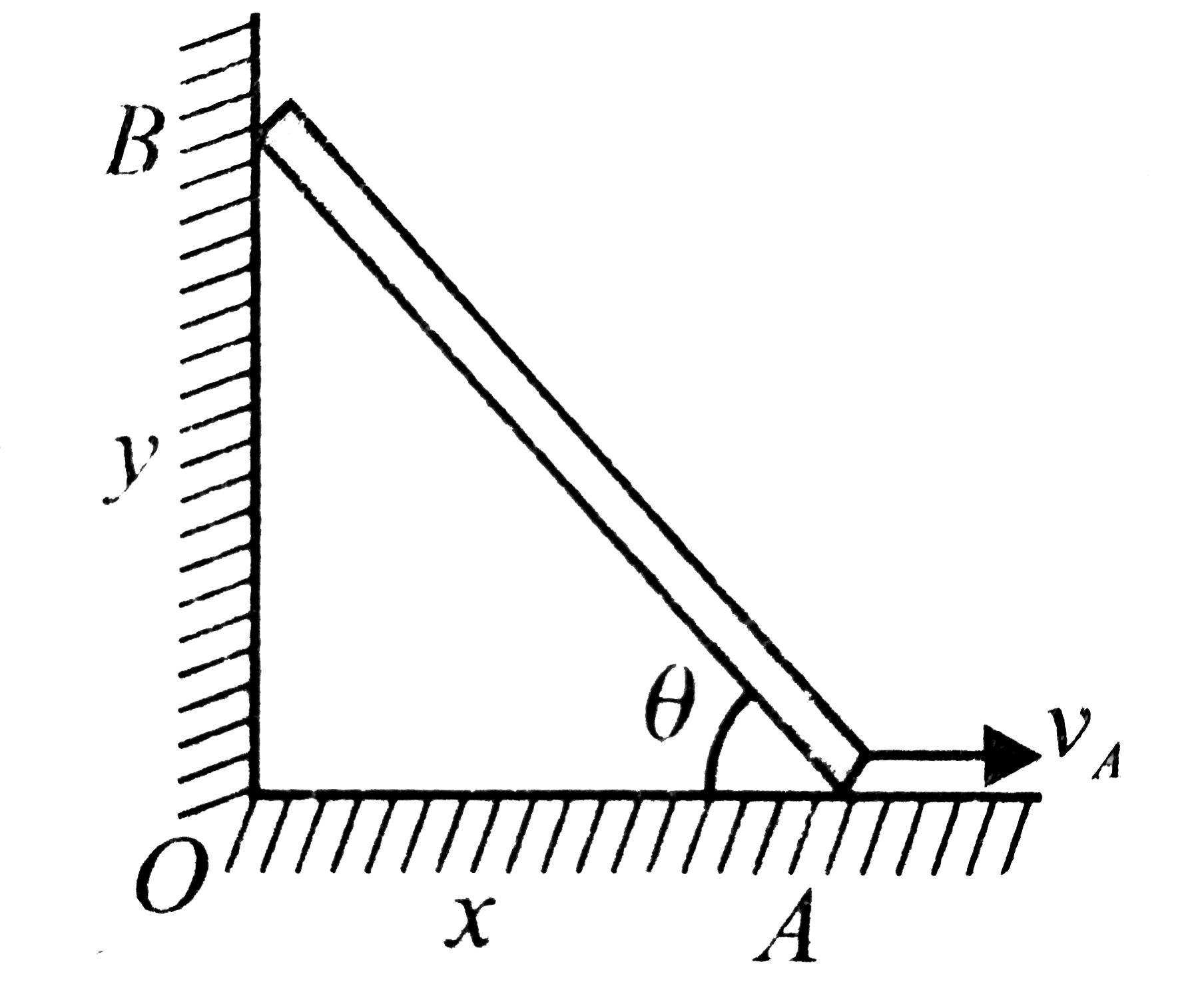
the velocity of the CM of the rodA57v0 at tan−143 below horizontalB57v0 at tan−134 below horizontalC56v0 at tan−134 below horizontalD56v0 at tan−143 below horizontalIn the arrangement shown, end A of light intextensible string is pulled with constant velocity v. the velocity of block B is
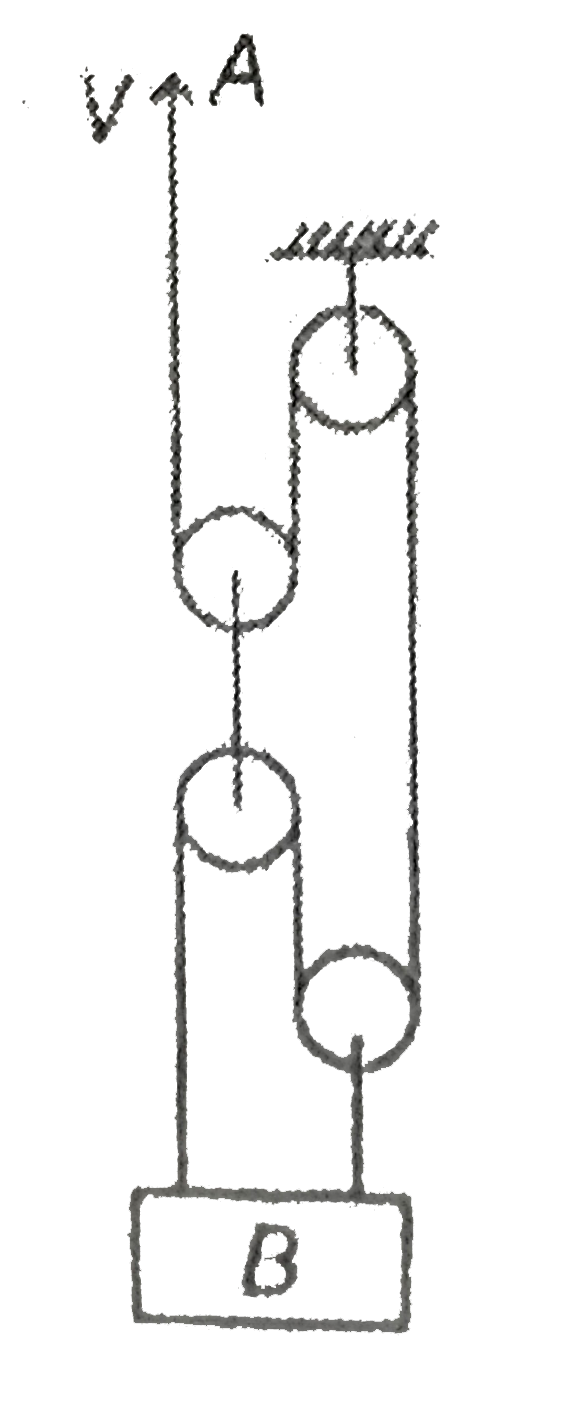 AV/2BvCv/3D3v
AV/2BvCv/3D3v
A rod of length 'l' is inclined at an angle 'theta' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1 what is the velocity of end B at the instant when rod makes 'theta' angle with the horizontal .
View SolutionFigure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

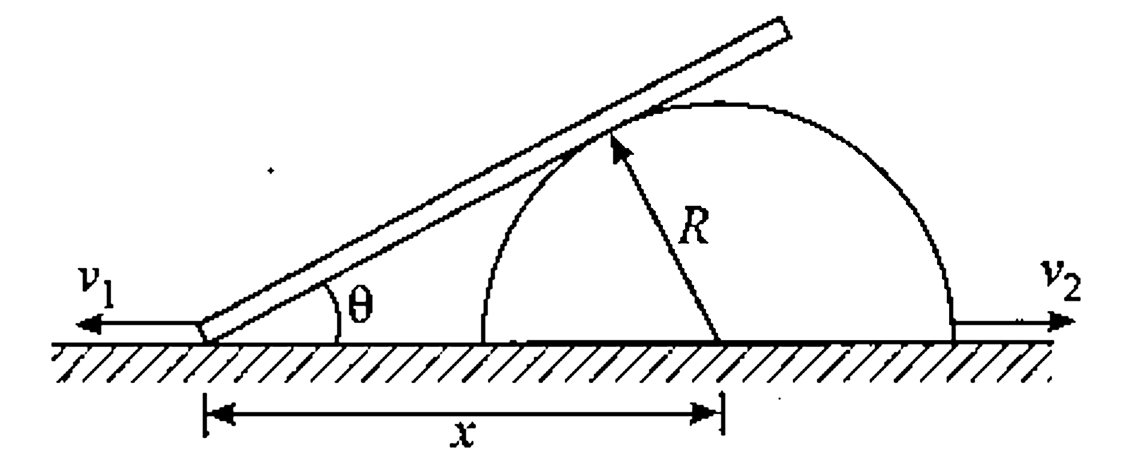
View SolutionFigure-1.52 showns a hemisphere and a supported rod. Hemisphere is moving in right direction with a uniform velocity v2 and the end of rod which is in contact with ground is moving in left direction with a velocity v1. Find the rate at which the angle θ is changing in terms of v1,v2, R and θ.
View SolutionA rod length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At a certain instant of time, when the rod makes an angle θ with horizontal the velocity of COM of the rod is v0. The velocity of the end of the rod in contact with the surface at that instant is:
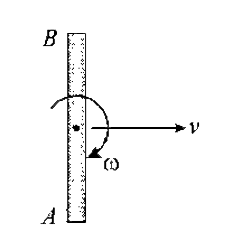
View SolutionA uniform rod AB of length l rotating with an angular velocity ω while its centre moves with a linear velocity v=ωl6 If the end A of the rod is suddenly fixed, the angular velocity of
View Solution
